Função do Verde

Generalmente falando, a função de Green é um kernel integral que pode ser usado para resolver equações diferenciais de um grande número de famílias, incluindo exemplos mais simples como equações diferenciais comuns com condições de valor inicial ou limite, bem como exemplos mais difíceis como equações diferenciais parciais não homogêneas (EPP) com condições de limite. Importante por uma série de razões, as funções de Green permitem interpretações visuais das ações associadas a uma fonte de força ou a uma carga concentrada em um ponto (Qin 2014), tornando-as assim particularmente úteis em áreas da matemática aplicada. Em particular, os métodos das funções de Green são amplamente utilizados em, por exemplo física, e engenharia.

Mais precisamente, dado um operador diferencial linear actuando na recolha de distribuições sobre um subconjunto de algum espaço euclidiano , função de um Verde no ponto correspondente a é qualquer solução de

(1)

where denota a função delta. A motivação para definir tal função é generalizada, mas multiplicando a identidade acima por uma função e integrando com respeito a rendimentos

(2)

O lado direito reduz apenas para devido às propriedades da função delta, e porque é um operador linear agindo apenas em e não em , o lado esquerdo pode ser reescrito como

(3)

Esta redução é particularmente útil ao resolver para em equações diferenciais da forma

(4)

Onde a aritmética acima confirma que

>

(5)

e daí que tem a forma integral específica

>

(6)

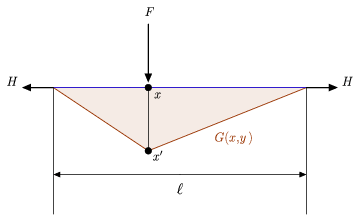
A figura acima ilustra tanto a interpretação física intuitiva da função de um Verde como uma equação diferencial relativamente simples associada com a qual se pode comparar a definição acima (Hartmann 2013). Em particular, mostra uma corda esticada de comprimento suspensa entre duas paredes, mantida no lugar por uma força horizontal idêntica aplicada em cada uma de suas extremidades, e uma carga lateral colocada em algum ponto interior sobre a corda. Que seja o ponto correspondente a na corda desviada, suponha que a força descendente seja constante, digamos , e que denote a deflexão da corda. Correspondendo a este sistema físico está a equação diferencial

(7)

for com , um sistema cuja simplicidade permite tanto a sua solução como a sua função Verde a ser escrita explicitamente:

(8)

e

>

(9)

respectivamente. Como demonstrado na figura acima, a corda deslocada tem o formato linear de peça dado por acima, confirmando assim a alegação de que a função do Verde associada a este sistema representa a acção da corda horizontal correspondente à aplicação de uma força .

A função do Verde tomando um par de argumentos é por vezes referida como uma função de dois pontos do Verde. Isto está em contraste com as funções de vários pontos verdes, que são de particular importância na área da teoria de muitos corpos.

Como um exemplo elementar de uma função de dois pontos como definida acima, considere o problema de determinar o potencial gerado por uma distribuição de carga cuja densidade de carga é , onde as aplicações da equação de Poisson e da lei de Coulomb ao potencial em produzido por cada elemento de carga produz uma solução

(10) >

>

que se mantém, sob certas condições, sobre a região onde . Como o lado direito pode ser visto como um operador integral convertendo em , pode-se reescrever esta solução em termos da função de um Verde tendo a forma

(11)

onde a solução pode ser reescrita:

(12)

(Arfken 2012).

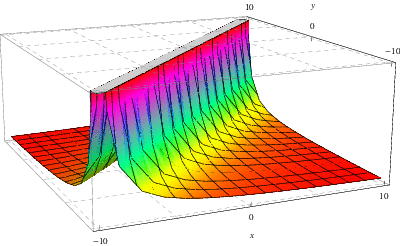
A figura acima mostra a função do Verde associada à solução do – equação discutida acima onde aqui, e , respectivamente , é plotado no eixo -, respectivamente -.

Uma lista algo abrangente das funções de Green correspondente a várias equações diferenciais é mantida online por Kevin Cole (Cole 2000).

De acordo com a multiplicidade da literatura escrita sobre as funções de Green, podem surgir várias notações e definições diferentes, algumas das quais são topicamente diferentes das acima mencionadas mas que, em geral, não afectam as propriedades importantes dos resultados. Como o exemplo acima ilustra, por exemplo, alguns autores preferem denotar as variáveis e em termos de vetores e para enfatizar o fato de que são elementos de para alguns que podem ser maiores que 1 (Arfken 1985). É também relativamente comum ver a definição com um sinal negativo de modo que é definido como sendo a função para a qual

(13)

mas devido ao facto desta consideração puramente física não ter qualquer efeito sobre a matemática subjacente, este ponto de vista é geralmente ignorado. Sabe-se também que existem várias outras notações para a função de um Verde, algumas das quais incluem o uso de uma minúscula no lugar de (Stakgold 1979), bem como a inclusão de uma linha vertical em vez de uma vírgula, por exemplo, (Duffy 2001).

Em outras instâncias, a literatura apresenta definições que estão intimamente ligadas aos contextos em que são apresentadas. Por exemplo, alguns autores definem as funções de Green como sendo funções que satisfazem um determinado conjunto de condições, por exemplo, existência num tipo especial de domínio, associação com um operador diferencial muito particular , ou satisfação de um conjunto preciso de condições de fronteira. Um dos exemplos mais comuns pode ser encontrado em notas, por exemplo, por Speck, onde a função de um Verde é definida para satisfazer para pontos e para todos os pontos deitado no limite de (Speck 2011). Esta definição particular apresenta um núcleo integral correspondente à solução de uma equação generalizada de Poisson e, portanto, enfrentaria limitações óbvias ao ser adaptada a um cenário mais geral. Por outro lado, tais exemplos não estão sem os seus benefícios. No caso do exemplo generalizado de Poisson acima, por exemplo, cada uma dessas funções de Green pode ser dividida de modo que

(14)

where e para o Laplacian regular (Hartman 2013). Em tais situações, é conhecida como a solução fundamental da equação diferencial subjacente e é conhecida como sua solução regular; como tal, e são algumas vezes chamadas de partes fundamental e regular de , respectivamente.

Propriedades fundamentaiseverais de uma função geral do Verde seguem imediatamente (ou quase) da sua definição e transitam para todas as instâncias particulares. Por exemplo, se o kernel do operador é não trivial, então pode haver várias funções de Green associadas a um único operador; como resultado, deve-se ter cautela ao se referir à “função” de Green. As funções de Green satisfazem uma simetria adjunta em seus dois argumentos de modo que

(15)

Em qualquer lugar aqui, está definido para ser a solução da equação

(16)

Aqui, é o adjunto de . Um corolário imediato deste fato é que para operadores auto-ajustados , é simétrico:

(17)

Esta identidade é frequentemente chamada de princípio da reciprocidade e diz, em termos físicos, que a resposta em causada por uma fonte unitária em é a mesma que a resposta em devido a uma força unitária em (Stakgold 1979).

A propriedade essencial de qualquer função de Green é que ela fornece uma maneira de descrever a resposta de uma solução de equação diferencial arbitrária a algum tipo de termo de fonte na presença de algum número de condições limite (Arfken et al. 2012). Alguns autores consideram uma função de Green para servir aproximadamente um papel análogo na teoria das equações diferenciais parciais como as séries de Fourier na solução de equações diferenciais ordinárias (Mikula e Kos 2006).

Para cenários mais abstratos, existe uma série de conceitos que servem como análogos específicos do contexto para a noção de função de Green. Por exemplo, na análise funcional, é frequentemente útil considerar a chamada função generalizada de Green que tem muitas propriedades análogas quando integrada de forma abstrata contra funções em vez de funções. Na verdade, tais generalizações produziram um ramo inteiramente análogo da análise teórica de PDE e são elas próprias o foco de uma grande quantidade de pesquisas.