Filtragem Bilinear e Interpolação Bilinear

Dê uma olhada na foto abaixo. É possível calcular os valores nos pontos A,B e C?

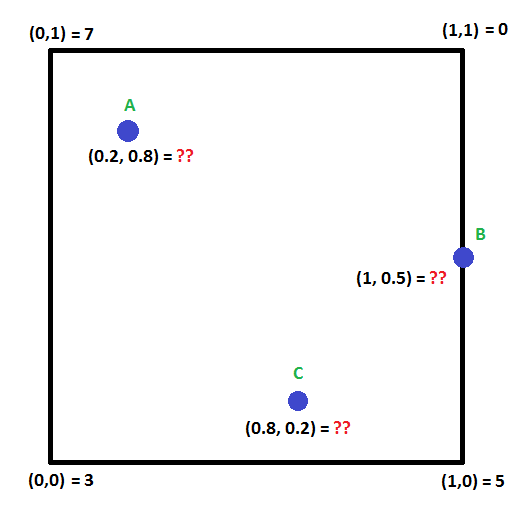
Há uma técnica para fazer isto chamada interpolação bilinear que estende a ideia de interpolação linear em duas dimensões.

Para calcular a interpolação bilinear, basta fazer a interpolação linear num eixo, e depois no outro.

Cheque estes exemplos:

Ponto A
Ponto A tem uma coordenada de (0,2,0,8). Vamos começar com o eixo X.

Primeiro, vamos fazer interpolação através do topo do quadrado no eixo X. Isso significa que precisamos ir de 0,2 (20%) do caminho de 7 a 0. Essa 0,2 é a nossa coordenada do eixo X. Para calcular isso:
7 + (0-7) * 0,2 = 5,6

Próximo, faremos a interpolação através da parte inferior do quadrado no eixo X. Tão semelhante ao acima, iremos 0,2 (20%) do caminho de 3 a 5. Para calcular isso:
3 + (5-3) * 0,2 = 3,4

Agora interpolamos através do nosso eixo X, precisamos interpolar através do nosso eixo Y. Agora vamos 0,8 (80%) do caminho do nosso valor inferior (o valor de Y = 0), para o nosso valor superior (o valor de Y = 1). O valor inferior é a interpolação inferior que fizemos (3,4) e o valor superior é a interpolação superior que fizemos (5,6).

Então, precisamos ir 0,8 (80%) do caminho de 3,4 a 5,6. Para calcular isso:
3,4 + (5,6 – 3,4) * 0,8 = 5,16

Então, o valor no ponto A é 5,16. A imagem abaixo deve ajudar a explicar visualmente o processo pelo qual passamos.

Ponto B

Ponto B tem uma coordenada de (1.0,0.5).

Vamos começar com a interpolação do eixo X novamente (embora você poderia facilmente começar com Y primeiro se quisesse! Você acabaria com o mesmo resultado).

Fazendo a interpolação do eixo X através do topo, precisamos ir 1,0 (100%) do caminho de 7 a 0. Tenho certeza que você pode adivinhar qual é a resposta, mas aqui é calculado:
7 + (0-7) * 1,0 = 0

Simplesmente, vamos fazer a interpolação do eixo X através do fundo. Precisamos ir 1,0 (100%) do caminho de 3 a 5,
3 + (5-3) * 1,0 = 5

Próximo vem a interpolação do eixo Y. Precisamos ir 0,5 (50%) do caminho de 5 a 0,
5 + (0-5) * 0,5 = 2,5

Aqui vamos nós, o valor no ponto B é 2,5. Isso também deve fazer sentido ao olhar para o diagrama. É basicamente uma interpolação linear 1d entre 5 e 0, e está a meio caminho entre eles, portanto intuitivamente, a resposta 2,5 deve fazer sentido.

Ponto C

Ponto C tem uma coordenada de (0,8,0,2).

Até novamente, vamos fazer a interpolação do eixo X através do topo da caixa. Precisamos de ir 0,8 (80%) do caminho de 7 a 0,
7 + (0-7) * 0,8 = 1,4

Então, precisamos de fazer a interpolação do eixo X através da parte inferior da caixa. Precisamos ir 0,8 (80%) do caminho de 3 a 5,
3 + (5-3) * 0,8 = 4,6

Próxima interpolação do eixo y. Precisamos ir 0,2 (20%) de 4,6 para 1,4,
4,6 + (1,4-4,6) * 0,2 = 3,96

O valor do ponto C é 3.96

Filtragem bilinear

Embora a interpolação bilinear seja útil se você tiver uma grade de dados que você quer interpolar valores dentro (como um campo de altura que representa o terreno?!), onde isso realmente brilha no desenvolvimento do jogo é na filtragem de textura bilinear.

Basicamente, quando você tem uma coordenada de textura que não se alinha perfeitamente com o centro de um pixel na textura (porque há um resto), ele usa a parte fracional da coordenada dentro desse pixel para fazer interpolação bilinear entre os 4 pixels envolvidos para chegar à cor final do pixel. Ele faz interpolação bilinear em cada um dos canais: Vermelho, Verde, Azul e Alfa.

O resultado final é muito bom! Confira a imagem abaixo para vê-la em ação em uma textura que estamos ampliando demais. O lado esquerdo usa filtragem bilinear, enquanto o lado direito não, e mostra apenas o pixel mais próximo.

Consequentemente, a filtragem de textura bilinear tem que fazer uma leitura de 4 pixels para poder interpolar entre eles, ao invés de uma leitura de um único pixel como quando se faz uma amostragem de pixels mais próxima. Mais leituras de pixels = mais overhead, e não tão baratas (computacionalmente) para usar.

Links

Para algumas pessoas que estão lendo isto, esta informação é bastante básica e você pode estar se perguntando porque eu me dei ao trabalho de escrever sobre isto. Olhe para o próximo post para algo meio bizarro em relação à filtragem bilinear. Isto foi necessário como um trampolim para a próxima coisa que eu quero mostrar a vocês 😛

Wikipedia: Interpolação Linear

Wikipedia: Interpolação Bilinear

Wikipédia: Filtragem Bilinear

O Lado Negro da Filtragem Bilinear

Cheque estes links para mais informações sobre algumas falhas (e algumas soluções) de amostragem bilinear baseada em hardware:
iq: interpolação de hardware
iq: interpolação de textura melhorada