Amostragem de Gibbs

Like other MCMC methods, o amostrador Gibbs constrói uma Markov Chain cujos valores convergem para uma distribuição-alvo. A amostragem de Gibbs é de facto um caso específico do algoritmo Metropolis-Hastings em que as propostas são sempre aceites.

Para elaborar, suponha que queria amostrar uma distribuição de probabilidade multivariada.

Nota: Uma distribuição de probabilidade multivariada é uma função de múltiplas variáveis (isto é, uma distribuição de probabilidade multivariada é uma função de múltiplas variáveis). 2 distribuição normal dimensional).

Não sabemos como amostrar a partir destas últimas directamente. No entanto, devido a alguma conveniência matemática ou talvez apenas pura sorte, nós conhecemos as probabilidades condicionais.

>

É aqui que entra a amostragem de Gibbs. A amostragem de Gibbs é aplicável quando a distribuição conjunta não é conhecida explicitamente ou é difícil de amostrar diretamente, mas a distribuição condicional de cada variável é conhecida e é mais fácil de amostrar a partir de.

Iniciamos selecionando um valor inicial para as variáveis aleatórias X & Y. Em seguida, amostramos a partir da distribuição condicional de probabilidade de X dado Y = Y⁰ denoted p(X|Y⁰). No próximo passo, amostramos um novo valor de Y condicional em X¹, que acabamos de computar. Repetimos o procedimento para uma iteração adicional de n – 1, alternando entre extrair uma nova amostra da distribuição condicional de probabilidade de X e a distribuição condicional de probabilidade de Y, dado o valor atual da outra variável aleatória.

Vejamos um exemplo. Suponha que tivemos as seguintes distribuições de probabilidade posteriores e condicionais.

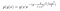
onde g(y) contém os termos que não incluem x, e g(x) contém os que não dependem de y.

Não sabemos o valor de C (constante normalizante). No entanto, nós conhecemos as distribuições de probabilidade condicional. Portanto, podemos usar Gibbs Sampling para aproximar a distribuição posterior.

Nota: As probabilidades condicionais são de fato distribuições normais, e podem ser reescritas da seguinte forma.

Dadas as equações anteriores, procedemos à implementação do algoritmo de Amostragem de Gibbs em Python. Para começar, importamos as seguintes bibliotecas.

import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
sns.set()

Definimos a função para a distribuição posterior (suponha C=1).

f = lambda x, y: np.exp(-(x*x*y*y+x*x+y*y-8*x-8*y)/2.)

Então, plotamos a distribuição de probabilidade.

xx = np.linspace(-1, 8, 100)
yy = np.linspace(-1, 8, 100)
xg,yg = np.meshgrid(xx, yy)
z = f(xg.ravel(), yg.ravel())
z2 = z.reshape(xg.shape)
plt.contourf(xg, yg, z2, cmap='BrBG')

Agora, vamos tentar estimar a distribuição de probabilidade usando Gibbs Amostragem. Como mencionamos anteriormente, as probabilidades condicionais são distribuições normais. Portanto, podemos expressá-las em termos de mu e sigma.

No seguinte bloco de código, definimos funções para mu e sigma, inicializamos nossas variáveis aleatórias X & Y, e definimos N (o número de iterações).

N = 50000
x = np.zeros(N+1)
y = np.zeros(N+1)
x = 1.
y = 6.
sig = lambda z, i: np.sqrt(1./(1.+z*z))
mu = lambda z, i: 4./(1.+z*z)

Passamos pelo algoritmo de amostragem de Gibbs.

for i in range(1, N, 2):
sig_x = sig(y, i-1)
mu_x = mu(y, i-1)
x = np.random.normal(mu_x, sig_x)
y = y
sig_y = sig(x, i)
mu_y = mu(x, i)
y = np.random.normal(mu_y, sig_y)
x = x

Finalmente, plotamos os resultados.

plt.hist(x, bins=50);
plt.hist(y, bins=50);

plt.contourf(xg, yg, z2, alpha=0.8, cmap='BrBG')
plt.plot(x,y, '.', alpha=0.1)
plt.plot(x,y, c='r', alpha=0.3, lw=1)

Como podemos ver, a distribuição de probabilidade obtida usando o algoritmo Gibbs Sampling faz um bom trabalho de aproximação da distribuição alvo.

Conclusão

A Amostragem de Gibbs é um método Monte Carlo Markov Chain que retira iterativamente uma instância da distribuição de cada variável, condicional aos valores atuais das outras variáveis, a fim de estimar distribuições conjuntas complexas. Em contraste com o algoritmo Metropolis-Hastings, aceitamos sempre a proposta. Assim, a amostragem de Gibbs pode ser muito mais eficiente.