9.5 – Identificando Pontos de Dados Influenciais

Nesta seção, aprendemos as duas seguintes medidas para identificar pontos de dados influentes:

• Diferença em Fits (DFFITS)
• Distâncias do cozinheiro

A idéia básica por trás de cada uma destas medidas é a mesma, ou seja, apagar as observações uma de cada vez, cada vez remontando o modelo de regressão nas observações n-1 restantes. Em seguida, comparamos os resultados usando todas as n observações com os resultados com a i-ésima observação eliminada para ver quanta influência a observação tem sobre a análise. Analisado como tal, somos capazes de avaliar o impacto potencial que cada ponto de dados tem na análise de regressão.

Diferença em Fits (DFFITS)

A diferença de ajustes para a observação i, designada DFFITSi, é definida como:

\

Como se pode ver, o numerador mede a diferença nas respostas previstas obtidas quando o i-ésimo ponto de dados é incluído e excluído da análise. O denominador é o desvio padrão estimado da diferença nas respostas previstas. Portanto, a diferença em ajustes quantifica o número de desvios padrão que o valor ajustado muda quando o i-ésimo ponto de dados é omitido.

Uma observação é considerada influente se o valor absoluto de seu valor DFFITS for maior que:

\

onde, como sempre, n = o número de observações e k = o número de termos preditores (ou seja, o número de parâmetros de regressão excluindo a intercepção). É importante ter em mente que esta não é uma regra difícil e rápida, mas sim apenas uma diretriz! Não é difícil encontrar autores diferentes usando uma linha diretriz ligeiramente diferente. Portanto, muitas vezes prefiro uma diretriz muito mais subjetiva, como um ponto de dados é considerado influente se o valor absoluto do seu valor DFFITS se destaca como um polegar dorido dos outros valores DFFITS. É claro que este é um julgamento qualitativo, talvez como deveria ser, já que os outliers pela sua própria natureza são quantidades subjetivas.

Exemplo #2 (novamente). Vamos verificar a diferença na medida de ajuste para este conjunto de dados (influência2.txt):

Regressing y on x and requesting the difference in fits, we obtain the following software output:

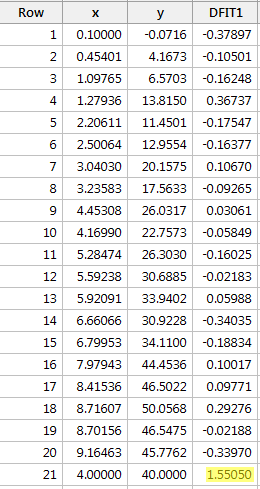
Usando a diretriz objetiva definida acima, consideramos um ponto de dados como sendo influente se o valor absoluto de seus DFFITS for maior que:

\

Apenas um ponto de dados – o vermelho – tem um valor DFFITS cujo valor absoluto (1.55050) é maior que 0,82. Portanto, com base nesta diretriz, consideraríamos o ponto de dados vermelho influente.

Exemplo #3 (novamente). Vamos verificar a diferença na medida de ajuste para este conjunto de dados (influência3.txt):

Regressing y on x e solicitando a diferença em ajustes, obtemos a seguinte saída do software:

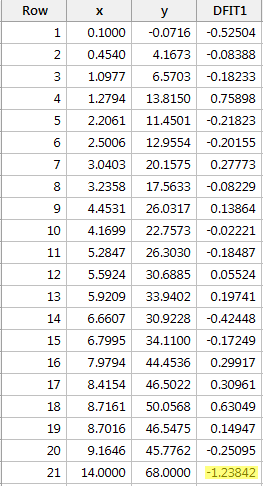
Usando a diretriz objetiva definida acima, consideramos um ponto de dados como sendo influente se o valor absoluto de seus DFFITS for maior que:

Apenas um ponto de dados – o vermelho – tem um valor DFFITS cujo valor absoluto (1.23841) é maior que 0,82. Portanto, com base nesta diretriz, consideraríamos o ponto de dados vermelho influente.

Quando estudamos este conjunto de dados no início desta lição, decidimos que o ponto de dados vermelho não afetou muito a análise de regressão. No entanto, aqui, a diferença na medida de ajuste sugere que ele é realmente influente. O que está a acontecer aqui? Tudo se resume a reconhecer que todas as medidas nesta lição são apenas ferramentas que sinalizam pontos de dados potencialmente influentes para o analista de dados. No final, o analista deve analisar o conjunto de dados duas vezes – uma com e outra sem os pontos de dados sinalizados. Se os pontos de dados alterarem significativamente o resultado da análise de regressão, então o pesquisador deve relatar os resultados de ambas as análises.

Incidentalmente, neste exemplo aqui, se usarmos a diretriz mais subjetiva de se o valor absoluto do valor DFFITS se mantém como um polegar dorido, é provável que não consideremos o ponto de dados vermelho como sendo influente. Afinal, o próximo maior valor de DFFITS (em valor absoluto) é 0,75898. Este valor DFFITS não é muito diferente do valor DFFITS do nosso ponto de dados “influente”.

Exemplo #4 (novamente). Vamos verificar a diferença na medida de ajuste para este conjunto de dados (influência4.txt):

Regressing y on x and requesting the difference in fits, we obtain the following software output:

>

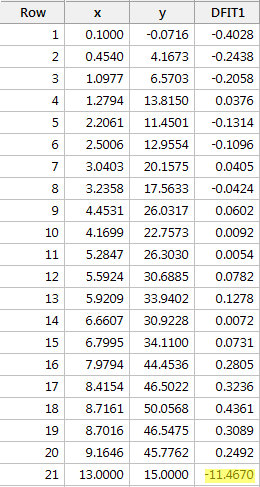
Usando a diretriz objetiva definida acima, novamente consideramos um ponto de dados como sendo influente se o valor absoluto de seus DFFITS for maior que:

O que você acha? Algum dos valores dos DFFITS fica de fora como um polegar dorido? Errr – o valor dos DFFITS do ponto de dados vermelho (-11.4670 ) é certamente de uma magnitude diferente de todos os outros. Neste caso, deve haver pouca dúvida de que o ponto de dados vermelho é influente!

Distância de Cook

Apenas pulando bem aqui, a medida de distância de Cook, denominada Di, é definida como:

\.\]

Parece um pouco confuso, mas o principal a reconhecer é que a Di de Cook depende tanto do residual, ei (no primeiro termo), quanto da alavancagem, hii (no segundo termo). Ou seja, tanto o valor x como o valor y do ponto de dados desempenham um papel no cálculo da distância de Cook.

Em resumo:

• Di resume diretamente o quanto todos os valores ajustados mudam quando a observação ith é apagada.
• Um ponto de dados com um Di grande indica que o ponto de dados influencia fortemente os valores ajustados.

Vamos investigar o que exatamente essa primeira afirmação significa no contexto de alguns dos nossos exemplos.

Exemplo #1 (novamente). Você pode se lembrar que o gráfico destes dados (influência1.txt) sugere que não há outliers nem pontos de dados influentes para este exemplo:

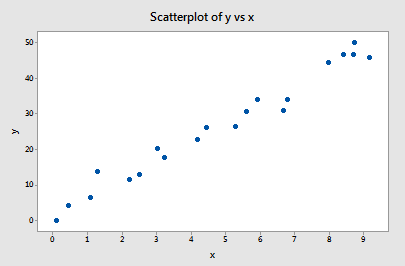
Se regredirmos y em x usando todos os n = 20 pontos de dados, determinamos que o coeficiente de intercepção estimado b0 = 1,732 e o coeficiente de inclinação estimado b1 = 5,117. Se removermos o primeiro ponto de dados do conjunto de dados, e regredirmos y sobre x usando os restantes n = 19 pontos de dados, determinamos que o coeficiente de intercepção estimado b0 = 1,732 e o coeficiente de inclinação estimado b1 = 5,1169. Como esperamos e esperamos, as estimativas não mudam muito quando removemos um ponto de dados. Continuando este processo de remoção de cada ponto de dados um de cada vez, e traçando os declives estimados resultantes (b1) versus interceptações estimadas (b0), obtemos:

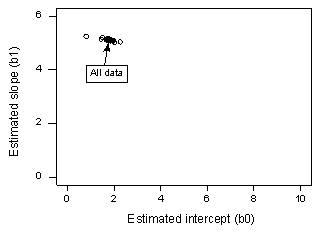
O ponto negro sólido representa os coeficientes estimados com base em todos os n = 20 pontos de dados. Os círculos abertos representam cada um dos coeficientes estimados obtidos ao eliminar cada ponto de dados, um de cada vez. Como você pode ver, os coeficientes estimados são todos agrupados, independentemente de qual, se houver, o ponto de dados é removido. Isso sugere que nenhum ponto de dados influencia indevidamente a função de regressão estimada ou, por sua vez, os valores ajustados. Neste caso, esperaríamos que todas as medidas de distância do Cook, Di, fossem pequenas.

Exemplo #4 (novamente). Você pode se lembrar que o gráfico destes dados (influência4.txt) sugere que um ponto de dados é influente e um outlier para este exemplo:

Se regredirmos y em x usando todos os n = 21 pontos de dados, determinamos que o coeficiente de intercepção estimado b0 = 8,51 e o coeficiente de inclinação estimado b1 = 3,32. Se removermos o ponto de dados vermelho do conjunto de dados, e regredirmos y sobre x usando os restantes n = 20 pontos de dados, determinamos que o coeficiente de intercepção estimado b0 = 1,732 e o coeficiente de inclinação estimado b1 = 5,1169. Uau, as estimativas mudam substancialmente com a remoção de um ponto de dados. Continuando este processo de remoção de cada ponto de dados um de cada vez, e traçando os declives estimados resultantes (b1) versus interceptações estimadas (b0), obtemos:

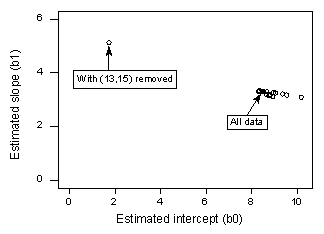
Again, o ponto preto sólido representa os coeficientes estimados com base em todos os n = 21 pontos de dados. Os círculos abertos representam cada um dos coeficientes estimados obtidos ao eliminar cada ponto de dados, um de cada vez. Como você pode ver, com exceção do ponto de dados vermelho (x = 13, y = 15), os coeficientes estimados são todos agrupados, independentemente de qual, se houver, o ponto de dados é removido. Isso sugere que o ponto de dados vermelho é o único ponto de dados que influencia indevidamente a função de regressão estimada e, por sua vez, os valores ajustados. Neste caso, seria de esperar que a medida de distância do Cook, Di, para o ponto de dados vermelho fosse grande e as medidas de distância do Cook, Di, para os restantes pontos de dados fossem pequenos.

Using Cook’s distance measures. A beleza dos exemplos acima é a capacidade de ver o que está a acontecer com os gráficos simples. Infelizmente, não podemos confiar em gráficos simples no caso de regressão múltipla. Ao invés disso, devemos confiar nas diretrizes para decidir quando a medida de distância de um Cook é grande o suficiente para justificar o tratamento de um ponto de dados como influente.

Aqui estão as diretrizes comumente usadas:

• Se Di é maior que 0,5, então o i-ésimo ponto de dados é digno de mais investigação, pois pode ser influente.
• Se Di é maior que 1, então o i-ésimo ponto de dados é bastante provável que seja influente.
• Ou, se Di se destaca como um polegar dorido dos outros valores de Di, ele é quase certamente influente.

Exemplo #2 (novamente). Vamos verificar a medida de distância do Cook para este conjunto de dados (influência2.txt):

Regressing y on x e solicitando as medidas de distância do Cook, obtemos a seguinte saída do software:

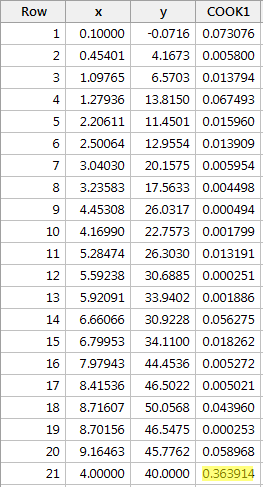
A medida de distância do Cook para o ponto de dados vermelho (0,363914) destaca-se um pouco em comparação com as outras medidas de distância do Cook. Ainda assim, a medida de distância do Cook para o ponto de dados vermelho é inferior a 0,5. Portanto, com base na medida de distância do Cook, não classificaríamos o ponto de dados vermelho como sendo influente.

Exemplo #3 (novamente). Vamos verificar a medida de distância do Cook para este conjunto de dados (influência3.txt):

Regressing y on x e solicitando as medidas de distância do Cook, obtemos a seguinte saída do software:

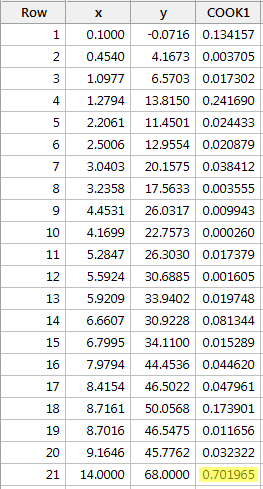
A medida de distância do Cook para o ponto de dados vermelho (0,701965) destaca-se um pouco em comparação com as outras medidas de distância do Cook. Ainda assim, a medida de distância do Cook para o ponto de dados vermelho é mais greta que 0,5 mas menos que 1. Portanto, com base na medida de distância do Cook, talvez investigássemos mais, mas não necessariamente classificássemos o ponto de dados vermelho como sendo influente.

Exemplo #4 (novamente). Vamos verificar a medida de distância do Cook para este conjunto de dados (influence4.txt):

Regressing y on x e solicitando as medidas de distância do Cook, obtemos a seguinte saída do software:

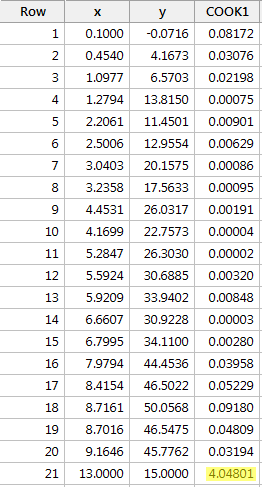
Neste caso, a medida de distância do Cook para o ponto de dados vermelho (4.04801) destaca-se substancialmente em comparação com as outras medidas de distância do Cook. Além disso, a medida de distância de Cook para o ponto de dados vermelho é maior que 1. Portanto, com base na medida de distância de Cook – e não surpreendentemente – classificaríamos o ponto de dados vermelho como sendo influente.

Um método alternativo para interpretar a distância de Cook que às vezes é usado é relacionar a medida com a distribuição F(k+1, n-k-1) e encontrar o valor do percentil correspondente. Se este percentil for inferior a cerca de 10 ou 20 por cento, então o caso tem pouca influência aparente sobre os valores ajustados. Por outro lado, se estiver próximo de 50% ou até mais, então o case tem uma influência maior. (Qualquer coisa “entre” é mais ambígua.)