Wprowadzenie spójnego haszowania

Jako szybkie wprowadzenie do haszowania ważne jest, aby zrozumieć, że główną ideą jest rozprzestrzenianie wartości w domenie. Na przykład:

• MD5 rozkłada wartości na 128-bitową domenę przestrzeni
• Hashtable (lub hashmap) wspierana przez tablicę 32 elementów ma wewnętrzną funkcję haszującą, która rozkłada wartości na dowolny indeks (od 0 do 31).

Rozkład obciążenia

Rozkład obciążenia można zdefiniować jako proces rozkładania obciążenia na węzły. Termin węzeł jest tu zamiennie używany z terminem serwer lub instancja. Jest to jednostka obliczeniowa.

Load balancing jest jednym z przykładów dystrybucji obciążenia. Polega ono na rozdzielaniu zestawu zadań na zestaw zasobów. Na przykład, używamy równoważenia obciążenia do dystrybucji żądań API pomiędzy instancjami serwera WWW.

Jeśli chodzi o dane, używamy raczej terminu sharding. Shard bazy danych jest poziomą partycją danych w bazie danych. Typowym przykładem jest baza danych podzielona na trzy shardy, gdzie każdy shard posiada podzbiór wszystkich danych.

Load balancing i sharding dzielą pewne wspólne wyzwania. Rozkładanie danych równomiernie, na przykład w celu zagwarantowania, że węzeł nie jest przeciążony w porównaniu do innych. W pewnym kontekście równoważenie obciążenia i sharding wymagają również ciągłego kojarzenia zadań lub danych z tym samym węzłem:

• Jeśli potrzebujemy serializować, obsługiwać jeden po drugim, operacje dla danego konsumenta, musimy kierować żądanie do tego samego węzła.
• Jeśli potrzebujemy dystrybuować dane, musimy wiedzieć, który shard jest właścicielem dla danego klucza.

Czy brzmi to znajomo? W tych dwóch przykładach, rozprowadzamy wartości po domenie. Czy to zadanie rozłożone na węzły serwera lub dane rozłożone na shardzie bazy danych, znajdujemy z powrotem ideę związaną z haszowaniem. To jest powód, dla którego hashowanie może być używane w połączeniu z dystrybucją obciążenia. Zobaczmy jak.

Mod-n Hashing

Zasada mod-n hashowania jest następująca. Każdy klucz jest haszowany przy użyciu funkcji haszującej, aby przekształcić dane wejściowe w liczbę całkowitą. Następnie wykonujemy modulo w oparciu o liczbę węzłów.

Zobaczmy konkretny przykład z 3 węzłami. Tutaj musimy rozdzielić obciążenie między te węzły w oparciu o identyfikator klucza. Każdy klucz jest haszowany, a następnie wykonujemy operację modulo:

Zaletą tego podejścia jest jego bezpaństwowość. Nie musimy utrzymywać żadnego stanu, który przypominałby nam, że foo został skierowany do węzła 2. Musimy jednak wiedzieć, ile węzłów jest skonfigurowanych, aby zastosować operację modulo.

Jak zatem działa ten mechanizm w przypadku skalowania w górę lub w dół (dodawania lub usuwania węzłów)? Jeśli dodamy kolejny węzeł, to operacja modulo jest teraz oparta na 4 zamiast 3:

Jak widzimy, klucze foo i baz nie są już skojarzone z tym samym węzłem. W przypadku haszowania mod-n nie ma gwarancji, że zachowana zostanie jakakolwiek spójność w skojarzeniu klucz-węzeł. Czy to jest problem? Może.

Co jeśli zaimplementujemy magazyn danych używając shardingu i bazując na strategii mod-n do dystrybucji danych? Jeśli skalujemy liczbę węzłów, musimy wykonać operację rebalansowania. W poprzednim przykładzie rebalansowanie oznacza:

• Przeniesienie foo z węzła 2 do węzła 0.
• Przeniesienie baz z węzła 2 do węzła 3.

A teraz, co by się stało, gdybyśmy przechowywali miliony lub nawet miliardy danych i musieli zrebalansować prawie wszystko? Jak możemy sobie wyobrazić, byłby to ciężki proces. Dlatego musimy zmienić naszą technikę dystrybucji obciążenia, aby upewnić się, że podczas rebalansowania:

• Rozkład pozostanie tak jednolity, jak to tylko możliwe w oparciu o nową liczbę węzłów.
• Liczba kluczy, które musimy zmigrować powinna być ograniczona. Idealnie byłoby, gdyby było to tylko 1/n procent kluczy, gdzie n jest liczbą węzłów.

To jest dokładnie cel spójnych algorytmów haszujących.

Termin spójny może być jednak nieco mylący. Spotkałem się z inżynierami, którzy zakładali, że takie algorytmy przypisują dany klucz do tego samego węzła nawet w obliczu skalowalności. Tak nie jest. Musi on być spójny do pewnego momentu, aby dystrybucja była jednolita.

Teraz czas zagłębić się w pewne rozwiązania.

Rendezvous

Rendezvous był pierwszym algorytmem zaproponowanym do rozwiązania naszego problemu. Chociaż oryginalne opracowanie, opublikowane w 1996 roku, nie wspomina o terminie konsekwentnego haszowania, dostarcza ono rozwiązania dla opisanych przez nas wyzwań. Zobaczmy jedną z możliwych implementacji w Go:

Jak to działa? Przechodzimy przez każdy węzeł i obliczamy jego wartość hash. Wartość haszowania jest zwracana przez funkcję hash, która tworzy liczbę całkowitą na podstawie klucza (nasze dane wejściowe) i identyfikatora węzła (najprostszym podejściem jest haszowanie konkatenacji tych dwóch łańcuchów). Następnie zwracamy węzeł o największej wartości hashowania. Jest to powód, dla którego algorytm ten jest również znany jako haszowanie o największej losowej wadze.

Główną wadą rendezvous jest jego złożoność czasowa O(n), gdzie n jest liczbą węzłów. Jest to bardzo wydajne, jeśli musimy mieć ograniczoną liczbę węzłów. Jednak jeśli zaczniemy utrzymywać tysiące węzłów, może zacząć powodować problemy z wydajnością.

Ring Consistent Hash

Kolejny algorytm został wydany w 1997 roku przez Karger et al. w tym artykule. W pracy tej po raz pierwszy pojawił się termin konsekwentnego hashowania.

Opiera się on na pierścieniu (tablicy połączonej koniec do końca). Chociaż jest to najpopularniejszy spójny algorytm haszujący (lub przynajmniej najbardziej znany), zasada działania nie zawsze jest dobrze rozumiana. Zanurzmy się w nim.

Pierwszą operacją jest utworzenie pierścienia. Pierścień ma stałą długość. W naszym przykładzie dzielimy go na 12 części:

Następnie pozycjonujemy nasze węzły. W naszym przykładzie zdefiniujemy N0, N1 i N2.

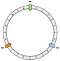
Węzły są na razie rozmieszczone równomiernie. Wrócimy do tego punktu później.

Potem czas zastanowić się, jak reprezentować klucze. Po pierwsze, potrzebujemy funkcji f, która zwraca indeks pierścienia (od 0 do 11) na podstawie klucza. Możemy do tego użyć haszowania mod-n. Ponieważ długość pierścienia jest stała, nie sprawi nam to żadnego problemu.

W naszym przykładzie zdefiniujemy 3 klucze: a, b i c. Na każdym z nich zastosujemy f. Załóżmy, że mamy następujące wyniki:

• f(a) = 1
• f(a) = 5
• f(a) = 7

W związku z tym możemy rozmieścić klucze na pierścieniu w ten sposób:

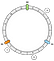
Jak skojarzyć dany klucz z węzłem? Główną logiką jest poruszanie się do przodu. Z danego klucza zwracamy pierwszy węzeł, który znajdziemy jako następny podczas posuwania się do przodu:

W tym przykładzie kojarzymy a z N1, b i c z N2.

Zobaczmy teraz, jak zarządzane jest równoważenie. Definiujemy kolejny węzeł N3. Gdzie powinniśmy go umieścić? Nie ma już miejsca na to, aby ogólna dystrybucja była jednolita. Czy powinniśmy zreorganizować węzły? Nie, w przeciwnym razie nie bylibyśmy już spójni, prawda? Aby pozycjonować węzeł, używamy ponownie tej samej funkcji haszującej f, którą wprowadziliśmy. Zamiast wywoływać ją za pomocą klucza, można ją wywołać za pomocą identyfikatora węzła. Tak więc pozycja nowego węzła jest ustalana losowo.

Rodzi się wtedy jedno pytanie: co zrobić z a, skoro kolejnym węzłem nie jest już N1:

Rozwiązanie jest następujące: musimy zmienić jego asocjację i sprawić, by a był skojarzony z N3:

Jak omawialiśmy wcześniej, idealny algorytm powinien rebalansować średnio 1/n procent kluczy. W naszym przykładzie, ponieważ dodajemy czwarty węzeł, powinniśmy mieć 25% możliwych kluczy reasocjowanych do N3. Czy tak jest?

• N0 z indeksów od 8 do 12: 33.3% całkowitych kluczy
• N1 z indeksów od 2 do 4: 16.6% całkowitych kluczy
• N2 z indeksów od 4 do 8: 33.3% wszystkich kluczy
• N3 z indeksów od 0 do 2: 16,6% wszystkich kluczy

Rozkład nie jest równomierny. Jak możemy to poprawić? Rozwiązaniem jest użycie wirtualnych węzłów.

Powiedzmy, że zamiast pozycjonować jeden punkt na węzeł, możemy pozycjonować trzy. Ponadto, musimy zdefiniować trzy różne funkcje haszujące. Każdy węzeł jest haszowany trzykrotnie, dzięki czemu otrzymujemy trzy różne indeksy:

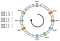
Możemy zastosować ten sam algorytm, przesuwając się do przodu. W tym przykładzie rozkład byłby następujący:

• N0: 33.3%
• N1: 25%
• N2: 41.6%

Im więcej węzłów wirtualnych zdefiniujemy na węzeł, tym bardziej rozkład powinien być równomierny. Średnio, przy 100 wirtualnych węzłach na serwer, standardowa dystrybucja wynosi około 10%. Przy 1000 jest to około 3,2%.

Mechanizm ten jest również przydatny, gdy mamy węzły o różnej wielkości. Na przykład, jeśli węzeł jest skonfigurowany do teoretycznie dwukrotnie większego obciążenia niż pozostałe, możemy uruchomić dwa razy więcej węzłów wirtualnych.

Jednakże, głównym minusem węzłów wirtualnych jest ślad pamięciowy. Gdybyśmy musieli obsłużyć tysiące serwerów, wymagałoby to megabajtów pamięci.

Zanim przejdziemy dalej, warto zauważyć, że czasami algorytm można znacznie ulepszyć, zmieniając niewielką jego część. Tak jest na przykład w przypadku algorytmu opublikowanego przez Google w 2017 roku o nazwie consistent hashing with bounded loads. Ta wersja opiera się na tej samej idei pierścienia, którą opisaliśmy. Jednak ich podejście polega na wykonaniu małego rebalansu przy każdej aktualizacji (nowy klucz lub węzeł dodany/usunięty). Ta wersja przewyższa oryginalną pod względem odchylenia standardowego z kompromisem w postaci najgorszej złożoności czasowej.

Jump Consistent Hash

W 2007 roku, dwóch inżynierów z Google opublikowało jump consistent hash. W porównaniu do algorytmu opartego na pierścieniu, ta implementacja „nie wymaga przechowywania, jest szybsza i wykonuje lepszą pracę równomiernie dzieląc przestrzeń klucza między wiadra i równomiernie dzieląc obciążenie, gdy zmienia się liczba wiader”. Innymi słowy, poprawia dystrybucję obciążenia pomiędzy węzłami (kubełek jest tym samym pojęciem co węzeł) bez żadnego narzutu pamięci.

Tutaj algorytm w C++ (7 linii kodu 🤯):

W ring consistent hash, z 1000 wirtualnych węzłów odchylenie standardowe wynosiło około 3,2%. W jump consistent hash, nie potrzebujemy już koncepcji wirtualnych węzłów. Mimo to, odchylenie standardowe pozostaje mniejsze niż 0.0000001%.

Jest jednak jedno ograniczenie. Węzły muszą być ponumerowane kolejno. Jeśli mamy listę serwerów foo, bar i baz, nie możemy na przykład usunąć bar. Jednak, jeśli skonfigurujemy magazyn danych, możemy zastosować algorytm, aby uzyskać indeks shardów w oparciu o całkowitą liczbę shardów. Dlatego też, jump consistent hash może być użyteczny w kontekście shardingu, ale nie load balancing.

Co to jest Perfect Consistent Hashing Algorithm?

Jako że mamy już pewne doświadczenie z konsekwentnym hashowaniem, zróbmy krok wstecz i zobaczmy, jaki byłby idealny algorytm:

• Średnio tylko 1/n procent kluczy zostałoby przemapowanych, gdzie n jest liczbą węzłów.
• Złożoność przestrzeni O(n), gdzie n jest liczbą węzłów.
• A O(1) złożoność czasowa na wstawienie/usunięcie węzła i na odszukanie klucza.
• A minimalne odchylenie standardowe, aby upewnić się, że węzeł nie jest przeciążony w porównaniu z innym.
• To pozwoliłoby na przypisanie wagi do węzła, aby poradzić sobie z różnymi rozmiarami węzłów.
• To pozwoliłoby na dowolne nazwy węzłów (nie numerowane sekwencyjnie), aby wspierać zarówno równoważenie obciążenia, jak i sharding.

Niestety, ten algorytm nie istnieje. Na podstawie tego, co widzieliśmy:

• Rendezvous ma liniową złożoność czasową na lookup.
• Ring consistent hash ma słabe minimalne odchylenie standardowe bez koncepcji wirtualnych węzłów. Z wirtualnymi węzłami, złożoność przestrzeni jest O(n*v) z n liczbą węzłów i v liczbą wirtualnych węzłów na węzeł.
• Jump spójny hash nie ma stałej złożoności czasowej i nie obsługuje arbitralne nazwy węzłów.

Temat jest nadal otwarty i istnieją ostatnie badania, które są warte spojrzenia. Na przykład, wielopróbkowy spójny hash wydany w 2005 roku. Obsługuje on złożoność przestrzeni O(1). Jednak, aby osiągnąć odchylenie standardowe ε, wymaga O(1/ε) czasu na lookup. Na przykład, jeśli chcemy osiągnąć odchylenie standardowe mniejsze niż 0,5%, wymaga to haszowania klucza około 20 razy. Dlatego możemy uzyskać minimalne odchylenie standardowe, ale w wysiłku wyższej złożoności czasowej lookup.

Jak powiedzieliśmy we wstępie, spójne algorytmy haszujące stały się głównym nurtem. Jest on obecnie używany w niezliczonych systemach takich jak MongoDB, Cassandra, Riak, Akka, itp. czy to w kontekście równoważenia obciążenia czy dystrybucji danych. Jednak, jak to często bywa w informatyce, każde rozwiązanie ma swoje kompromisy.

Mówiąc o kompromisach, jeśli potrzebujesz kontynuacji, możesz rzucić okiem na świetny post napisany przez Damiana Gryskiego: