Test Friedmana w SPSS Statistics

SPSS Statistics

Wyjście dla testu Friedmana

SPSS Statistics wygeneruje dwie lub trzy tabele, w zależności od tego, czy wybrałeś generowanie statystyk opisowych i/lub kwartyli oprócz uruchomienia testu Friedmana.

Tabela Statystyki opisowe

Tabela Statystyki opisowe zostanie wygenerowana, jeśli wybrano opcję Kwartyle:

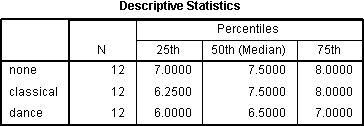
Published with written permission from SPSS Statistics, IBM Corporation.

Jest to bardzo użyteczna tabela, ponieważ może być użyta do przedstawienia statystyk opisowych w sekcji wyników dla każdego z punktów czasowych lub warunków (w zależności od projektu badania) dla zmiennej zależnej. Ta użyteczność zostanie przedstawiona w sekcji „Raportowanie danych wyjściowych” w dalszej części rozdziału.

Tabela rang

Tabela rang pokazuje średnią rangę dla każdej z powiązanych grup, jak pokazano poniżej:

Published with written permission from SPSS Statistics, IBM Corporation.

Test Friedmana porównuje średnie rangi między powiązanymi grupami i wskazuje, w jaki sposób grupy się różniły, i z tego powodu jest uwzględniony. Jednak jest mało prawdopodobne, abyś faktycznie zgłosił te wartości w swojej sekcji wyników, ale najprawdopodobniej zgłosisz wartość mediany dla każdej powiązanej grupy.

Tabela statystyk testu

Tabela statystyk testu informuje o faktycznym wyniku testu Friedmana i o tym, czy istniała ogólna statystycznie istotna różnica między średnimi rangami powiązanych grup. Dla przykładu użytego w tym przewodniku, tabela wygląda następująco:

Published with written permission from SPSS Statistics, IBM Corporation.

Powyższa tabela podaje wartość statystyki testowej (χ2) („Chi-square”), stopnie swobody („df”) i poziom istotności („Asymp. Sig.”), czyli wszystko, czego potrzebujemy, aby podać wynik testu Friedmana. Z naszego przykładu widać, że istnieje ogólna statystycznie istotna różnica między średnimi rangami powiązanych grup. Ważne jest, aby zauważyć, że test Friedmana jest testem zbiorczym, podobnie jak jego parametryczna alternatywa; to znaczy, że mówi on, czy istnieją ogólne różnice, ale nie wskazuje, które grupy w szczególności różnią się od siebie. Aby to zrobić, musisz przeprowadzić testy post hoc, które zostaną omówione w następnej sekcji.

SPSS Statistics

Reporting the Output of the Friedman Test (without post hoc tests)

Możesz przedstawić wynik testu Friedmana w następujący sposób:

Mógłbyś również dołączyć mediany wartości dla każdej z powiązanych grup. Jednak na tym etapie wiesz tylko, że istnieją różnice gdzieś pomiędzy powiązanymi grupami, ale nie wiesz dokładnie, gdzie te różnice leżą. Pamiętaj jednak, że jeśli wynik testu Friedmana nie był statystycznie istotny, nie powinieneś przeprowadzać testów post hoc.

Testy post hoc

Aby zbadać, gdzie faktycznie występują różnice, musisz przeprowadzić oddzielne testy Wilcoxon signed-rank na różnych kombinacjach powiązanych grup. Tak więc, w tym przykładzie, porównałbyś następujące kombinacje:

• Brak do Klasyki.
• Brak do Tańca.
• Klasyczna do Tańca.

Musisz użyć korekty Bonferroniego na wynikach, które otrzymujesz z testów Wilcoxona, ponieważ dokonujesz wielokrotnych porównań, co zwiększa prawdopodobieństwo, że uznasz wynik za znaczący, gdy nie powinieneś (błąd typu I). Na szczęście, korekta Bonferroniego jest bardzo łatwa do obliczenia; po prostu weź poziom istotności, którego początkowo używałeś (w tym przypadku 0,05) i podziel go przez liczbę testów, które przeprowadzasz. Tak więc w tym przykładzie mamy nowy poziom istotności 0,05/3 = 0,017. Oznacza to, że jeśli wartość p jest większa niż 0,017, nie mamy statystycznie istotnego wyniku.

Przeprowadzając te testy (zobacz jak z naszym przewodnikiem po teście Wilcoxon signed-rank) na wynikach z tego przykładu, otrzymujemy następujący wynik:

Published with written permission from SPSS Statistics, IBM Corporation.

Ta tabela pokazuje wynik testu Wilcoxon signed-rank dla każdej z naszych kombinacji. Należy zauważyć, że wartości istotności nie zostały skorygowane w SPSS Statistics, aby skompensować wielokrotne porównania – musisz ręcznie porównać wartości istotności uzyskane przez SPSS Statistics z poziomem istotności skorygowanym przez Bonferroniego, który sam obliczyłeś. Widzimy, że na poziomie istotności p < 0.017, tylko postrzegany wysiłek pomiędzy brakiem muzyki a tańcem (dance-none, p = 0.008) był statystycznie istotnie różny.

SPSS Statistics

Reporting the Output of the Friedman Test (with post hoc tests)

Możesz raportować wyniki testu Friedmana z testami post hoc w następujący sposób: