Rezonans Helmholtza
- Analiza rezonansu Helmholtza
- Rezonans, impedancja, zależność fazowa i częstotliwościowa
- Komplikacje związane z długością
- Rezonanse Helmholtza a gitary
Analiza rezonansu Helmholtza
Teraz zajmijmy się kwestią ilościową: Przede wszystkim założymy, że długość fali wytwarzanego dźwięku jest znacznie większa od wymiarów rezonatora. Dla butelek z animacji na górze tej strony długości fali wynoszą odpowiednio 180 i 74 cm, więc to przybliżenie jest całkiem niezłe, ale warto je sprawdzić za każdym razem, gdy zaczynamy opisywać coś jako oscylator Helmholtza. Konsekwencją tego przybliżenia jest to, że możemy zaniedbać zmiany ciśnienia wewnątrz objętości pojemnika: oscylacje ciśnienia będą miały tę samą fazę wszędzie wewnątrz pojemnika.
Niech powietrze w szyjce ma długość efektywną L i pole przekroju poprzecznego S. Jego masa jest wtedy SL razy gęstość powietrza ρ. (Pewne komplikacje dotyczące długości efektywnej są omówione na końcu tej strony). Jeśli ten „korek” powietrza zejdzie na niewielką odległość x do butelki, to spręża on powietrze w pojemniku tak, że powietrze, które wcześniej zajmowało objętość V, teraz ma objętość V – Sx. W konsekwencji ciśnienie tego powietrza wzrasta z ciśnienia atmosferycznego PA do wyższej wartości PA + p.
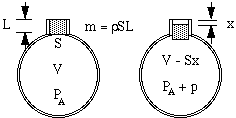
Teraz można by pomyśleć, że wzrost ciśnienia będzie po prostu proporcjonalny do spadku objętości. Tak by było, gdyby ściskanie odbywało się tak wolno, że temperatura nie uległaby zmianie. W wibracjach, które powodują powstawanie dźwięku, zmiany są jednak szybkie i dlatego temperatura wzrasta przy ściskaniu, co daje większą zmianę ciśnienia. Z technicznego punktu widzenia są one adiabatyczne, co oznacza, że ciepło nie ma czasu się przemieszczać, a wynikające z tego równanie zawiera stałą γ, stosunek ciepła właściwego, który wynosi około 1,4 dla powietrza. (Jest to wyjaśnione w dodatku.) W rezultacie, zmiana ciśnienia p wytworzona przez małą zmianę objętości ΔV jest tylko
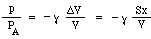
Teraz masa m jest przemieszczana przez różnicę ciśnienia między górną i dolną częścią szyi, tj. siłę netto pS, więc piszemy prawo Newtona dla przyspieszenia a:
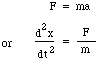
podstawiając za F i m daje: 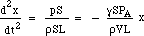
Zatem siła przywracająca jest proporcjonalna do przemieszczenia. Jest to warunek ruchu harmonicznego prostego, a ma on częstotliwość, która jest 1/2π razy pierwiastek kwadratowy ze stałej proporcjonalności, więc
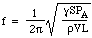
Teraz prędkość c dźwięku w powietrzu zależy od gęstości, ciśnienia i stosunku ciepła właściwego, więc możemy napisać:
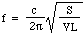
Wstawmy kilka liczb: dla butelki o pojemności 1 litra, o S = 3 centymetry kwadratowe i L = 5 centymetrów, częstotliwość wynosi 130 Hz, czyli około C poniżej środkowego C. (Patrz uwagi.) Zatem długość fali wynosi 2,6 metra, czyli jest znacznie większa niż butelka. To uzasadnia, post hoc, założenie przyjęte na początku wyprowadzenia.
Resonans, impedancja, zależność fazowa i częstotliwościowa
Ten rozdział można czytać samodzielnie, ale jeśli chcesz uzyskać bardziej szczegółowe tło, zobacz Oscylacje, Oscylacje wymuszone i Zgodność akustyczna, obojętność i impedancja.
Powróćmy do mechanicznej reprezentacji i spójrzmy na rezonator Helmholtza z zewnątrz, jak pokazano na pierwszym schemacie: popychamy siłą oscylacyjną F, z częstotliwością f , masę m (powietrze w szyjce rezonatora), która jest podparta na sprężynie (zamknięte powietrze) o stałej sprężystości k, której drugi koniec jest nieruchomy (powietrze w rezonatorze nie może uciec). Nierealistycznie, zaniedbamy grawitację i tarcie (na razie).
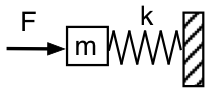
Siła potrzebna do przyspieszenia masy jest proporcjonalna do przyspieszenia, a więc proporcjonalna do f2. Przy dostatecznie małej częstotliwości siła potrzebna do przyspieszenia masy jest pomijalna, więc F musi tylko ściskać i rozciągać sprężynę. Zatem w tej granicy przyłożona siła F = +kx. (Siła sprężyny wynosi -kx.) Impedancja mechaniczna układu przy tak niskiej częstotliwości jest zgodna lub podobna do sprężyny. Akustycznie, wygląda to jak zgodność akustyczna: popychamy masę powietrza w szyjce i ściskamy powietrze w rezonatorze. Przyłożona siła F po prawej stronie jest w fazie z x mierzonym po prawej stronie, więc jest 90° za prędkością, a przyłożone ciśnienie jest 90° za przepływem akustycznym do rezonatora.
Pamiętajmy, że f2 zależy od przyspieszenia. Tak więc, przy dostatecznie dużej częstotliwości, siła sprężyny jest pomijalna w porównaniu z siłą przyspieszającą masę. Zatem F jest w fazie z przyspieszeniem, co stawia ją 90° przed prędkością. Akustycznie, przyłożony nacisk jest 90° przed przepływem akustycznym do rezonatora. Jest to bezwładność mechaniczna lub akustyczna.
Przy częstotliwości rezonansowej (nadal mówimy o szkicu powyżej), amplituda może być duża dla bardzo małej siły. Zatem w rezonansie impedancja jest bardzo mała, patrząc z perspektywy siły przyłożonej do masy z zewnątrz (schemat powyżej). W rezonansie występuje maksymalny przepływ do i z rezonatora.
Rozważmy teraz, co się stanie, jeśli spojrzymy na ciśnienie wewnątrz rezonatora (z dala od szyjki). Tutaj patrzymy na siłę działającą na sprężynę, więc nasz mechaniczny analog wygląda jak na tym schemacie.
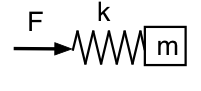
Tym razem niska częstotliwość oznacza, że siła może być mała dla danej amplitudy: sprężyna i masa poruszają się razem jako masa, a układ tym razem wygląda na bezwładny przy niskiej częstotliwości. Przy wysokiej częstotliwości masa prawie się nie porusza, a układ jest sprężysty lub podatny. Zależności fazowe są więc odwrotne niż poprzednio: przy niskich f, p przewodzi U o 90°; przy wysokich f, p pozostaje w tyle za U o 90°.
Komplikacje związane z długością efektywną
Pierwszy diagram na tej stronie rysuje „korek” powietrza tak, jakby był on cylindrem, który kończy się dokładnie na obu końcach szyjki butelki. Jest to zbytnie uproszczenie. W praktyce, dodatkowa objętość zarówno wewnątrz jak i na zewnątrz porusza się wraz z powietrzem w szyjce – jak sugeruje powyższa animacja. Dodatkowa długość, która powinna być dodana do geometrycznej długości szyjki jest zwykle (i bardzo w przybliżeniu) 0,6 promienia na zewnętrznym końcu, i jeden promień na wewnętrznym końcu).
|
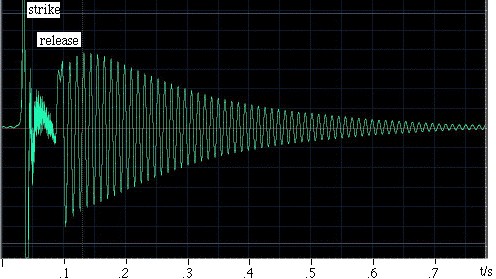
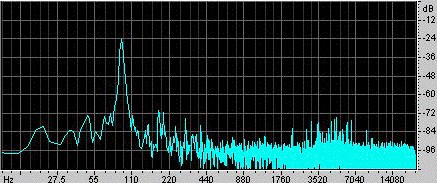
Przykład. Ra Inta stworzył ten przykład. Wziął on sferyczny rezonator Helmholtza o objętości 0,00292 m3 i cylindrycznej szyjce o długości 0,080 m i powierzchni przekroju 0,00083 m2. Aby go wzbudzić, uderzył w niego dłonią, a następnie puścił. Mikrofon znajdujący się wewnątrz rezonatora zarejestrował dźwięk, który został przedstawiony na oscylogramie po lewej stronie. Widać, że dłoń uszczelnia rezonator na krócej niż 0.1 s, a w tym czasie oscylacje są słabsze i mają stosunkowo wysoką częstotliwość. Od momentu zwolnienia ręki powstają oscylacje, które stopniowo wygasają, ponieważ tracą energię przez opór lepki i turbulentny, a także przez promieniowanie dźwiękowe. Dokładna analiza wykazuje, że częstotliwość nieznacznie wzrasta w miarę oddalania się ręki od otwartego końca, ponieważ ręka ogranicza kąt bryłowy dostępny dla promieniowania i w ten sposób zwiększa efekt końcowy (lub korekcję końcową). Długość szyjki zwiększa się o jeden przegrodzony i jeden nie przegrodzony efekt końcowy, co daje jej efektywną długość 0,105 m. Przy prędkości dźwięku 343 m/s, powyższe wyrażenie daje częstotliwość rezonansową 90 Hz. |
|
Rezonanse Helmholtza i gitary
* Powiedziałem powyżej, że powietrze w korpusie gitary zachowuje się prawie jak oscylator Helmholtza. Sprawa jest skomplikowana, ponieważ korpus może nieco puchnąć, gdy ciśnienie powietrza w nim wzrasta – a także dlatego, że powietrze „w” otworze dźwiękowym gitary ma geometrię, która jest mniej łatwa do zobrazowania niż ta w szyjce butelki. Rzeczywiście, w przypadku korpusu gitary długość korka powietrza jest w przybliżeniu równa dwóm „efektom końcowym” na końcu „rury”, która ma tylko kilka mm grubości. Efekty końcowe są jednak związane i mają wielkość zbliżoną do promienia otworu, a więc masa powietrza jest znaczna. Długość efektu końcowego cylindrycznej rury, która otwiera się na nieskończoną, płaską przegrodę, jest 0,85 promienia rury. Chociaż płyta rezonansowa gitary nie jest nieskończona, można by się spodziewać podobnego efektu końcowego, a więc efektywna długość „korka” powietrza byłaby około 1,7 razy większa od promienia otworu. (Niektórzy producenci zwiększają tę wartość poprzez zamocowanie krótkiej rurki poniżej otworu dźwiękowego, o takim samym promieniu).
Kilka osób pisało z pytaniem, jak duży powinien być otwór dla danego instrumentu. Cóż, możemy użyć powyższego równania, aby zacząć odpowiadać na to pytanie. Ważne jest jednak spęcznienie korpusu. Sprawia to, że „sprężyna” powietrza jest bardziej miękka, a więc obniża częstotliwość. Czysty rezonans Helmholtza może być zbadany poprzez utrzymanie stałej objętości ciała. Częstą praktyką podczas pomiarów jest zakopanie gitary w piasku, aby utrudnić pęcznienie lub „oddychanie” korpusu. Gitary nie są jednak zwykle grane w takiej sytuacji. Tak więc obliczenia Helmholtza dadzą zawyżoną częstotliwość rezonansową dla prawdziwego, elastycznego korpusu.
Załóżmy okrągły otwór dźwiękowy o promieniu r, więc S = πr2, i L = 1.7r, jak wyjaśniono powyżej. Gdy podstawimy do równania na częstotliwość Helmholtza, używając c = 340 m/s, otrzymamy:
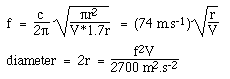
Zauważmy, że używamy standardowych jednostek SI: użyliśmy prędkości dźwięku w metrach i sekundach, więc objętość musi być w metrach sześciennych, a częstotliwość w hercach, aby dać odpowiedź w metrach.
Jest to bardziej skomplikowane, gdy otwory tonowe nie są okrągłe, ponieważ efekt końcowy nie jest równy temu, jaki daje okrąg o tej samej powierzchni. Doktorant i lutnik John McLennan pisze raport z pomiarów na ten temat, który wkrótce tu zamieścimy.
Na instrumentach z rodziny gitar i skrzypiec, rezonans Helmholtza (plus korpus) jest często blisko lub trochę poniżej częstotliwości drugiej najniższej struny, około D na skrzypcach lub G-A na gitarze. Możesz znacznie zmniejszyć lub przesunąć częstotliwość Helmholtza zakrywając całość lub część otworu odpowiednio ukształtowanym kawałkiem sztywnej tektury. Jeśli zagrasz wtedy nutę w pobliżu rezonansu, a następnie przesuniesz kartkę tak, aby na przemian zakrywała i odsłaniała otwór, to wyraźnie usłyszysz efekt rezonansu.
Czy efekt 0,85r jest uzasadniony? Ra Inta, który zrobił doktorat z akustyki gitary w naszym laboratorium, proponuje ciekawą demonstrację:
Zawilż struny w gitarze, aby nie drgały (np. chusteczką między strunami a podstrunnicą). Trzymaj dłoń jednej ręki nad otworem akustycznym, blisko niego. Palcem drugiej ręki uderzaj ostro w podstrunnicę w pobliżu otworu dźwiękowego i blisko pierwszej struny. Poczujesz pulsowanie powietrza na dłoni. Uderzenie palcem wpycha płytę rezonansową do środka i wyciska trochę powietrza z korpusu. Teraz stopniowo odsuwaj dłoń od otworu i kontynuuj stukanie palcem. Kiedy przestaniesz wyczuwać ruch powietrza? To da ci przybliżony szacunek długości „efektu końcowego” w przypadku otworu dźwiękowego.
Strojenie rezonansu Helmholtza
Wśród publikacji Johna McLennana, doktoranta z tego laboratorium, jest artykuł, w którym zmienia on rezonans Helmholtza poprzez zmianę prędkości dźwięku.
- McLennan, J.E. (2003) „A0 i A1 studies on the violin using CO2, He, and air/helium mixtures.” Acustica, 89, 176-180.
Kilka zdjęć historycznych rezonatorów Helmholtza dostarczonych przez Thomasa B. Greenslade’a, Kenyon College, Ohio.
Leave a Reply