Proces Grama-Schmidta
by Marco Taboga, PhD
Proces (lub procedura) Grama-Schmidta jest sekwencją operacji, które pozwalają na przekształcenie zbioru wektorów liniowo niezależnych w zbiór wektorów ortonormalnych, które obejmują tę samą przestrzeń, w której znajduje się zbiór oryginalny.

Preliminaria
Dokonajmy przeglądu kilku pojęć, które są niezbędne do zrozumienia procesu Grama-Schmidta.
Przypomnijmy, że o dwóch wektorach  i
i  mówi się, że są ortogonalne wtedy i tylko wtedy, gdy ich iloczyn wewnętrzny jest równy zeru, czyli,
mówi się, że są ortogonalne wtedy i tylko wtedy, gdy ich iloczyn wewnętrzny jest równy zeru, czyli,
Biorąc pod uwagę iloczyn wewnętrzny, możemy zdefiniować normę (długość) wektora  w następujący sposób:
w następujący sposób:
Zbiór wektorów nazywamy ortonormalnym wtedy i tylko wtedy, gdy jego elementy mają normę jednostkową i są względem siebie ortogonalne. Innymi słowy, zbiór  wektorów
wektorów  jest ortonormalny wtedy i tylko wtedy, gdy
jest ortonormalny wtedy i tylko wtedy, gdy
Udowodniliśmy, że wektory zbioru ortonormalnego są liniowo niezależne.
Gdy podstawa przestrzeni wektorowej jest jednocześnie zbiorem ortonormalnym, to nazywamy ją podstawą ortonormalną.
Projekcje na zbiorach ortonormalnych
W procesie Grama-Schmidta wielokrotnie korzystamy z następnej propozycji, z której wynika, że każdy wektor można rozłożyć na dwie części: 1) jego projekcję na zbiór ortonormalny oraz 2) resztę, która jest ortogonalna do danego zbioru ortonormalnego.
Propozycja Niech  będzie przestrzenią wektorową wyposażoną w iloczyn wewnętrzny
będzie przestrzenią wektorową wyposażoną w iloczyn wewnętrzny  . Niech
. Niech  będzie zbiorem ortonormalnym. Dla dowolnego
będzie zbiorem ortonormalnym. Dla dowolnego  , mamy
, mamy gdzie
gdzie  jest ortogonalny do
jest ortogonalny do  dla dowolnego
dla dowolnego 
Define Then, for each
Then, for each  , we have that
, we have that where: w krokach
where: w krokach  i
i  wykorzystaliśmy fakt, że iloczyn wewnętrzny jest liniowy w swoim pierwszym argumencie; w kroku
wykorzystaliśmy fakt, że iloczyn wewnętrzny jest liniowy w swoim pierwszym argumencie; w kroku  wykorzystaliśmy fakt, że
wykorzystaliśmy fakt, że  jeśli
jeśli  , ponieważ mamy do czynienia ze zbiorem ortonormalnym; w kroku
, ponieważ mamy do czynienia ze zbiorem ortonormalnym; w kroku  wykorzystaliśmy fakt, że norma
wykorzystaliśmy fakt, że norma  jest równa 1. Zatem
jest równa 1. Zatem  , zgodnie z powyższą definicją, jest ortogonalny do wszystkich elementów zbioru ortonormalnego, co dowodzi prawdziwości tezy.
, zgodnie z powyższą definicją, jest ortogonalny do wszystkich elementów zbioru ortonormalnego, co dowodzi prawdziwości tezy.
Wyraz nazywamy rzutem liniowym
nazywamy rzutem liniowym  na zbiór ortonormalny
na zbiór ortonormalny  , zaś wyraz
, zaś wyraz  nazywamy residuami rzutu liniowego.
nazywamy residuami rzutu liniowego.
Normalizacja
Innym, być może oczywistym faktem, który będziemy wielokrotnie wykorzystywać w procesie Grama-Schmidta jest to, że jeśli weźmiemy dowolny niezerowy wektor i podzielimy go przez jego normę, to wynikiem podziału jest nowy wektor, który ma normę jednostkową.
Innymi słowy, jeśli  to, na mocy własności definitywności normy, mamy, że
to, na mocy własności definitywności normy, mamy, że 
W konsekwencji możemy zdefiniować i, na mocy pozytywności i absolutnej jednorodności normy, mamy
i, na mocy pozytywności i absolutnej jednorodności normy, mamy
Przegląd procedury
Teraz, gdy wiemy jak znormalizować wektor i jak rozłożyć go na rzut na zbiór ortonormalny i resztę, jesteśmy gotowi do wyjaśnienia procedury Grama-Schmidta.
Zamierzamy przedstawić ogólny zarys procesu, po czym wyrazimy go formalnie jako tezę, a wszystkie szczegóły techniczne omówimy w dowodzie tej tezy.
Oto zarys.
Dany jest zbiór liniowo niezależnych wektorów  .
.
Aby rozpocząć proces, normalizujemy pierwszy wektor, czyli definiujemy
W drugim kroku rzutujemy  na
na  :
: gdzie
gdzie  jest resztą z rzutowania.
jest resztą z rzutowania.
Następnie normalizujemy resztę:
Później udowodnimy, że  (aby można było przeprowadzić normalizację), ponieważ wektory początkowe są liniowo niezależne.
(aby można było przeprowadzić normalizację), ponieważ wektory początkowe są liniowo niezależne.
Otrzymane w ten sposób dwa wektory  i
i  są ortonormalne.
są ortonormalne.
W trzecim kroku rzutujemy  na
na  i
i  :
: i obliczamy resztę projekcji
i obliczamy resztę projekcji  .
.
Następnie normalizujemy ją:
Postępujemy w ten sposób, aż otrzymamy ostatnią znormalizowaną resztę  .
.
Na końcu procesu wektory  tworzą zbiór ortonormalny, ponieważ:
tworzą zbiór ortonormalny, ponieważ:
-
są one wynikiem normalizacji, a w konsekwencji mają normę jednostkową;
-
każda
 jest otrzymana z reszt, które mają własność bycia ortogonalnymi do
jest otrzymana z reszt, które mają własność bycia ortogonalnymi do  .
.
Aby uzupełnić ten przegląd, pamiętajmy, że rozpiętość liniowa  to zbiór wszystkich wektorów, które można zapisać jako kombinacje liniowe
to zbiór wszystkich wektorów, które można zapisać jako kombinacje liniowe  ; oznaczamy ją przez
; oznaczamy ją przez i jest to przestrzeń liniowa.
i jest to przestrzeń liniowa.
Ponieważ wektory  są liniowo niezależnymi kombinacjami
są liniowo niezależnymi kombinacjami  , każdy wektor, który można zapisać jako kombinację liniową
, każdy wektor, który można zapisać jako kombinację liniową  , można również zapisać jako kombinację liniową
, można również zapisać jako kombinację liniową  . Zatem rozpiętości tych dwóch zbiorów wektorów pokrywają się:
. Zatem rozpiętości tych dwóch zbiorów wektorów pokrywają się:
Stwierdzenie formalne
Sformalizujemy tu proces Grama-Schmidta w postaci propozycji, której dowód zawiera wszystkie szczegóły techniczne procedury.
Propozycja Niech  będzie przestrzenią wektorową wyposażoną w iloczyn wewnętrzny
będzie przestrzenią wektorową wyposażoną w iloczyn wewnętrzny  . Niech
. Niech  będą wektorami liniowo niezależnymi. Wówczas istnieje zbiór wektorów ortonormalnych
będą wektorami liniowo niezależnymi. Wówczas istnieje zbiór wektorów ortonormalnych  takich, że
takich, że dla dowolnego
dla dowolnego  .
.
Dowód jest przez indukcję: najpierw dowodzimy, że teza jest prawdziwa dla  , a następnie dowodzimy, że jest prawdziwa dla ogólnego
, a następnie dowodzimy, że jest prawdziwa dla ogólnego  , jeśli zachodzi dla
, jeśli zachodzi dla  . Gdy
. Gdy  , wektor
, wektor ma normę jednostkową i sam w sobie stanowi zbiór ortonormalny: nie ma innych wektorów, więc warunek ortogonalności jest trywialnie spełniony. Zbiór
ma normę jednostkową i sam w sobie stanowi zbiór ortonormalny: nie ma innych wektorów, więc warunek ortogonalności jest trywialnie spełniony. Zbiór jest zbiorem wszystkich skalarnych wielokrotności
jest zbiorem wszystkich skalarnych wielokrotności  , które są jednocześnie skalarnymi wielokrotnościami
, które są jednocześnie skalarnymi wielokrotnościami  (i odwrotnie). Wobec tego
(i odwrotnie). Wobec tego  Załóżmy teraz, że teza jest prawdziwa dla
Załóżmy teraz, że teza jest prawdziwa dla  . Wtedy możemy rzutować
. Wtedy możemy rzutować  na
na  :
: gdzie reszta
gdzie reszta  jest ortogonalna do
jest ortogonalna do  . Załóżmy, że
. Załóżmy, że  . Wtedy,
. Wtedy, Ponieważ, z założenia,
Ponieważ, z założenia,  dla dowolnego
dla dowolnego  , mamy, że
, mamy, że  dla dowolnego
dla dowolnego  , gdzie
, gdzie  są skalarami. Zatem,
są skalarami. Zatem, Innymi słowy, założenie, że
Innymi słowy, założenie, że  prowadzi do wniosku, że
prowadzi do wniosku, że  jest kombinacją liniową
jest kombinacją liniową  . Jest to jednak niemożliwe, gdyż jednym z założeń tej tezy jest to, że
. Jest to jednak niemożliwe, gdyż jednym z założeń tej tezy jest to, że  są liniowo niezależne. W konsekwencji musi być tak, że
są liniowo niezależne. W konsekwencji musi być tak, że  . Możemy zatem znormalizować resztę i zdefiniować wektor
. Możemy zatem znormalizować resztę i zdefiniować wektor , który ma normę jednostkową. Wiemy już, że
, który ma normę jednostkową. Wiemy już, że  jest ortogonalny do
jest ortogonalny do  . Wynika z tego, że również
. Wynika z tego, że również  jest ortogonalny do
jest ortogonalny do  . Zatem
. Zatem  jest zbiorem ortonormalnym. Weźmy teraz dowolny wektor
jest zbiorem ortonormalnym. Weźmy teraz dowolny wektor  , który można zapisać jako
, który można zapisać jako , gdzie
, gdzie  są skalarami. Ponieważ, z założenia,
są skalarami. Ponieważ, z założenia,  mamy, że równanie (2) można też zapisać jako
mamy, że równanie (2) można też zapisać jako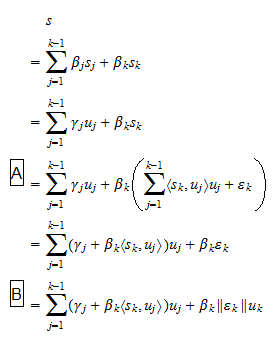 gdzie
gdzie  są skalarami, oraz: w kroku
są skalarami, oraz: w kroku  wykorzystaliśmy równanie (1); w kroku
wykorzystaliśmy równanie (1); w kroku  wykorzystaliśmy definicję
wykorzystaliśmy definicję  . Udowodniliśmy zatem, że każdy wektor, który można zapisać jako kombinację liniową
. Udowodniliśmy zatem, że każdy wektor, który można zapisać jako kombinację liniową  można również zapisać jako kombinację liniową
można również zapisać jako kombinację liniową  . Założenie (3) pozwala w całkowicie analogiczny sposób udowodnić, że jest odwrotnie:
. Założenie (3) pozwala w całkowicie analogiczny sposób udowodnić, że jest odwrotnie: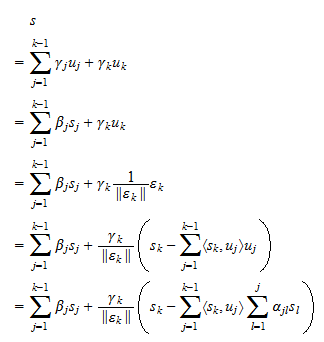 Innymi słowy, każda kombinacja liniowa
Innymi słowy, każda kombinacja liniowa  jest również kombinacją liniową
jest również kombinacją liniową  . Dowodzi to, że
. Dowodzi to, że  i kończy dowód.
i kończy dowód.
Każda przestrzeń produktu wewnętrznego ma ortonormalną podstawę
Następująca propozycja przedstawia ważną konsekwencję procesu Grama-Schmidta.
Propozycja Niech  będzie przestrzenią wektorową wyposażoną w iloczyn wewnętrzny
będzie przestrzenią wektorową wyposażoną w iloczyn wewnętrzny  . Jeśli
. Jeśli  ma skończony wymiar
ma skończony wymiar  , to istnieje ortonormalna podstawa
, to istnieje ortonormalna podstawa  dla
dla  .
.
Ponieważ  jest skończenie wymiarowy, istnieje co najmniej jedna podstawa dla
jest skończenie wymiarowy, istnieje co najmniej jedna podstawa dla  , składająca się z
, składająca się z  wektorów
wektorów  . Do tej podstawy możemy zastosować procedurę Grama-Schmidta i otrzymać zbiór ortonormalny
. Do tej podstawy możemy zastosować procedurę Grama-Schmidta i otrzymać zbiór ortonormalny  . Ponieważ
. Ponieważ  jest bazą, to rozciąga się na
jest bazą, to rozciąga się na  . Zatem
. Zatem 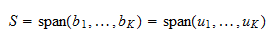
 jest ortonormalną bazą
jest ortonormalną bazą  .
.
Rozwiązane ćwiczenia
Poniżej znajdziesz kilka ćwiczeń z objaśnionymi rozwiązaniami.
Ćwiczenie 1
Rozważmy przestrzeń  wszystkich
wszystkich  wektorów mających rzeczywiste wpisy i iloczyn wewnętrzny
wektorów mających rzeczywiste wpisy i iloczyn wewnętrzny gdzie
gdzie  oraz
oraz  jest transpozycją
jest transpozycją  . Zdefiniuj wektor
. Zdefiniuj wektor
Normalizuj  .
.
Norma wektora  wynosi
wynosi Dlatego, normalizacja
Dlatego, normalizacja  wynosi
wynosi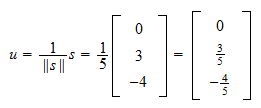
Ćwiczenie 2
Rozważmy przestrzeń  wszystkich
wszystkich  wektorów o rzeczywistych pozycjach i iloczynie wewnętrznym
wektorów o rzeczywistych pozycjach i iloczynie wewnętrznym gdzie
gdzie  . Rozważmy dwa liniowo niezależne wektory
. Rozważmy dwa liniowo niezależne wektory
Przekształćmy je w zbiór ortonormalny za pomocą procesu Grama-Schmidta.
Norma  wynosi
wynosi  Więc, pierwszy wektor ortonormalny to
Więc, pierwszy wektor ortonormalny to Iloczyn wewnętrzny
Iloczyn wewnętrzny  i
i  to
to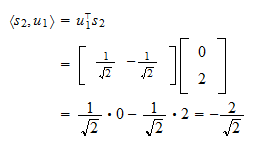 Rzut
Rzut  na
na  to
to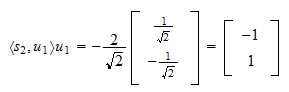 Reszta z rzutu to
Reszta z rzutu to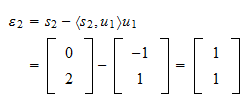 Norma tej reszty to
Norma tej reszty to a znormalizowana reszta to
a znormalizowana reszta to Tak więc, zbiór ortonormalny, którego szukaliśmy to
Tak więc, zbiór ortonormalny, którego szukaliśmy to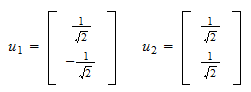
Jak cytować
Please cite as:
Taboga, Marco (2017). „Proces Grama-Schmidta”, Wykłady z algebry macierzy. https://www.statlect.com/matrix-algebra/Gram-Schmidt-process.
Leave a Reply