Mathematics for the Liberal Arts
Learning Outcomes
- Definiuj i zidentyfikuj samopodobieństwo w kształtach geometrycznych, roślinach, i formacjach geologicznych
- Generowanie kształtu fraktalnego biorąc pod uwagę inicjator i generator
- Skalowanie obiektu geometrycznego przez określony współczynnik skalowania używając relacji wymiaru skalowania
- Określanie wymiaru fraktalnego obiektu fraktalnego
Oprócz wizualnego samopodobieństwa, fraktale wykazują inne interesujące właściwości. Na przykład, zauważ, że każdy krok iteracji uszczelki Sierpińskiego usuwa jedną czwartą pozostałego obszaru. Jeśli ten proces jest kontynuowany w nieskończoność, skończylibyśmy w zasadzie usuwając cały obszar, co oznacza, że zaczęliśmy z dwuwymiarowym obszarem i jakoś skończylibyśmy z czymś mniejszym niż to, ale najwyraźniej więcej niż tylko jednowymiarową linią.
Aby zbadać ten pomysł, musimy omówić wymiar. Coś takiego jak linia jest jednowymiarowa; ma tylko długość. Każda krzywa jest jednowymiarowa. Rzeczy takie jak pudełka i koła są dwuwymiarowe, ponieważ mają długość i szerokość, opisując obszar. Obiekty takie jak pudełka i cylindry mają długość, szerokość i wysokość, opisując objętość, i są trójwymiarowe.
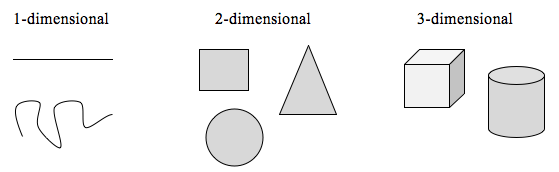
Pewne zasady dotyczą skalowania obiektów, związane z ich wymiarami.
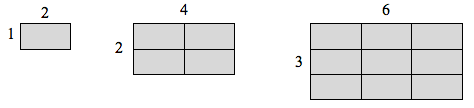
Gdybym miał linię o długości 1 i chciał przeskalować jej długość o 2, potrzebowałbym dwóch kopii oryginalnej linii. Gdybym miał linię o długości 1, i chciał przeskalować jej długość o 3, potrzebowałbym trzech kopii oryginału.
Gdybym miał prostokąt o długości 2 i wysokości 1, i chciał przeskalować jego długość i szerokość o 2, potrzebowałbym czterech kopii oryginalnego prostokąta. Gdybym chciał przeskalować długość i szerokość o 3, potrzebowałbym dziewięć kopii oryginalnego prostokąta.
Gdybym miał prostopadłościan o bokach długości 1 i chciał przeskalować jego długość i szerokość o 2, potrzebowałbym ośmiu kopii oryginalnego sześcianu. Gdybym chciał przeskalować długość i szerokość o 3, potrzebowałbym 27 kopii oryginalnego sześcianu.
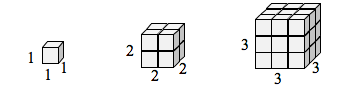
Zauważ, że w przypadku jednowymiarowym, potrzebne kopie = skala.
W przypadku dwuwymiarowym, potrzebne kopie = skala^{2}.
W przypadku trójwymiarowym, potrzebne kopie = skala^{3}.
Z tych przykładów, możemy wywnioskować wzór.
Relacja skalowanie-wymiar
Aby przeskalować kształt D-wymiarowy o współczynnik skalowania S, liczba potrzebnych kopii C oryginalnego kształtu będzie dana przez:
tekst{Kopie}=^{Scale}^{Dimension}}, czyli C=S^{D}
Przykład
Użyj zależności skalowanie-wymiar do wyznaczenia wymiaru uszczelki Sierpińskiego.
Załóżmy, że oryginalna uszczelka ma bok długości 1. Pokazana większa uszczelka jest dwa razy szersza i dwa razy wyższa, więc została przeskalowana o współczynnik 2.
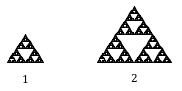
Zauważ, że do skonstruowania większej uszczelki potrzebne są 3 kopie oryginalnej uszczelki.
Korzystając z zależności skalowanie-wymiar C=S^{D}, otrzymujemy równanie 3=2^{D}.
Ponieważ 2^{1}=2 i 2^{2}=4, natychmiast widzimy, że D jest gdzieś pomiędzy 1 i 2; uszczelka jest więcej niż jednowymiarowym kształtem, ale zabraliśmy tak dużo obszaru, że jest teraz mniej niż dwuwymiarowa.
Rozwiązanie równania 3=2^{D} wymaga logarytmów. Jeśli uczyłeś się wcześniej o logarytmach, możesz sobie przypomnieć, jak rozwiązać to równanie (jeśli nie, przejdź do ramki poniżej i użyj tej formuły z klawiszem log na kalkulatorze):
Wybierz logarytm z obu stron.
3={{2}^{D}}
Użyj własności wykładników logarytmów.
log(3)=Lewy({{2}^{D}}}Prawy)
Podziel przez log(2).
log(3)=Dlogleft(2)
Wymiar uszczelki wynosi około 1,585.
D=frac{log(3)}{log(2)}approx1.585
Relacja skalowanie-wymiar, aby znaleźć wymiar
Aby znaleźć wymiar D fraktala, określ współczynnik skalowania S i liczbę potrzebnych kopii C oryginalnego kształtu, następnie użyj wzoru
D=frac{log(C)}{log(S)}
Try It
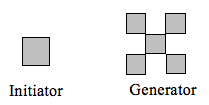
Określ wymiar fraktalny fraktala wytworzonego przy użyciu inicjatora i generatora.
W poniższym filmie prezentujemy działający przykład jak wyznaczyć wymiar uszczelki Sierpińskiego
.

Leave a Reply