Green’s Function

Generally speaking, funkcja Greena jest jądrem całkowym, które może być użyte do rozwiązywania równań różniczkowych z wielu rodzin, w tym prostszych przykładów, takich jak równania różniczkowe zwyczajne z warunkami początkowymi lub brzegowymi, jak również trudniejszych przykładów, takich jak niejednorodne równania różniczkowe cząstkowe (PDE) z warunkami brzegowymi. Ważne z wielu powodów, funkcje Greena pozwalają na wizualną interpretację oddziaływań związanych ze źródłem siły lub z ładunkiem skupionym w punkcie (Qin 2014), co czyni je szczególnie użytecznymi w dziedzinach matematyki stosowanej. W szczególności, metody funkcji Greena są szeroko stosowane w, np, fizyce i inżynierii.

Precyzyjniej, biorąc pod uwagę liniowy operator różniczkowy działający na zbiorze rozkładów nad podzbiorem pewnej przestrzeni euklidesowej , funkcja Greena w punkcie odpowiadającym jest dowolnym rozwiązaniem

(1)

gdzie oznacza funkcję delta. Motywacja do zdefiniowania takiej funkcji jest szeroka, ale mnożąc powyższą tożsamość przez funkcję i całkując względem otrzymujemy

(2)

Prawa strona sprowadza się jedynie do ze względu na własności funkcji delta, a ponieważ jest operatorem liniowym działającym tylko na , a nie na , lewą stronę można przepisać jako

(3)

Ta redukcja jest szczególnie przydatna przy rozwiązywaniu dla w równaniach różniczkowych postaci

(4)

gdzie powyższa arytmetyka potwierdza, że

(5)

i z czego wynika, że ma szczególną postać całkową

(6)

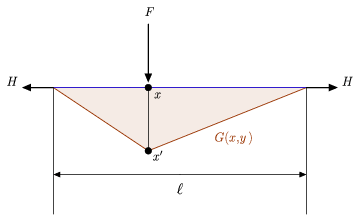
Powyższy rysunek ilustruje zarówno intuicyjną fizyczną interpretację funkcji Greena, jak i stosunkowo proste związane z nią równanie różniczkowe, z którym można porównać powyższą definicję (Hartmann 2013). W szczególności przedstawia on napiętą linę o długości zawieszoną pomiędzy dwiema ścianami, utrzymywaną w miejscu przez identyczną siłę poziomą przyłożoną na każdym z jej końców oraz obciążenie boczne umieszczone w pewnym punkcie wewnętrznym na linie. Niech będzie punktem odpowiadającym na ugiętej linie, załóżmy, że siła skierowana w dół jest stała, powiedzmy , i niech oznacza ugięcie liny. Odpowiada temu układowi fizycznemu równanie różniczkowe

(7)

dla z , układ, którego prostota pozwala na jednoznaczne zapisanie zarówno jego rozwiązania jak i funkcji Greena :

(8)

oraz

(9)

odpowiednio. Jak pokazano na powyższym rysunku, przemieszczona lina ma postać liniową w kawałku daną przez powyżej, potwierdzając tym samym twierdzenie, że funkcja Greena związana z tym układem reprezentuje działanie poziomej liny odpowiadające przyłożeniu siły .

Funkcja Greena przyjmująca parę argumentów jest czasami nazywana dwupunktową funkcją Greena. Jest to w przeciwieństwie do wielopunktowych funkcji Greena, które mają szczególne znaczenie w dziedzinie teorii wielu ciał.

Jako elementarny przykład funkcji dwupunktowej zdefiniowanej powyżej, rozważmy problem wyznaczenia potencjału generowanego przez rozkład ładunku, którego gęstość ładunku wynosi , przy czym zastosowanie równania Poissona i prawa Coulomba do potencjału w wytworzonego przez każdy element o ładunku daje rozwiązanie

(10)

który posiada, pod pewnymi warunkami, w obszarze, w którym . Ponieważ prawa strona może być traktowana jako operator całkowy przekształcający na , można przepisać to rozwiązanie w kategoriach funkcji Greena mającej postać

(11)

gdzie rozwiązanie można przepisać:

(12)

(Arfken 2012).

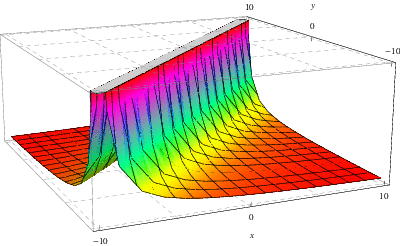
Powyższy rysunek przedstawia funkcję Greena związaną z rozwiązaniem równania – omówionego powyżej, gdzie tutaj, i , odpowiednio , jest wykreślona na osi -, odpowiednio -.

Nieco wyczerpującą listę funkcji Greena odpowiadających różnym równaniom różniczkowym prowadzi w Internecie Kevin Cole (Cole 2000).

W związku z mnogością literatury poświęconej funkcjom Greena, może pojawić się kilka różnych notacji i definicji, z których niektóre różnią się od powyższych, ale na ogół nie wpływają na istotne własności wyników. Na przykład, jak pokazuje powyższy przykład, niektórzy autorzy wolą oznaczać zmienne i wektorami i , aby podkreślić fakt, że są one elementami dla jakiegoś , które może być większe od 1 (Arfken 1985). Stosunkowo często spotyka się też definicję ze znakiem ujemnym, tak że definiuje się jako funkcję, dla której

(13)

ale ze względu na fakt, że te czysto fizyczne rozważania nie mają żadnego wpływu na matematykę leżącą u ich podstaw, ten punkt widzenia jest na ogół pomijany. Znanych jest również kilka innych notacji funkcji Greena, niektóre z nich obejmują użycie małej litery w miejsce (Stakgold 1979), jak również włączenie pionowej linii zamiast przecinka, np, (Duffy 2001).

W innych przypadkach literatura prezentuje definicje, które są ściśle związane z kontekstami, w których są prezentowane. Na przykład, niektórzy autorzy definiują funkcje Greena jako funkcje spełniające pewien zestaw warunków, np. istnienie na specjalnym rodzaju dziedziny, powiązanie z bardzo szczególnym operatorem różniczkowym , lub spełnienie ściśle określonego zestawu warunków brzegowych. Jeden z najczęstszych takich przykładów można znaleźć w notatkach np, Specka, gdzie funkcja Greena jest zdefiniowana tak, że spełnia dla punktów oraz dla wszystkich punktów leżących na granicy z (Speck 2011). Ta konkretna definicja przedstawia jądro całkowe odpowiadające rozwiązaniu uogólnionego równania Poissona i dlatego napotkałaby oczywiste ograniczenia przy adaptacji do bardziej ogólnych warunków. Z drugiej strony, takie przykłady nie są pozbawione zalet. W przypadku powyższego uogólnionego przykładu Poissona, na przykład, każda taka funkcja Greena może być podzielona tak, że

(14)

gdzie oraz dla regularnego laplacianu (Hartman 2013). W takich sytuacjach, jest znane jako fundamentalne rozwiązanie podstawowego równania różniczkowego, a jest znane jako jego rozwiązanie regularne; jako takie, i są czasami nazywane odpowiednio fundamentalną i regularną częścią .

Kilka podstawowych własności ogólnej funkcji Greena wynika natychmiast (lub prawie tak) z jej definicji i przenosi się na wszystkie szczególne przypadki. Na przykład, jeżeli jądro operatora jest nietrywialne, to może istnieć kilka funkcji Greena związanych z jednym operatorem; w rezultacie, należy zachować ostrożność odnosząc się do „funkcji” Greena. Funkcje Greena spełniają symetrię addytywną w swoich dwóch argumentach tak, że

(15)

gdzie jest zdefiniowane jako rozwiązanie równania

(16)

Tutaj jest addytywem . Bezpośrednim następstwem tego faktu jest to, że dla operatorów samoprzylegających , jest symetryczny:

(17)

Ta tożsamość jest często nazywana zasadą wzajemności i mówi, w kategoriach fizycznych, że odpowiedź w punkcie spowodowana przez jednostkowe źródło w punkcie jest taka sama jak odpowiedź w punkcie spowodowana przez jednostkową siłę w punkcie (Stakgold 1979).

Niezbędną własnością każdej funkcji Greena jest to, że zapewnia ona sposób opisu odpowiedzi rozwiązania arbitralnego równania różniczkowego na pewien rodzaj terminu źródłowego w obecności pewnej liczby warunków brzegowych (Arfken et al. 2012). Niektórzy autorzy uważają, że funkcja Greena pełni mniej więcej analogiczną rolę w teorii równań różniczkowych cząstkowych, jak szeregi Fouriera w rozwiązywaniu równań różniczkowych zwyczajnych (Mikula i Kos 2006).

W przypadku bardziej abstrakcyjnych scenariuszy istnieje szereg pojęć, które służą jako kontekstowe analogie do pojęcia funkcji Greena. Na przykład, w analizie funkcjonalnej często przydatne jest rozważenie tzw. uogólnionej funkcji Greena, która ma wiele analogicznych własności, gdy jest abstrakcyjnie zintegrowana z funkcjami, a nie z funkcjami. W rzeczy samej, takie uogólnienia doprowadziły do powstania całkowicie analogicznej gałęzi teoretycznej analizy PDE i same są przedmiotem wielu badań.