Gibbs Sampling

Podobnie jak inne metody MCMC, próbnik Gibbsa konstruuje łańcuch Markowa, którego wartości zbiegają się w kierunku rozkładu docelowego. Próbkowanie Gibbsa jest w rzeczywistości szczególnym przypadkiem algorytmu Metropolis-Hastings, w którym propozycje są zawsze akceptowane.

Aby to rozwinąć, załóżmy, że chcesz spróbować wielowymiarowego rozkładu prawdopodobieństwa.

Uwaga: Wielowymiarowy rozkład prawdopodobieństwa jest funkcją wielu zmiennych (np. 2 wymiarowy rozkład normalny).

Nie wiemy, jak bezpośrednio próbkować z tego ostatniego. Jednak dzięki pewnemu matematycznemu udogodnieniu, a może po prostu szczęściu, znamy prawdopodobieństwa warunkowe.

W tym miejscu pojawia się próbkowanie Gibbsa. Próbkowanie Gibbsa ma zastosowanie, gdy wspólny rozkład nie jest znany bezpośrednio lub trudno z niego pobierać próbki, ale warunkowy rozkład każdej zmiennej jest znany i łatwiej z niego pobierać próbki.

Zaczynamy od wybrania wartości początkowej dla zmiennych losowych X & Y. Następnie pobieramy próbki z warunkowego rozkładu prawdopodobieństwa X danego Y = Y⁰ oznaczanego p(X|Y⁰). W kolejnym kroku próbkujemy nową wartość Y warunkową na X¹, którą właśnie obliczyliśmy. Procedurę powtarzamy przez dodatkowe n – 1 iteracji, na przemian losując nową próbkę z warunkowego rozkładu prawdopodobieństwa X i warunkowego rozkładu prawdopodobieństwa Y, biorąc pod uwagę aktualną wartość drugiej zmiennej losowej.

Przyjrzyjrzyjmy się przykładowi. Załóżmy, że mamy następujące rozkłady prawdopodobieństwa potomnego i warunkowego.

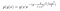
gdzie g(y) zawiera terminy, które nie zawierają x, a g(x) zawiera te, które nie zależą od y.

Nie znamy wartości C (stałej normalizującej). Znamy jednak warunkowe rozkłady prawdopodobieństwa. Możemy więc użyć próbkowania Gibbsa do przybliżenia rozkładu potomnego.

Uwaga: Prawdopodobieństwa warunkowe są w rzeczywistości rozkładami normalnymi i można je zapisać następująco.

Mając powyższe równania, przystępujemy do implementacji algorytmu próbkowania Gibbsa w Pythonie. Na początek importujemy następujące biblioteki.

import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
sns.set()

Zdefiniujemy funkcję dla rozkładu potomnego (zakładamy C=1).

f = lambda x, y: np.exp(-(x*x*y*y+x*x+y*y-8*x-8*y)/2.)

Następnie wykreślamy rozkład prawdopodobieństwa.

xx = np.linspace(-1, 8, 100)
yy = np.linspace(-1, 8, 100)
xg,yg = np.meshgrid(xx, yy)
z = f(xg.ravel(), yg.ravel())
z2 = z.reshape(xg.shape)
plt.contourf(xg, yg, z2, cmap='BrBG')

Teraz spróbujemy oszacować rozkład prawdopodobieństwa za pomocą Próbkowania Gibbsa. Jak wspomnieliśmy wcześniej, prawdopodobieństwa warunkowe są rozkładami normalnymi. Dlatego możemy je wyrazić w kategoriach mu i sigma.

W poniższym bloku kodu definiujemy funkcje dla mu i sigma, inicjalizujemy nasze zmienne losowe X & Y i ustawiamy N (liczbę iteracji).

N = 50000
x = np.zeros(N+1)
y = np.zeros(N+1)
x = 1.
y = 6.
sig = lambda z, i: np.sqrt(1./(1.+z*z))
mu = lambda z, i: 4./(1.+z*z)

Przechodzimy przez algorytm Gibbs Sampling.

for i in range(1, N, 2):
sig_x = sig(y, i-1)
mu_x = mu(y, i-1)
x = np.random.normal(mu_x, sig_x)
y = y
sig_y = sig(x, i)
mu_y = mu(x, i)
y = np.random.normal(mu_y, sig_y)
x = x

Na koniec wykreślamy wyniki.

plt.hist(x, bins=50);
plt.hist(y, bins=50);

plt.contourf(xg, yg, z2, alpha=0.8, cmap='BrBG')
plt.plot(x,y, '.', alpha=0.1)
plt.plot(x,y, c='r', alpha=0.3, lw=1)

Jak widzimy, rozkład prawdopodobieństwa uzyskany za pomocą algorytmu próbkowania Gibbsa dobrze przybliża rozkład docelowy.

Wniosek

Próbkowanie Gibbsa jest metodą Monte Carlo Markov Chain, która iteracyjnie losuje instancję z rozkładu każdej zmiennej, warunkowo od aktualnych wartości innych zmiennych w celu oszacowania złożonych rozkładów łącznych. W przeciwieństwie do algorytmu Metropolis-Hastings, zawsze akceptujemy propozycję. W ten sposób Gibbs Sampling może być znacznie bardziej wydajny.