Filtrowanie bilinearne i interpolacja bilinearna

Przyjrzyjrzyj się poniższemu obrazkowi. Czy potrafisz obliczyć wartości w punktach A,B i C?

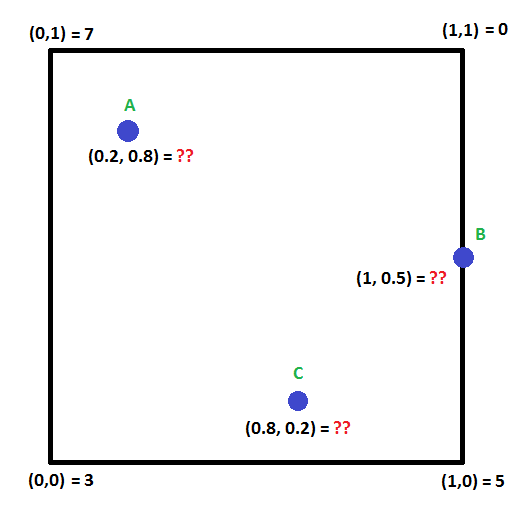
Jest na to technika zwana interpolacją bilinearną, która rozszerza ideę interpolacji liniowej na dwa wymiary.

Aby obliczyć interpolację bilinearną, po prostu wykonujesz interpolację liniową na jednej osi, a następnie na drugiej.

Sprawdź te przykłady:

Punkt A
Punkt A ma współrzędne (0,2,0,8). Zacznijmy od osi X.

Po pierwsze, wykonamy interpolację w poprzek górnej części kwadratu na osi X. Oznacza to, że musimy przejść 0,2 (20%) drogi od 7 do 0. To 0,2 jest naszą współrzędną osi x. Aby to obliczyć robimy tak:
7 + (0-7) * 0.2 = 5.6

Następnie wykonamy interpolację w poprzek dolnej części kwadratu na osi X. Tak więc podobnie jak powyżej, przejdziemy 0,2 (20%) drogi od 3 do 5. Aby to obliczyć, zrobimy tak:
3 + (5-3) * 0.2 = 3.4

Teraz, gdy mamy interpolację w poprzek naszej osi X, musimy interpolować w poprzek naszej osi Y. Zamierzamy teraz przejść 0,8 (80%) drogi od naszej dolnej wartości (wartość Y = 0), do naszej górnej wartości (wartość Y = 1). Dolna wartość to dolna interpolacja, którą wykonaliśmy (3.4), a górna wartość to górna interpolacja, którą wykonaliśmy (5.6).

Więc musimy przejść 0.8 (80%) drogi od 3.4 do 5.6. Aby to obliczyć robimy tak:
3,4 + (5,6 – 3,4) * 0,8 = 5,16

Więc, wartość w punkcie A wynosi 5,16. Poniższy obraz powinien pomóc w wizualnym wyjaśnieniu procesu, przez który przeszliśmy.

Punkt B

Punkt B ma współrzędne (1.0,0.5).

Zacznijmy ponownie od interpolacji na osi X (chociaż mógłbyś łatwo zacząć od Y, gdybyś chciał! Skończyłbyś z tym samym wynikiem).

Dokonując interpolacji osi X w poprzek góry, musimy przejść 1.0 (100%) drogi od 7 do 0. Jestem pewien, że możesz zgadnąć, jaka jest odpowiedź, ale tutaj jest ona obliczona:
7 + (0-7) * 1.0 = 0

Podobnie, zróbmy interpolację osi X w poprzek dołu. Musimy przejść 1.0 (100%) drogi od 3 do 5.
3 + (5-3) * 1.0 = 5

Następnie następuje interpolacja osi Y. Musimy przejść 0,5 (50%) drogi od 5 do 0.
5 + (0-5) * 0,5 = 2,5

Tutaj idziemy, wartość w punkcie B wynosi 2,5. To również powinno mieć sens, patrząc na wykres. Jest to w zasadzie interpolacja liniowa 1d między 5 i 0, i jest w połowie drogi między nimi, więc intuicyjnie odpowiedź 2,5 powinna mieć sens.

Punkt C

Punkt C ma współrzędne (0,8,0,2).

Jeszcze raz wykonajmy interpolację osi X w poprzek górnej części pudełka. Musimy przejść 0,8 (80%) drogi od 7 do 0.
7 + (0-7) * 0,8 = 1,4

Następnie musimy wykonać interpolację osi x w poprzek dolnej części pudełka. Musimy przejść 0,8 (80%) drogi od 3 do 5.
3 + (5-3) * 0,8 = 4,6

Na koniec interpolacja osi y. Musimy przejść o 0,2 (20%) od 4,6 do 1,4.
4,6 + (1,4-4,6) * 0,2 = 3,96

Wartość punktu C wynosi 3.96

Filtrowanie dwuliniowe

Choć interpolacja dwuliniowa jest przydatna, jeśli masz siatkę danych, które chcesz interpolować (np. pole wysokości, które reprezentuje teren?!), gdzie to naprawdę błyszczy w rozwoju gier jest w dwuliniowym filtrowaniu tekstur.

Podstawowo, gdy masz współrzędną tekstury, która nie jest idealnie zgodna ze środkiem piksela w teksturze (ponieważ jest reszta), używa ona ułamkowej części współrzędnej w tym pikselu, aby wykonać interpolację bilinearną pomiędzy 4 zaangażowanymi pikselami, aby uzyskać ostateczny kolor piksela. Wykonuje interpolację bilinearną na każdym z kanałów: Red, Green, Blue i Alpha.

Efekt końcowy jest całkiem niezły! Sprawdź poniższy obrazek, aby zobaczyć go w akcji na teksturze, którą za bardzo powiększyliśmy. Lewa strona używa filtrowania bilinearnego, podczas gdy prawa nie, i po prostu pokazuje najbliższy piksel.

W konsekwencji, filtrowanie bilinearne tekstury musi wykonać 4 odczyty pikseli, aby móc interpolować między nimi, zamiast pojedynczego odczytu pikseli, jak w przypadku próbkowania najbliższego piksela. Więcej odczytów pikseli = większy narzut, i nie jest tak tanie (obliczeniowo) w użyciu.

Linki

Dla niektórych ludzi, którzy to czytają, ta informacja jest dość podstawowa i możesz się zastanawiać dlaczego zawracam sobie głowę pisaniem o tym. Zajrzyj do następnego posta, gdzie znajdziesz coś dziwnego związanego z filtrowaniem biliniowym. To było potrzebne jako krok do następnej rzeczy, którą chcę wam pokazać 😛

Wikipedia: Linear Interpolation

Wikipedia: Bilinear Interpolation

Wikipedia: Filtrowanie bilinearne

Ciemna strona filtrowania bilinearnego

Sprawdź te łącza, aby dowiedzieć się więcej o niektórych niedociągnięciach (i obejściach) sprzętowego próbkowania bilinearnego:
iq: interpolacja sprzętowa
iq: ulepszona interpolacja tekstur