Część 14 : Iloczyn kropkowy i iloczyn Hadamarda

Oprócz omówionego wcześniej mnożenia macierzy, wektory można mnożyć jeszcze dwiema metodami : Iloczyn kropkowy i iloczyn Hadamarda. Wyniki uzyskane z obu metod są różne.

Elementy odpowiadające temu samemu wierszowi i kolumnie są mnożone razem, a produkty są dodawane w taki sposób, że wynik jest skalarem.

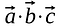
W przeciwieństwie do mnożenia macierzy wynik iloczynu punktowego nie jest innym wektorem ani macierzą, jest skalarem.

Porządek wektorów nie ma znaczenia dla iloczynu punktowego, po prostu liczba elementów w obu wektorach powinna być równa.

Sformułowanie geometryczne iloczynu punktowego to

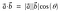
Iloczyn punktowy jest również nazywany iloczynem wewnętrznym lub iloczynem skalarnym.

Przerzut wektora

Zakładając, że mamy dwa wektory c i d, odjęte od siebie przez kąt, phi(Ф).

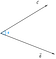
Teraz, rzut wektora c na wektor d można przedstawić jako

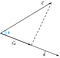
Z rysunku możemy wywnioskować, że rzut jest równy składowej poziomej wektora c względem kąta phi(Ф).

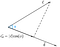
To się nazywa rzutowanie skalarne.Aby znaleźć rzut wektora c na wektor d, musimy pomnożyć rzut skalarny przez wektor jednostkowy d.

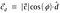
Substytucja wartości wektora jednostkowego d.

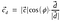
Tak więc, dot product could also be represented as

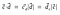
Projekcje mają szerokie zastosowanie w algebrze liniowej i uczeniu maszynowym (Support Vector Machine(SVM) jest algorytmem uczenia maszynowego, używanym do klasyfikacji danych).

Iloczyn Hadamarda (Element -wise Multiplication)

Iloczyn Hadamarda dwóch wektorów jest bardzo podobny do dodawania macierzy, elementy odpowiadające tym samym wierszom i kolumnom danych wektorów/macierzy są mnożone razem, aby utworzyć nowy wektor/macierz.

Nazwa pochodzi od nazwiska francuskiego matematyka, Jacques’a Hadamarda.

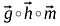
Kolejność mnożonych macierzy/wektorów powinna być taka sama i wynikowa macierz również będzie tego samego rzędu.

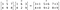
Iloczyn Kadamarda jest używany w technikach kompresji obrazów, takich jak JPEG. Jest on również znany jako iloczyn Schura od nazwiska niemieckiego matematyka Issai Schura.

Iloczyn Hadamarda jest używany w komórkach LSTM (Long Short-Term Memory) w rekurencyjnych sieciach neuronowych (RNN).