Co to jest geometria analityczna?
Co to jest geometria analityczna?
Geometria analityczna jest gałęzią algebry, która służy do modelowania obiektów geometrycznych – punkty, linie (proste) i okręgi są najbardziej podstawowymi z nich. Geometria analityczna jest wielkim wynalazkiem Kartezjusza i Fermata.
W geometrii analitycznej płaszczyzny, punkty są zdefiniowane jako uporządkowane pary liczb, powiedzmy, (x, y), podczas gdy linie proste są z kolei zdefiniowane jako zbiory punktów, które spełniają równania liniowe, patrz doskonałe ekspozycje przez D. Pedoe lub D. Brannan et al. Z punktu widzenia geometrii analitycznej, aksjomaty geometryczne są pochodnymi twierdzeniami. Na przykład, dla dowolnych dwóch różnych punktów (x1, y1) i (x2, y2) istnieje jedna prosta ax + by + c = 0, która przechodzi przez te punkty. Jej współczynniki a, b, c można znaleźć (aż do stałego współczynnika) z liniowego układu dwóch równań
| ax1 + by1 + c = 0 ax2 + by2 + c = 0, |
lub bezpośrednio z równania wyznacznika
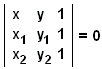 |
Jednakże żadna teoria aksjomatyczna nie może uciec od używania elementów nieokreślonych. W teorii zbiorów, która leży u podstaw znacznej części matematyki, a w szczególności geometrii analitycznej, najbardziej podstawowe pojęcie zbioru pozostaje niezdefiniowane.
Geometria trójwymiarowej przestrzeni jest modelowana za pomocą trójek liczb (x, y, z), a trójwymiarowe równanie liniowe ax + by + cz + d = 0 definiuje płaszczyznę. Ogólnie rzecz biorąc, geometria analityczna zapewnia wygodne narzędzie do pracy w wyższych wymiarach.
W ramach geometrii analitycznej można (i robi) modelować geometrie nieeuklidesowe, jak również. Na przykład, w płaszczyznowej geometrii rzutowej punkt jest trójką jednorodnych współrzędnych (x, y, z), nie wszystkich 0, takich, że
| (tx, ty, tz) = (x, y, z), |
dla wszystkich t ≠ 0, zaś prosta jest opisana równaniem jednorodnym
| ax + bx + cz = 0. |
W geometrii analitycznej przekroje stożkowe są definiowane przez równania drugiego stopnia:
| ax² + bxy + cy² + dx + ey + f = 0. |
Ta część geometrii analitycznej, która zajmuje się głównie równaniami liniowymi, nazywa się algebrą liniową.
Kartezjańska geometria analityczna to geometria, w której osie x = 0 i y = 0 są prostopadłe.
Składowe n-tupli x = (x1, …, xn) są znane jako jej współrzędne. Gdy n = 2 lub n = 3, pierwsza współrzędna jest nazywana odciętą, a druga rzędną.
- D. A. Brannan, M. F. Esplen, J. J. Gray, Geometry, Cambridge University Press, 2002
- D. Pedoe, Geometry: A Comprehensive Course, Dover, 1988
|Kontakt||Strona tytułowa|||Zawartość||Geometria||Up|
Copyright © 1996-2018 Aleksander Bogomolny
Leave a Reply