A Brief Introduction to Differential Privacy
.
Aaruran Elamurugaiyan
Prywatność można określić ilościowo. Jeszcze lepiej, możemy uszeregować strategie chroniące prywatność i powiedzieć, która z nich jest bardziej efektywna. Jeszcze lepiej, możemy zaprojektować strategie, które są odporne nawet na hakerów, którzy mają informacje pomocnicze. I jakby tego było mało, możemy robić wszystkie te rzeczy jednocześnie. Te rozwiązania, a nawet więcej, znajdują się w probabilistycznej teorii zwanej prywatnością różnicową.
Oto kontekst. Zajmujemy się (lub zarządzamy) wrażliwą bazą danych i chcielibyśmy udostępnić publicznie niektóre statystyki z tych danych. Musimy jednak zapewnić, że nie jest możliwe dla przeciwnika, aby odwrócić inżynierię wrażliwych danych z tego, co wydaliśmy. Przeciwnik w tym przypadku to strona, która ma zamiar ujawnić lub poznać przynajmniej niektóre z naszych wrażliwych danych. Zróżnicowana prywatność może rozwiązać problemy, które powstają, gdy te trzy składniki – wrażliwe dane, kuratorzy, którzy muszą udostępnić statystyki i przeciwnicy, którzy chcą odzyskać wrażliwe dane – są obecne (patrz rysunek 1). Ta inżynieria wsteczna jest rodzajem naruszenia prywatności.

Ale jak trudno jest naruszyć prywatność? Czy anonimizacja danych nie byłaby wystarczająco dobra? Jeśli masz informacje pomocnicze z innych źródeł danych, anonimizacja nie wystarczy. Na przykład w 2007 roku Netflix opublikował zbiór danych z ocenami użytkowników w ramach konkursu mającego na celu sprawdzenie, czy ktoś może prześcignąć ich algorytm filtrowania kolaboracyjnego. Zbiór danych nie zawierał informacji umożliwiających identyfikację osób, ale badacze nadal byli w stanie naruszyć prywatność; odzyskali 99% wszystkich danych osobowych, które zostały usunięte ze zbioru danych. W tym przypadku, badacze naruszyli prywatność używając pomocniczych informacji z IMDB.
Jak ktokolwiek może bronić się przed przeciwnikiem, który ma nieznaną i prawdopodobnie nieograniczoną pomoc ze świata zewnętrznego? Różnicowa prywatność oferuje rozwiązanie. Algorytmy różnicowo-prywatne są odporne na ataki adaptacyjne, które wykorzystują informacje pomocnicze. Algorytmy te polegają na włączeniu losowego szumu do mieszanki tak, że wszystko, co otrzymuje przeciwnik staje się hałaśliwe i nieprecyzyjne, a więc znacznie trudniej jest naruszyć prywatność (jeśli jest to w ogóle wykonalne).
Noisy Counting
Spójrzmy na prosty przykład wstrzykiwania szumu. Załóżmy, że zarządzamy bazą danych ratingów kredytowych (podsumowaną przez Tabelę 1).
Na potrzeby tego przykładu załóżmy, że adwersarz chce poznać liczbę osób, które mają złą ocenę kredytową (czyli 3). Dane są wrażliwe, więc nie możemy ujawnić prawdy podstawowej. Zamiast tego użyjemy algorytmu, który zwróci nam prawdę podstawową, N = 3, plus trochę losowego szumu. Ta podstawowa idea (dodanie losowego szumu do prawdy podstawowej) jest kluczowa dla prywatności różnicowej. Powiedzmy, że wybieramy liczbę losową L z rozkładu Laplace’a o zerowym środku i odchyleniu standardowym 2. Zwracamy N+L. Wyjaśnimy wybór odchylenia standardowego za kilka akapitów. (Jeśli nie słyszałeś o rozkładzie Laplace’a, zobacz rysunek 2). Algorytm ten będziemy nazywać „hałaśliwym liczeniem”.
Jeśli mamy zamiar zgłosić bezsensowną, zaszumioną odpowiedź, to jaki jest sens tego algorytmu? Odpowiedź jest taka, że pozwala on nam osiągnąć równowagę między użytecznością a prywatnością. Chcemy, aby ogół społeczeństwa zyskał pewną użyteczność z naszej bazy danych, nie narażając żadnych wrażliwych danych dla ewentualnego przeciwnika.
Co właściwie otrzymałby przeciwnik? Odpowiedzi są przedstawione w Tabeli 2.

Pierwsza odpowiedź, jaką otrzymuje adwersarz, jest bliska, ale nie równa prawdzie podstawowej. W tym sensie przeciwnik jest oszukany, użyteczność jest zapewniona, a prywatność jest chroniona. Ale po wielu próbach, będą w stanie oszacować prawdę gruntową. Ta „estymacja z powtarzających się zapytań” jest jednym z podstawowych ograniczeń prywatności różnicowej. Jeśli adwersarz może wykonać wystarczająco dużo zapytań do różnie prywatnej bazy danych, nadal może oszacować wrażliwe dane. Innymi słowy, przy coraz większej liczbie zapytań, prywatność zostaje naruszona. Tabela 2 empirycznie demonstruje to naruszenie prywatności. Jednak, jak widać, 90% przedział ufności z tych 5 zapytań jest dość szeroki; oszacowanie nie jest jeszcze bardzo dokładne.
Jak dokładne może być to oszacowanie? Spójrz na rysunek 3, na którym uruchomiliśmy symulację kilka razy i wykreśliliśmy wyniki .

Każda pionowa linia ilustruje szerokość 95% przedziału ufności, a punkty wskazują średnią z próbkowanych danych przeciwnika. Zauważ, że te wykresy mają logarytmiczną oś poziomą, i że szum jest pobierany z niezależnych i identycznie rozłożonych zmiennych losowych Laplace. Ogólnie rzecz biorąc, średnia jest bardziej zaszumiona przy mniejszej liczbie zapytań (ponieważ rozmiary próbek są małe). Zgodnie z oczekiwaniami, przedziały ufności stają się węższe, gdy przeciwnik wykonuje więcej zapytań (ponieważ wielkość próby rośnie, a szum uśrednia się do zera). Już po samym przejrzeniu wykresu widać, że potrzeba około 50 zapytań, aby dokonać przyzwoitego oszacowania.
Zastanówmy się nad tym przykładem. Przede wszystkim, poprzez dodanie losowego szumu, utrudniliśmy przeciwnikowi naruszenie prywatności. Po drugie, zastosowana przez nas strategia ukrywania była prosta do zaimplementowania i zrozumienia. Niestety, przy coraz większej liczbie zapytań, adwersarz był w stanie przybliżyć prawdziwą liczbę.
Jeśli zwiększymy wariancję dodanego szumu, możemy lepiej bronić naszych danych, ale nie możemy po prostu dodać dowolnego szumu Laplace’a do funkcji, którą chcemy ukryć. Powodem jest to, że ilość szumu, który musimy dodać, zależy od czułości funkcji, a każda funkcja ma swoją własną czułość. W szczególności, funkcja liczenia ma czułość równą 1. Przyjrzyjmy się, co oznacza czułość w tym kontekście.
Czułość i mechanizm Laplace’a
Dla funkcji:
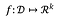
czułość f wynosi:
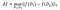
na zbiorach danych D₁, D₂ różniących się co najwyżej jednym elementem .
Powyższa definicja jest dość matematyczna, ale nie jest tak zła, jak się wydaje. Z grubsza rzecz biorąc, czułość funkcji jest największą możliwą różnicą, jaką jeden wiersz może mieć na wynik tej funkcji, dla dowolnego zestawu danych. Na przykład, w naszym zabawkowym zbiorze danych, liczenie liczby wierszy ma czułość 1, ponieważ dodanie lub usunięcie pojedynczego wiersza z dowolnego zbioru danych zmieni liczbę o co najwyżej 1.
Jako inny przykład, załóżmy, że myślimy o „liczeniu zaokrąglonym w górę do wielokrotności 5”. Ta funkcja ma czułość 5, a my możemy to dość łatwo pokazać. Jeśli mamy dwa zbiory danych o rozmiarze 10 i 11, różnią się one w jednym wierszu, ale „counts rounded up to a multiple of 5” to odpowiednio 10 i 15. W rzeczywistości, pięć jest największą możliwą różnicą, jaką ta przykładowa funkcja może wytworzyć. Dlatego jej czułość wynosi 5.
Obliczanie czułości dla arbitralnej funkcji jest trudne. Znaczna ilość wysiłków badawczych jest poświęcona na szacowanie czułości, poprawę szacunków czułości i obejście obliczania czułości .
Jak czułość odnosi się do hałaśliwego liczenia? Nasza strategia hałaśliwego liczenia wykorzystuje algorytm zwany mechanizmem Laplace’a, który z kolei opiera się na wrażliwości funkcji, którą przesłania. W Algorytmie 1 mamy naiwną pseudokodową implementację mechanizmu Laplace’a .
Algorytm 1
Wejście: Funkcja F, Wejście X, Poziom prywatności ϵ
Wyjście: A Noisy Answer
Compute F (X)
Compute sensitivity of of of F : S
Draw noise L from a Laplace distribution with variance:
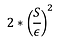
Wróć F(X) + L
Im większa czułość S, tym głośniejsza będzie odpowiedź. Liczenie ma czułość tylko 1, więc nie musimy dodawać dużo szumu, aby zachować prywatność.
Zauważ, że mechanizm Laplace’a w algorytmie 1 zużywa parametr epsilon. Będziemy odnosić się do tej wielkości jako do utraty prywatności przez mechanizm i jest ona częścią najbardziej centralnej definicji w dziedzinie prywatności różnicowej: epsilon-differential privacy. Dla zilustrowania, jeśli przypomnimy sobie nasz wcześniejszy przykład i użyjemy trochę algebry, możemy zobaczyć, że nasz szumiący mechanizm liczenia ma epsilon-różniczkową prywatność, z epsilonem 0,707. Dostrajając epsilon, kontrolujemy hałaśliwość naszego hałaśliwego liczenia. Wybranie mniejszego epsilonu daje bardziej hałaśliwe wyniki i lepsze gwarancje prywatności. Jako odniesienie, Apple używa epsilon równego 2 w różnie prywatnej autokorekcie klawiatury
Liczba epsilon jest sposobem, w jaki prywatność różnicowa może zapewnić rygorystyczne porównania pomiędzy różnymi strategiami. Formalna definicja epsilon-differential privacy jest nieco bardziej matematycznie zaangażowana, więc celowo pominąłem ją w tym wpisie na blogu. Więcej na ten temat można przeczytać w opracowaniu Dworka na temat prywatności różnicowej .
Jak pamiętasz, przykład hałaśliwego liczenia miał epsilon 0,707, co jest dość małe. Ale wciąż naruszyliśmy prywatność po 50 zapytaniach. Dlaczego? Ponieważ wraz ze wzrostem liczby zapytań rośnie budżet prywatności, a zatem gwarancja prywatności jest gorsza.
Budżet prywatności
Ogólnie rzecz biorąc, straty prywatności kumulują się. Gdy dwie odpowiedzi są zwracane do adwersarza, całkowita strata prywatności jest dwukrotnie większa, a gwarancja prywatności jest o połowę mniejsza. Ta kumulatywna własność jest konsekwencją twierdzenia o kompozycji. W istocie, z każdym nowym zapytaniem uwalniane są dodatkowe informacje o wrażliwych danych. Stąd, twierdzenie o składzie ma pesymistyczny pogląd i zakłada najgorszy scenariusz: taka sama ilość wycieku zdarza się z każdą nową odpowiedzią. Dla silnych gwarancji prywatności, chcemy, aby utrata prywatności była mała. Tak więc w naszym przykładzie, w którym mamy utratę prywatności na poziomie trzydziestu pięciu (po 50 zapytaniach do naszego mechanizmu liczenia szumów Laplace’a), odpowiednia gwarancja prywatności jest krucha.
Jak działa prywatność różnicowa, jeśli utrata prywatności rośnie tak szybko? Aby zapewnić sensowną gwarancję prywatności, kuratorzy danych mogą wymusić maksymalną utratę prywatności. Jeśli liczba zapytań przekroczy ten próg, wówczas gwarancja prywatności staje się zbyt słaba i kurator przestaje odpowiadać na zapytania. Maksymalna utrata prywatności nazywana jest budżetem prywatności . Możemy myśleć o każdym zapytaniu jako o „wydatku” na prywatność, który powoduje przyrostową utratę prywatności. Strategia używania budżetów, wydatków i strat jest trafnie znana jako rachunkowość prywatności .
Rachunkowość prywatności jest efektywną strategią obliczania utraty prywatności po wielu zapytaniach, ale nadal może zawierać twierdzenie o kompozycji. Jak zauważono wcześniej, twierdzenie o kompozycji zakłada najgorszy scenariusz. Innymi słowy, istnieją lepsze alternatywy.
Deep Learning
Deep learning to poddziedzina uczenia maszynowego, która odnosi się do szkolenia głębokich sieci neuronowych (DNNs) w celu oszacowania nieznanych funkcji . (Na wysokim poziomie, DNN jest sekwencją afinicznych i nieliniowych przekształceń mapujących pewną n-wymiarową przestrzeń na przestrzeń m-wymiarową). Jej zastosowania są bardzo szerokie i nie ma potrzeby ich tutaj powtarzać. Zbadamy, jak prywatnie trenować głęboką sieć neuronową.
Głębokie sieci neuronowe są zazwyczaj trenowane przy użyciu wariantu stochastycznego zejścia gradientowego (SGD). Abadi et al. wymyślili zachowującą prywatność wersję tego popularnego algorytmu, powszechnie nazywaną „prywatnym SGD” (lub PSGD). Rysunek 4 ilustruje moc ich nowatorskiej techniki. Abadi et al. wymyślili nowe podejście: księgowego momentów. Podstawową ideą księgowego momentów jest akumulacja wydatków na prywatność poprzez ujęcie utraty prywatności jako zmiennej losowej i wykorzystanie funkcji generujących momenty, aby lepiej zrozumieć rozkład tej zmiennej (stąd nazwa). Pełne szczegóły techniczne są poza zakresem wstępnego wpisu na blogu, ale zachęcamy do przeczytania oryginalnego papieru, aby dowiedzieć się więcej.

Myślenie końcowe
Przeglądaliśmy teorię prywatności różnicowej i zobaczyliśmy, jak można ją wykorzystać do ilościowego określenia prywatności. Przykłady w tym poście pokazują, jak podstawowe idee mogą być zastosowane i jaki jest związek między zastosowaniem a teorią. Ważne jest, aby pamiętać, że gwarancje prywatności pogarszają się wraz z wielokrotnym użyciem, więc warto pomyśleć o tym, jak to złagodzić, czy to za pomocą budżetowania prywatności, czy innych strategii. Możesz zbadać to zjawisko, klikając to zdanie i powtarzając nasze eksperymenty. Wciąż pozostaje wiele pytań, na które nie udzieliliśmy odpowiedzi, a także bogata literatura do zbadania – zobacz odnośniki poniżej. Zachęcamy do dalszej lektury.
Cynthia Dwork. Differential privacy: A survey of results. International Conference on Theory and Applications of Models of Computation, 2008.
Wikipedia Contributors. Rozkład Laplace’a, lipiec 2018.
Aaruran Elamurugaiyan. Plots demonstrating standard error of differentially private responses over number of queries., August 2018.
Benjamin I. P. Rubinstein and Francesco Alda. Pain-free random differential privacy with sensitivity sampling. In 34th International Conference on Machine Learning (ICML’2017) , 2017.
Cynthia Dwork and Aaron Roth. The algorithmic foundations of differential privacy . Now Publ., 2014.
Martin Abadi, Andy Chu, Ian Goodfellow, H. Brendan Mcmahan, Ilya Mironov, Kunal Talwar, and Li Zhang. Deep learning with differential privacy. Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security – CCS16 , 2016.
Frank D. McSherry. Privacy integrated queries: An extensible platform for privacy-preserving data analysis. In Proceedings of the 2009 ACM SIGMOD International Conference on Management of Data , SIGMOD ’09, pages 19-30, New York, NY, USA, 2009. ACM.
Wikipedia Contributors. Deep Learning, sierpień 2018.
Leave a Reply