9.5 – Identyfikacja wpływowych punktów danych

W tym rozdziale poznamy następujące dwie miary służące do identyfikacji wpływowych punktów danych:

• Różnica w dopasowaniu (DFFITS)
• Odległości Cooka

Podstawowa idea każdej z tych miar jest taka sama, a mianowicie usuwamy obserwacje po kolei, za każdym razem ponownie dopasowując model regresji do pozostałych n-1 obserwacji. Następnie porównujemy wyniki z wykorzystaniem wszystkich n obserwacji z wynikami z usuniętą i-tą obserwacją, aby zobaczyć, jak duży wpływ na analizę ma dana obserwacja. Analizując w ten sposób, jesteśmy w stanie ocenić potencjalny wpływ każdego punktu danych na analizę regresji.

Różnica w dopasowaniach (DFFITS)

Różnica w dopasowaniach dla obserwacji i, oznaczana jako DFFITSi, jest zdefiniowana jako:

Jak widać, licznik mierzy różnicę w przewidywanych odpowiedziach uzyskanych, gdy i-ty punkt danych jest włączony i wyłączony z analizy. Mianownik jest szacowanym odchyleniem standardowym różnicy w przewidywanych odpowiedziach. Dlatego różnica w dopasowaniu określa liczbę standardowych odchyleń, o jaką zmienia się dopasowana wartość, gdy i-ty punkt danych jest pominięty.

Obserwacja jest uważana za wpływową, jeśli wartość bezwzględna jej wartości DFFITS jest większa niż:

gdzie, jak zawsze, n = liczba obserwacji i k = liczba warunków predyktora (tj. liczba parametrów regresji z wyłączeniem punktu przecięcia). Należy pamiętać, że nie jest to sztywna reguła, a jedynie wskazówka! Nietrudno znaleźć różnych autorów stosujących nieco inne wytyczne. Dlatego często preferuję znacznie bardziej subiektywne wytyczne, np. punkt danych jest uznawany za wpływowy, jeśli wartość bezwzględna jego wartości DFFITS wyróżnia się na tle innych wartości DFFITS. Oczywiście, jest to osąd jakościowy, być może taki, jaki powinien być, ponieważ wartości odstające z samej swojej natury są wielkościami subiektywnymi.

Przykład #2 (ponownie). Sprawdźmy różnicę w miarach dopasowania dla tego zestawu danych (influence2.txt):

Regresja y na x i zapytanie o różnicę w dopasowaniach, otrzymujemy następujące dane wyjściowe oprogramowania:

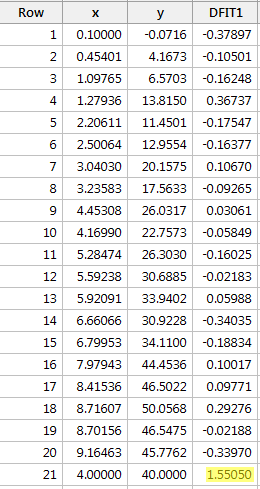
Używając obiektywnej wytycznej zdefiniowanej powyżej, uznajemy punkt danych za wpływowy, jeśli wartość bezwzględna jego wartości DFFITS jest większa niż:

Tylko jeden punkt danych – czerwony – ma wartość DFFITS, której wartość bezwzględna (1.55050) jest większa niż 0,82. Dlatego, opierając się na tej wytycznej, uznalibyśmy czerwony punkt danych za wpływowy.

Przykład #3 (ponownie). Sprawdźmy różnicę w miarach dopasowania dla tego zestawu danych (influence3.txt):

Regresja y na x i zapytanie o różnicę w dopasowaniach, otrzymujemy następujące dane wyjściowe oprogramowania:

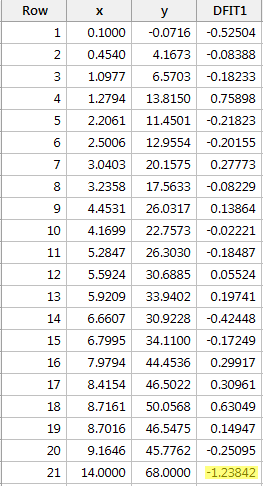
Używając obiektywnej wytycznej zdefiniowanej powyżej, uznajemy punkt danych za wpływowy, jeśli wartość bezwzględna jego wartości DFFITS jest większa niż:

Tylko jeden punkt danych – czerwony – ma wartość DFFITS, której wartość bezwzględna (1.23841) jest większa niż 0,82. Dlatego, w oparciu o tę wskazówkę, uznamy czerwony punkt danych za wpływowy.

Gdy studiowaliśmy ten zestaw danych na początku tej lekcji, zdecydowaliśmy, że czerwony punkt danych nie miał aż tak dużego wpływu na analizę regresji. Jednak tutaj różnica w miarach dopasowania sugeruje, że jest on rzeczywiście wpływowy. Co się tutaj dzieje? Wszystko sprowadza się do uznania, że wszystkie miary w tej lekcji są tylko narzędziami, które oznaczają potencjalnie wpływowe punkty danych dla analityka danych. W końcu, analityk powinien przeanalizować zestaw danych dwukrotnie – raz z zaznaczonymi punktami danych i raz bez nich. Jeśli punkty danych znacząco zmieniają wynik analizy regresji, wówczas badacz powinien zgłosić wyniki obu analiz.

Nawiasem mówiąc, w tym przykładzie, jeśli użyjemy bardziej subiektywnej wskazówki, czy wartość bezwzględna wartości DFFITS wystaje jak bolący kciuk, prawdopodobnie nie uznamy czerwonego punktu danych za wpływowy. W końcu, następna największa wartość DFFITS (w wartości bezwzględnej) wynosi 0,75898. Ta wartość DFFITS nie jest aż tak różna od wartości DFFITS naszego „wpływowego” punktu danych.

Przykład #4 (ponownie). Sprawdźmy różnicę w miarach dopasowania dla tego zestawu danych (influence4.txt):

Regresja y na x i zapytanie o różnicę w dopasowaniach, otrzymujemy następujące dane wyjściowe oprogramowania:

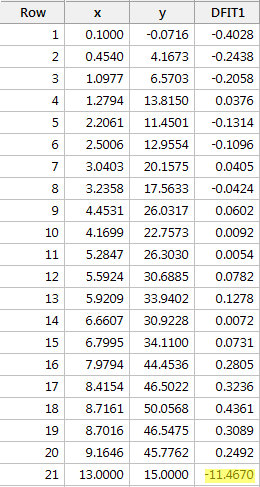
Używając obiektywnej wytycznej zdefiniowanej powyżej, ponownie uznajemy punkt danych za wpływowy, jeśli wartość bezwzględna jego wartości DFFITS jest większa niż:

Co o tym sądzisz? Czy któraś z wartości DFFITS wyróżnia się na tle innych? Errr – wartość DFFITS czerwonego punktu danych (-11.4670 ) jest z pewnością innej wielkości niż wszystkie pozostałe. W tym przypadku nie powinno być wątpliwości, że czerwony punkt danych jest wpływowy!

Odległość Cooka

Już wskakując tutaj, miara odległości Cooka, oznaczona Di, jest zdefiniowana jako:

Wygląda to trochę niechlujnie, ale główną rzeczą do rozpoznania jest to, że Di Cooka zależy zarówno od reszt, ei (w pierwszym członie), jak i od dźwigni, hii (w drugim członie). Oznacza to, że zarówno wartość x, jak i wartość y punktu danych odgrywają rolę w obliczaniu odległości Cooka.

W skrócie:

• Di bezpośrednio podsumowuje, jak bardzo zmieniają się wszystkie dopasowane wartości, gdy i-ta obserwacja zostanie usunięta.
• Punkt danych posiadający duże Di wskazuje, że punkt danych silnie wpływa na dopasowane wartości.

Zbadajmy, co dokładnie oznacza to pierwsze stwierdzenie w kontekście niektórych z naszych przykładów.

Przykład #1 (ponownie). Być może pamiętasz, że wykres tych danych (influence1.txt) sugeruje, że nie ma żadnych odstających ani wpływowych punktów danych dla tego przykładu:

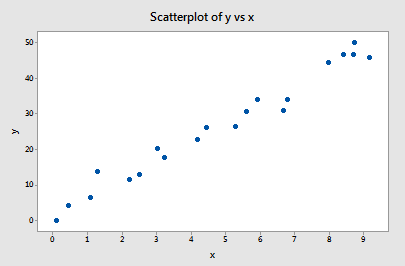
Jeśli regresujemy y na x używając wszystkich n = 20 punktów danych, ustalamy, że szacowany współczynnik przechyłu b0 = 1,732 i szacowany współczynnik nachylenia b1 = 5,117. Jeśli usuniemy pierwszy punkt danych z zestawu danych i dokonamy regresji y na x przy użyciu pozostałych n = 19 punktów danych, ustalimy, że szacowany współczynnik przechyłu b0 = 1,732 i szacowany współczynnik nachylenia b1 = 5,1169. Jak można się spodziewać, szacunki nie zmieniają się zbytnio po usunięciu jednego punktu danych. Kontynuując proces usuwania każdego punktu danych po kolei i wykreślając wynikające z tego szacunkowe nachylenia (b1) względem szacunkowych punktów przecięcia (b0), otrzymujemy:

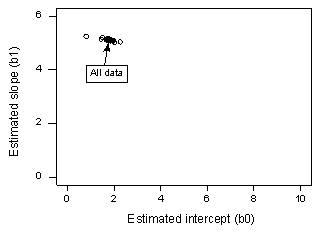
Solidny czarny punkt reprezentuje szacunkowe współczynniki oparte na wszystkich n = 20 punktach danych. Otwarte okręgi reprezentują każdy z szacowanych współczynników uzyskanych po usunięciu każdego punktu danych po kolei. Jak widać, wszystkie szacowane współczynniki są zgrupowane razem, niezależnie od tego, który, jeśli w ogóle, punkt danych został usunięty. Sugeruje to, że żaden punkt danych nie wpływa nadmiernie na szacowaną funkcję regresji lub, z kolei, na dopasowane wartości. W tym przypadku oczekiwalibyśmy, że wszystkie miary odległości Cooka, Di, będą małe.

Przykład #4 (ponownie). Być może pamiętasz, że wykres tych danych (influence4.txt) sugeruje, że jeden punkt danych jest wpływowy i odstający dla tego przykładu:

Jeśli regresujemy y na x przy użyciu wszystkich n = 21 punktów danych, ustalamy, że szacowany współczynnik przechyłu b0 = 8,51 i szacowany współczynnik nachylenia b1 = 3,32. Jeśli usuniemy czerwony punkt danych z zestawu danych i dokonamy regresji y na x przy użyciu pozostałych n = 20 punktów danych, ustalimy, że szacowany współczynnik przechyłu b0 = 1,732 oraz szacowany współczynnik nachylenia b1 = 5,1169. Oszacowania te zmieniają się znacząco po usunięciu jednego punktu danych. Kontynuując proces usuwania każdego punktu danych po kolei i wykreślając wynikające z tego szacunkowe nachylenia (b1) względem szacunkowych punktów przecięcia (b0), otrzymujemy:

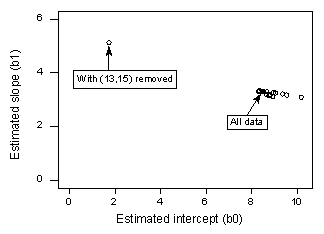
Ponownie, czarny punkt stały reprezentuje szacunkowe współczynniki oparte na wszystkich n = 21 punktach danych. Otwarte okręgi reprezentują każdy z szacowanych współczynników uzyskanych przy usuwaniu każdego punktu danych po kolei. Jak widać, z wyjątkiem czerwonego punktu danych (x = 13, y = 15), wszystkie szacowane współczynniki są zgrupowane razem, niezależnie od tego, który, jeśli w ogóle, punkt danych zostanie usunięty. Sugeruje to, że czerwony punkt danych jest jedynym punktem danych, który nadmiernie wpływa na szacowaną funkcję regresji i, z kolei, na dopasowane wartości. W tym przypadku oczekiwalibyśmy, że miara odległości Cook’a, Di, dla czerwonego punktu danych będzie duża, a miary odległości Cook’a, Di, dla pozostałych punktów danych będą małe.

Używanie miar odległości Cook’a. Piękno powyższych przykładów jest możliwość zobaczyć, co się dzieje z prostych działek. Niestety, nie możemy polegać na prostych działkach w przypadku regresji wielorakiej. Zamiast tego musimy polegać na wytycznych dotyczących podejmowania decyzji, kiedy miara odległości Cooka jest wystarczająco duża, aby uzasadnić traktowanie punktu danych jako wpływowego.

Oto wytyczne powszechnie stosowane:

• Jeśli Di jest większe niż 0,5, to i-ty punkt danych jest wart dalszego badania, ponieważ może być wpływowy.
• Jeśli Di jest większe niż 1, wtedy i-ty punkt danych jest całkiem prawdopodobne, że jest wpływowy.
• Lub, jeśli Di wystaje jak bolący kciuk z innych wartości Di, to prawie na pewno jest wpływowy.

Przykład #2 (ponownie). Sprawdźmy miarę odległości Cook’a dla tego zestawu danych (influence2.txt):

Regresja y na x i zapytanie o miary odległości Cooka, otrzymujemy następujące dane wyjściowe oprogramowania:

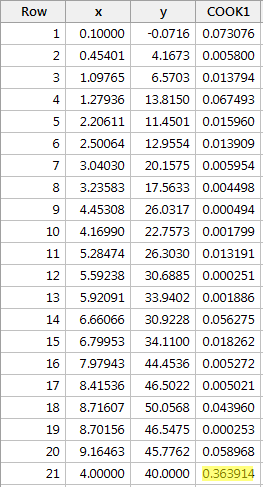
Miara odległości Cooka dla czerwonego punktu danych (0,363914) wyróżnia się nieco w porównaniu z innymi miarami odległości Cooka. Mimo to, miara odległości Cook’a dla czerwonego punktu danych jest mniejsza niż 0,5. Dlatego, w oparciu o miarę odległości Cooka, nie sklasyfikowalibyśmy czerwonego punktu danych jako wpływowego.

Przykład #3 (ponownie). Sprawdźmy miarę odległości Cook’a dla tego zestawu danych (influence3.txt):

Regresja y na x i zapytanie o miary odległości Cooka, otrzymujemy następujące dane wyjściowe oprogramowania:

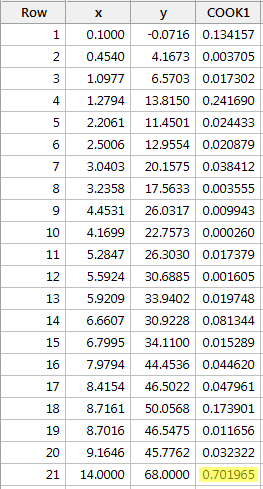
Miara odległości Cooka dla czerwonego punktu danych (0,701965) wyróżnia się nieco w porównaniu z innymi miarami odległości Cooka. Mimo to, miara odległości Cooka dla czerwonego punktu danych jest większa niż 0.5, ale mniejsza niż 1. Dlatego, bazując na miarze odległości Cooka, być może badalibyśmy dalej, ale niekoniecznie klasyfikowalibyśmy czerwony punkt danych jako wpływowy.

Przykład #4 (ponownie). Sprawdźmy miarę odległości Cooka dla tego zestawu danych (influence4.txt):

Regresja y na x i zapytanie o miary odległości Cooka, otrzymujemy następujące dane wyjściowe oprogramowania:

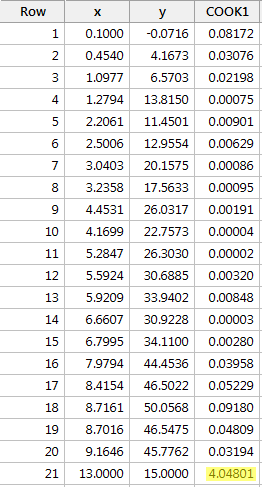
W tym przypadku, miara odległości Cooka dla czerwonego punktu danych (4.04801) wyróżnia się znacząco w porównaniu z innymi miarami odległości Cooka. Ponadto, miara odległości Cooka dla czerwonego punktu danych jest większa niż 1. Dlatego też, w oparciu o miarę odległości Cooka – i nie jest to zaskakujące – sklasyfikowalibyśmy czerwony punkt danych jako wpływowy.

Alternatywną metodą interpretacji odległości Cooka, która jest czasami używana, jest odniesienie miary do rozkładu F(k+1, n-k-1) i znalezienie odpowiadającej jej wartości percentyla. Jeśli ten percentyl jest mniejszy niż około 10 lub 20 procent, wtedy przypadek ma niewielki widoczny wpływ na dopasowane wartości. Z drugiej strony, jeśli jest on bliski 50 procent lub nawet wyższy, wtedy przypadek ma duży wpływ. (Cokolwiek „pomiędzy” jest bardziej niejednoznaczne.)

.