Łagodne wprowadzenie do problemu wypukłego kadłuba

Wypukłe kadłuby mają tendencję do bycia użytecznymi w wielu różnych dziedzinach, czasami dość nieoczekiwanie. W tym artykule wyjaśnię podstawowe Idea 2d wypukłych kadłubów i jak korzystać z graham scan, aby je znaleźć. Więc jeśli już wiesz o graham scan, to ten artykuł nie jest dla Ciebie, ale jeśli nie, to powinno zapoznać się z niektórymi z odpowiednich koncepcji.

The convex hull of a set of points is defined as the smallest convex polygon, that encloses all of the points in the set. Wypukły oznacza, że wielokąt nie ma żadnego kąta, który jest zagięty do wewnątrz.

Czerwone krawędzie na prawym wielokącie zamykają narożnik, w którym kształt jest wklęsły, czyli odwrotnie niż wypukły.

Przydatnym sposobem myślenia o kadłubie wypukłym jest analogia z gumką. Załóżmy, że punkty w zbiorze to gwoździe, wystające z płaskiej powierzchni. Wyobraźmy sobie teraz, co by się stało, gdybyśmy wzięli gumkę i rozciągnęli ją wokół gwoździ. Próbując powrócić do swojej pierwotnej długości, gumka otoczyłaby gwoździe, dotykając tych, które wystają najdalej od środka.

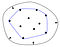
Aby reprezentować wynikowy wypukły kadłub w kodzie, zwykle przechowujemy listę punktów, które utrzymują tę gumkę, tj. listę punktów na wypukłym kadłubie.

Zauważ, że nadal musimy zdefiniować, co powinno się stać, jeśli trzy punkty leżą na tej samej linii. Jeśli wyobrazimy sobie, że gumka ma punkt, w którym dotyka jednego z gwoździ, ale wcale się tam nie zgina, to znaczy, że gwóźdź w tym miejscu leży na linii prostej między dwoma innymi gwoździami. W zależności od problemu, możemy uznać, że ten gwóźdź wzdłuż linii prostej jest częścią wyjścia, ponieważ dotyka gumki. Z drugiej strony, możemy też powiedzieć, że ten gwóźdź nie powinien być częścią wyjścia, ponieważ kształt gumki nie zmienia się, gdy ją usuwamy. Ta decyzja zależy od problemu, nad którym aktualnie pracujemy, a najlepiej, jeśli mamy dane wejściowe, w których żadne trzy punkty nie są współliniowe (tak jest często w łatwych zadaniach na konkursy programistyczne), wtedy możemy nawet całkowicie zignorować ten problem.

Znajdowanie kadłuba wypukłego

Patrząc na zbiór punktów, ludzka intuicja pozwala nam szybko zorientować się, które punkty prawdopodobnie będą dotykać kadłuba wypukłego, a które będą bliżej środka, a tym samym z dala od kadłuba wypukłego. Ale przełożenie tej intuicji na kod wymaga trochę pracy.

Aby znaleźć wypukły kadłub zbioru punktów, możemy użyć algorytmu zwanego skanowaniem Grahama, który jest uważany za jeden z pierwszych algorytmów geometrii obliczeniowej. Używając tego algorytmu, możemy znaleźć podzbiór punktów, które leżą na wypukłym kadłubie, wraz z kolejnością, w jakiej te punkty są napotykane podczas obchodzenia wypukłego kadłuba.

Algorytm rozpoczyna się od znalezienia punktu, o którym wiemy, że na pewno leży na wypukłym kadłubie. Za bezpieczny wybór można uznać np. punkt o najmniejszej współrzędnej y. Jeśli istnieje wiele punktów na tej samej współrzędnej y, bierzemy ten, który ma największą współrzędną x (działa to również z innymi punktami narożnymi, np. najpierw najniższy x, potem najniższy y).

Następnie sortujemy pozostałe punkty według kąta, pod jakim leżą w stosunku do punktu początkowego. Jeśli dwa punkty leżą pod tym samym kątem, to punkt, który jest bliżej punktu początkowego, powinien wystąpić wcześniej w sortowaniu.

Teraz ideą algorytmu jest chodzenie po tej posortowanej tablicy, określając dla każdego punktu, czy leży on na kadłubie wypukłym, czy nie. Oznacza to, że dla każdej trójki punktów, które napotkamy, decydujemy czy tworzą one narożnik wypukły czy wklęsły. Jeśli narożnik jest wklęsły, to wiemy, że środkowy punkt z tego tripletu nie może leżeć na kadłubie wypukłym.

(Zauważ, że terminy wklęsły i wypukły narożnik muszą być używane w odniesieniu do całego wielokąta, po prostu narożnik sam w sobie nie może być ani wypukły, ani wklęsły, ponieważ nie byłoby kierunku odniesienia.)

Przechowujemy punkty, które leżą na wypukłym kadłubie na stosie, w ten sposób możemy dodać punkty, jeśli dotrzemy do nich na naszej drodze wokół posortowanych punktów, i usunąć je, jeśli okaże się, że tworzą wklęsły narożnik.

(Ściśle mówiąc, musimy mieć dostęp do dwóch górnych punktów stosu, dlatego używamy zamiast tego std::vector, ale myślimy o tym jako o rodzaju stosu, ponieważ zawsze jesteśmy zainteresowani tylko kilkoma górnymi elementami.)

Przechodząc wokół posortowanej tablicy punktów, dodajemy punkt do stosu, a jeśli później stwierdzimy, że punkt nie należy do kadłuba wypukłego, usuwamy go.

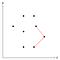
Możemy zmierzyć, czy bieżący narożnik zagina się do wewnątrz czy na zewnątrz, obliczając iloczyn krzyżowy i sprawdzając, czy jest on dodatni czy ujemny. Na rysunku powyżej widać trójkę punktów, w której tworzony przez nie narożnik jest wypukły, dlatego środkowy z tych trzech punktów pozostaje na razie na stosie.

Przechodząc do kolejnego punktu, robimy to samo: sprawdzamy, czy narożnik jest wypukły, a jeśli nie, usuwamy punkt. Następnie przechodzimy do dodawania kolejnego punktu i powtarzamy.

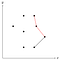
Ten narożnik zaznaczony na czerwono jest wklęsły, dlatego usuwamy środkowy punkt ze stosu, ponieważ nie może on być częścią kadłuba wypukłego.

Skąd wiemy, że to da nam poprawną odpowiedź?

Pisanie rygorystycznego dowodu jest poza zakresem tego artykułu, ale mogę zapisać podstawowe idee. Zachęcam Cię jednak do dalszej pracy i próby uzupełnienia luk!

Ponieważ obliczyliśmy iloczyn krzyżowy w każdym rogu, wiemy na pewno, że otrzymamy wielokąt wypukły. Teraz musimy tylko udowodnić, że ten wielokąt wypukły naprawdę zawiera wszystkie punkty.

(Właściwie trzeba by też pokazać, że jest to najmniejszy możliwy wielokąt wypukły spełniający te warunki, ale to wynika dość łatwo z tego, że punkty narożne naszego wielokąta wypukłego są podzbiorem pierwotnego zbioru punktów.)

Załóżmy, że istnieje punkt P leżący poza wielokątem, który właśnie znaleźliśmy.

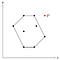
Ponieważ każdy punkt został raz dodany na stos, wiemy, że P został w pewnym momencie zdjęty ze stosu. Oznacza to, że P wraz z sąsiednimi punktami, nazwijmy je O i Q, utworzył wklęsły narożnik.

Ponieważ O i Q leżą wewnątrz wielokąta (lub na jego granicy), P musiałby również leżeć wewnątrz granicy, bo wielokąt jest wypukły, a narożnik, który O i Q tworzą z P, jest wklęsły względem wielokąta.

Znaleźliśmy więc sprzeczność, co oznacza, że taki punkt P nie może istnieć.

Implementacja

Dostarczona tutaj implementacja posiada funkcję convex_hull, która pobiera std::vector, która zawiera punkty jako std::pairs of ints i zwraca inną std::vector, która zawiera punkty, które leżą na wypukłym kadłubie.

Analiza czasu pracy i pamięci

Zawsze warto myśleć o algorytmach złożoności w kategoriach notacji Big-O, której nie będę tutaj wyjaśniał, ponieważ Michael Olorunnisola tutaj już wykonał znacznie lepszą pracę wyjaśniając ją niż ja prawdopodobnie:

Sortowanie punktów początkowo zajmuje O(n log n) czas, ale po tym, każdy krok może być obliczony w stałym czasie. Każdy punkt jest dodawany i usuwany ze stosu co najwyżej raz, co oznacza, że najgorszy czas działania leży w O(n log n).

Zużycie pamięci, które leży w O(n) w tej chwili, może być zoptymalizowane przez usunięcie potrzeby stosowania stosu i wykonywanie operacji bezpośrednio na tablicy wejściowej. Moglibyśmy przenieść punkty leżące na wypukłym kadłubie na początek tablicy wejściowej i ułożyć je w odpowiedniej kolejności, a pozostałe punkty zostałyby przeniesione do reszty tablicy. Funkcja mogłaby wtedy zwracać tylko jedną zmienną całkowitą, oznaczającą ilość punktów w tablicy, które leżą na kadłubie wypukłym. To oczywiście ma tę wadę, że funkcja staje się o wiele bardziej skomplikowana, dlatego odradzam ją, chyba że kodujesz dla systemów wbudowanych lub masz podobnie restrykcyjne obawy dotyczące pamięci. Dla większości sytuacji, kompromis prawdopodobieństwo błędu / oszczędność pamięci jest po prostu nie warto.

Inne algorytmy

Alternatywą dla skanowania Grahama jest algorytm Chana, który jest oparty na tym samym pomyśle, ale jest łatwiejszy do wdrożenia. Warto jednak najpierw zrozumieć, jak działa Graham Scan.

Jeśli naprawdę masz ochotę i chcesz zmierzyć się z problemem w trzech wymiarach, spójrz na algorytm Preparata i Honga wprowadzony w ich pracy z 1977 roku „Convex Hulls of Finite Sets of Points in Two and Three Dimensions”.

.