Wat is analytische meetkunde?

Analytische meetkunde is een tak van de algebra die wordt gebruikt om meetkundige objecten te modelleren – punten, (rechte) lijnen en cirkels zijn hiervan de meest basale. Analytische meetkunde is een grote uitvinding van Descartes en Fermat.

In de vlakke analytische meetkunde worden punten gedefinieerd als geordende paren van getallen, zeg, (x, y), terwijl de rechte lijnen op hun beurt worden gedefinieerd als de verzamelingen van punten die voldoen aan lineaire vergelijkingen, zie de uitstekende uiteenzettingen van D. Pedoe of D. Brannan e.a. Vanuit het gezichtspunt van de analytische meetkunde zijn meetkundige axioma’s afleidbare stellingen. Bijvoorbeeld, voor twee verschillende punten (x1, y1) en (x2, y2) is er één enkele rechte ax + by + c = 0 die door deze punten gaat. De coëfficiënten a, b, c kunnen (tot op een constante factor) gevonden worden uit het lineair stelsel van twee vergelijkingen

of rechtstreeks uit de determinantvergelijking

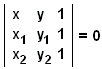Hoewel geen enkele axiomatische theorie kan ontsnappen aan het gebruik van ongedefinieerde elementen. In de verzamelingenleer, die ten grondslag ligt aan een groot deel van de wiskunde en in het bijzonder aan de analytische meetkunde, blijft het meest fundamentele begrip verzameling ongedefinieerd.

De meetkunde van de driedimensionale ruimte wordt gemodelleerd met drievoudige getallen (x, y, z) en een 3D lineaire vergelijking ax + by + cz + d = 0 definieert een vlak. In het algemeen is de analytische meetkunde een handig hulpmiddel om in hogere dimensies te werken.

In het kader van de analytische meetkunde kan men ook niet-Euclidische meetkunde modelleren (en doet men dat ook). In de vlakke projectieve meetkunde bijvoorbeeld is een punt een drietal homogene coördinaten (x, y, z), niet alle 0, zodanig dat

voor alle t ≠ 0, terwijl een rechte beschreven wordt door een homogene vergelijking

In de analytische meetkunde worden kegelsneden gedefinieerd door tweedegraadsvergelijkingen:

Dat deel van de analytische meetkunde dat zich vooral met lineaire vergelijkingen bezighoudt, heet Lineaire Algebra.

Cartesische analytische meetkunde is meetkunde waarbij de assen x = 0 en y = 0 loodrecht op elkaar staan.

De componenten van het n-getal x = (x1, …, xn) heten de coördinaten. Wanneer n = 2 of n = 3, wordt de eerste coördinaat abscis genoemd en de tweede ordinaat.

1. D. A. Brannan, M. F. Esplen, J. J. Gray, Geometry, Cambridge University Press, 2002
2. D. Pedoe, Geometry: A Comprehensive Course, Dover, 1988

|Contact||Voorpagina||Inhoud||Geometrie||Up|

Copyright © 1996-2018 Alexander Bogomolny