Mathematics for the Liberal Arts

Naast visuele zelfgelijkvormigheid, vertonen fractals nog andere interessante eigenschappen. Merk bijvoorbeeld op dat elke stap van de Sierpinski pakking iteratie een kwart van het resterende gebied verwijdert. Als dit proces tot in het oneindige wordt voortgezet, zouden we uiteindelijk in wezen al het gebied verwijderen, wat betekent dat we begonnen met een 2-dimensionaal gebied, en op de een of andere manier eindigen met iets minder dan dat, maar schijnbaar meer dan slechts een 1-dimensionale lijn.

Om dit idee te onderzoeken, moeten we de dimensie bespreken. Zoiets als een lijn is eendimensionaal; hij heeft alleen lengte. Elke kromme is 1-dimensionaal. Dingen als dozen en cirkels zijn 2-dimensionaal, omdat ze lengte en breedte hebben, waarmee een oppervlakte wordt beschreven. Voorwerpen zoals dozen en cilinders hebben lengte, breedte en hoogte, wat een volume beschrijft, en zijn 3-dimensionaal.

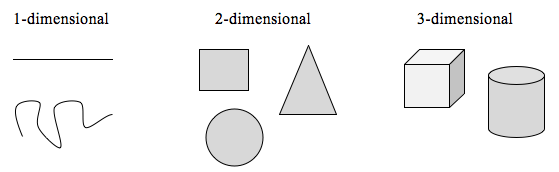
Er gelden bepaalde regels voor het schalen van objecten, gerelateerd aan hun dimensie.

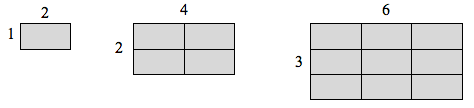
Als ik een lijn met lengte 1 had, en ik wilde de lengte daarvan met 2 schalen, dan zou ik twee kopieën van de oorspronkelijke lijn nodig hebben. Als ik een lijn met lengte 1 had, en de lengte daarvan met 3 wilde schalen, zou ik drie kopieën van het origineel nodig hebben.

Als ik een rechthoek had met lengte 2 en hoogte 1, en ik wilde de lengte en breedte ervan met 2 schalen, dan had ik vier kopieën van de oorspronkelijke rechthoek nodig. Als ik de lengte en breedte met 3 wil schalen, heb ik negen kopieën van de oorspronkelijke rechthoek nodig.

Als ik een kubusvormige doos had met zijden van lengte 1, en ik wilde de lengte en breedte daarvan met 2 schalen, dan had ik acht kopieën nodig van de oorspronkelijke kubus. Als ik de lengte en breedte met 3 wil schalen, heb ik 27 kopieën van de oorspronkelijke kubus nodig.

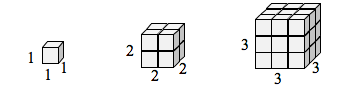
Merk op dat in het eendimensionale geval, de benodigde kopieën = schaal.

In het tweedimensionale geval, de benodigde kopieën = schaal^{2}.

In het driedimensionale geval, de benodigde kopieën = schaal^{3}.

Uit deze voorbeelden kunnen we een patroon afleiden.

Voorbeeld

Gebruik de schaal-dimensie relatie om de dimensie van de Sierpinski pakking te bepalen.

Voorstel dat we de oorspronkelijke pakking definiëren als met zijde 1. De grotere afgebeelde pakking is twee keer zo breed en twee keer zo hoog, dus geschaald met een factor 2.

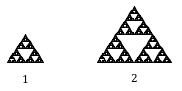
Merk op dat voor de constructie van de grotere pakking 3 kopieën van de originele pakking nodig zijn.

Gebruik makend van de schaal-dimensie relatie C=S^{D}, krijgen we de vergelijking 3=2^{D}.

Sinds 2^{1}=2 en 2^{2}=4, zien we onmiddellijk dat D ergens tussen 1 en 2 ligt; de pakking is meer dan een eendimensionale vorm, maar we hebben zoveel oppervlakte weggenomen dat hij nu minder dan tweedimensionaal is.

Voor het oplossen van de vergelijking 3=2^{D} zijn logaritmen nodig. Als je eerder logaritmen hebt bestudeerd, weet je misschien nog hoe je deze vergelijking oplost (zo niet, ga dan naar het vakje hieronder en gebruik die formule met de logtoets op een rekenmachine):

Neem de logaritme van beide zijden.

3={{2}^{D}}

Gebruik de exponent eigenschap van logs.

Log(3)=({{2}^{D}})rechts)

Deel door log(2).

D=log(3)=Dlog(2)

De afmeting van de pakking is ongeveer 1.585.

D={log(3)}{log(2)}

D=1.585.

D={log(3)}{\log(2)}

D=1.585.

585

Probeer het

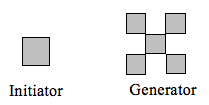
Bepaal de fractale dimensie van de fractal die met de initiator en generator gemaakt is.

Oplossing tonen

Om de fractal met een factor 3 te schalen zijn 5 kopieën van het origineel nodig.

D=D=0,465

In de volgende video laten we aan de hand van een uitgewerkt voorbeeld zien hoe je de dimensie van de Sierpinski pakking kunt bepalen