Introducing Consistent Hashing

Met de opkomst van gedistribueerde architecturen, werd consistent hashing mainstream. Maar wat is het precies en hoe verschilt het van een standaard hashing-algoritme? Wat zijn de precieze beweegredenen erachter?
Eerst zullen we de belangrijkste concepten beschrijven. Daarna zullen we in bestaande algoritmen duiken om de uitdagingen van consistent hashen te begrijpen.
Hashing
Hashing is het proces om gegevens van willekeurige grootte om te zetten in waarden van vaste grootte. Elk bestaand algoritme heeft zijn eigen specificatie:
- MD5 produceert 128-bit hash-waarden.
- SHA-1 produceert 160-bit hash-waarden.
- enz.
Hashing kent vele toepassingen in de informatica. Een van deze toepassingen heet bijvoorbeeld checksum. Om de integriteit van een dataset te verifiëren, kan een hashing-algoritme worden gebruikt. Een server hasht een dataset en geeft de hash-waarde door aan een client. Vervolgens hasht de client zijn versie van de dataset en vergelijkt de hash-waarden. Als ze gelijk zijn, moet de integriteit worden geverifieerd.
De “moeten” hier is belangrijk. Het slechtst denkbare scenario is als er een botsing optreedt. Een botsing is wanneer twee verschillende stukken gegevens dezelfde hash-waarde hebben. Laten we een voorbeeld uit het echte leven nemen door de volgende hashing functie te definiëren: gegeven aan een persoon geeft het zijn geboortedatum terug (dag & geboortemaand). De verjaardagsparadox vertelt ons dat als we maar 23 mensen in een kamer hebben, de kans dat twee personen dezelfde verjaardag hebben (dus een botsing) meer dan 50% is. Daarom is de verjaardagsfunctie waarschijnlijk geen goede hashing functie.

Als een snelle inleiding op hashing is het belangrijk om te begrijpen dat het hoofdidee gaat over het verspreiden van waarden over een domein. Bijvoorbeeld:
- MD5 verspreidt waarden over een 128-bit ruimtedomein
- Een hashtable (of hashmap) met een array van 32 elementen heeft een interne hashing-functie die waarden verspreidt naar elke index (van 0 tot 31).
Load Distribution
Load distribution kan worden gedefinieerd als het proces van het verspreiden van belasting over nodes. De term node is hier uitwisselbaar met server of instance. Het is een rekeneenheid.
Load balancing is een voorbeeld van load distribution. Het gaat om het verdelen van een set taken over een set bronnen. We gebruiken bijvoorbeeld load balancing om de API-verzoeken te verdelen over webserver-instanties.
Wanneer het om gegevens gaat, gebruiken we liever de term sharding. Een database shard is een horizontale partitie van gegevens in een database. Een typisch voorbeeld is een database gepartitioneerd in drie shards waarbij elke shard een subset van de totale data heeft.
Load balancing en sharding hebben een aantal gemeenschappelijke uitdagingen. Het gelijkmatig verdelen van gegevens bijvoorbeeld om te garanderen dat een knooppunt niet wordt overbelast in vergelijking met de andere. In sommige contexten moeten load balancing en sharding ook taken of gegevens aan dezelfde node koppelen:
- Als we de operaties voor een bepaalde consument moeten serialiseren, één voor één afhandelen, moeten we het verzoek naar dezelfde node routeren.
- Als we gegevens moeten distribueren, moeten we weten welke shard de eigenaar is voor een bepaalde key.
Klinkt dat bekend? In deze twee voorbeelden, verspreiden we waarden over een domein. Of het nu een taak is die verspreid wordt over server nodes of gegevens die verspreid worden over database shard, we vinden het idee terug dat geassocieerd wordt met hashing. Dit is de reden waarom hashing kan worden gebruikt in combinatie met lastverdeling. Laten we eens kijken hoe.
Mod-n Hashing
Het principe van mod-n hashing is het volgende. Elke sleutel wordt gehasht met een hashing-functie om een invoer in een geheel getal om te zetten. Daarna voeren we een modulo uit gebaseerd op het aantal nodes.
Laten we eens een concreet voorbeeld met 3 nodes bekijken. Hier moeten we de belasting verdelen over deze knooppunten op basis van een sleutelidentificatie. Elke sleutel wordt gehashed en dan voeren we een modulo operatie uit:

Het voordeel van deze aanpak is zijn stateloosheid. We hoeven geen status bij te houden om ons eraan te herinneren dat foo naar knooppunt 2 is gerouteerd. Toch moeten we weten hoeveel nodes geconfigureerd zijn om de modulo operatie toe te passen.
Dan, hoe werkt het mechanisme in het geval van scaling out of in (toevoegen of verwijderen van nodes)? Als we nog een node toevoegen, is de modulo operatie nu gebaseerd op 4 in plaats van 3:

Zoals we kunnen zien, zijn de sleutels foo en baz niet meer geassocieerd met dezelfde node. Met mod-n hashing, is er geen garantie om enige consistentie te behouden in de sleutel/knooppunt associatie. Is dit een probleem? Dat zou kunnen.
Wat als we een datastore implementeren die gebruik maakt van sharding en gebaseerd is op de mod-n strategie om data te distribueren? Als we het aantal nodes schalen, moeten we een herbalanceringsoperatie uitvoeren. In het vorige voorbeeld betekent rebalancing:
-
fooverplaatsen van node 2 naar node 0. -
bazverplaatsen van node 2 naar node 3.
Nu, wat gebeurt er als we miljoenen of zelfs miljarden gegevens hadden opgeslagen en dat we bijna alles opnieuw in balans moeten brengen? Zoals we ons kunnen voorstellen, zou dit een zwaar proces zijn. Daarom moeten we onze belastingverdelingstechniek veranderen om ervoor te zorgen dat bij het herbalanceren:
- De verdeling zo uniform mogelijk blijft op basis van het nieuwe aantal nodes.
- Het aantal sleutels dat we moeten migreren, moet beperkt zijn. Idealiter zou het slechts 1/n procent van de sleutels zijn, waarbij n het aantal nodes is.
Dit is precies het doel van consistente hashing-algoritmen.
De term consistent kan echter enigszins verwarrend zijn. Ik heb ingenieurs ontmoet die ervan uitgingen dat dergelijke algoritmen een bepaalde sleutel aan hetzelfde knooppunt bleven koppelen, zelfs in het licht van schaalbaarheid. Dit is niet het geval. Het moet consistent zijn tot een bepaald punt om de verdeling uniform te houden.
Nu is het tijd om in enkele oplossingen te graven.
Rendezvous
Rendezvous was het eerste algoritme dat ooit werd voorgesteld om ons probleem op te lossen. Hoewel in de oorspronkelijke studie, gepubliceerd in 1996, de term consistent hashing niet wordt genoemd, biedt het wel een oplossing voor de uitdagingen die we beschreven. Laten we eens kijken naar een mogelijke implementatie in Go:
Hoe werkt het? We gaan door elke node en berekenen de hash-waarde. De hashwaarde wordt geretourneerd door een hash-functie die een geheel getal produceert op basis van een sleutel (onze invoer) en een knooppuntidentificatiesymbool (de eenvoudigste aanpak is om de aaneenschakeling van de twee strings te hashen). Vervolgens geven we het knooppunt met de hoogste hash-waarde terug. Dit is de reden waarom het algoritme ook bekend staat als highest random weight hashing.
Het grootste nadeel van rendezvous is zijn O(n) tijd complexiteit waarbij n het aantal nodes is. Het is zeer efficiënt als we een beperkt aantal nodes nodig hebben. Maar als we duizenden nodes gaan onderhouden, kan het prestatieproblemen gaan opleveren.
Ring Consistent Hash
Het volgende algoritme werd in 1997 uitgebracht door Karger et al. in dit paper. Deze studie noemde voor het eerst de term consistent hashing.
Het is gebaseerd op een ring (een end-to-end verbonden array). Hoewel het het populairste consistente hashing-algoritme is (of in ieder geval het bekendste), wordt het principe niet altijd goed begrepen. Laten we er eens in duiken.
De eerste operatie is het maken van de ring. Een ring heeft een vaste lengte. In ons voorbeeld verdelen we hem in 12 delen:

Dan positioneren we onze nodes. In ons voorbeeld zullen we N0, N1 en N2 definiëren.
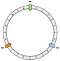
De nodes worden voorlopig gelijkmatig verdeeld. We komen hier later nog op terug.
Dan wordt het tijd om te kijken hoe we de sleutels gaan representeren. Eerst hebben we een functie f nodig die een ring index (van 0 tot 11) teruggeeft op basis van een sleutel. We kunnen daarvoor mod-n hashing gebruiken. Aangezien de lengte van de ring constant is, zal dat geen probleem opleveren.
In ons voorbeeld zullen we 3 sleutels definiëren: a, b en c. We passen f toe op elke sleutel. Laten we aannemen dat we de volgende resultaten hebben:
f(a) = 1f(a) = 5f(a) = 7
Daarom kunnen we de toetsen op de ring op deze manier plaatsen:
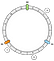
Hoe koppelen we een bepaalde sleutel aan een knooppunt? De belangrijkste logica is om vooruit te gaan. Van een gegeven sleutel geven we het eerste knooppunt terug dat we vinden terwijl we voorwaarts gaan:

In dit voorbeeld associëren we a met N1, b en c met N2.
Nu gaan we eens kijken hoe het opnieuw in evenwicht brengen wordt beheerd. We definiëren een ander knooppunt N3. Waar moeten we die plaatsen? Er is geen ruimte meer om de totale verdeling uniform te maken. Moeten we de knooppunten herschikken? Nee, anders zouden we niet meer consistent zijn, is het niet? Om een node te positioneren hergebruiken we dezelfde hashing functie f die we introduceerden. In plaats van te worden aangeroepen met een sleutel, kan hij worden aangeroepen met een knooppunt-identifier. Dus de positie van het nieuwe knooppunt wordt willekeurig bepaald.
Een vraag rijst dan: wat moeten we doen met a aangezien het volgende knooppunt niet meer N1 is:

De oplossing is de volgende: we moeten de associatie veranderen en a laten associëren met N3:

Zoals we eerder hebben besproken, zou een ideaal algoritme gemiddeld 1/n procent van de sleutels opnieuw in evenwicht moeten brengen. In ons voorbeeld, nu we een vierde node toevoegen, zouden we 25% van de mogelijke sleutels moeten herkoppelen aan N3. Is dit het geval?
-
N0van indices 8 tot 12: 33.3% van het totaal aantal sleutels -
N1van indices 2 tot 4: 16.6% van het totaal aantal sleutels -
N2van indices 4 tot 8: 33.3% van het totaal aantal sleutels -
N3van de indexen 0 tot en met 2: 16,6% van het totaal aantal sleutels
De verdeling is niet uniform. Hoe kunnen we dat verbeteren? De oplossing is het gebruik van virtuele nodes.
Laten we zeggen dat we in plaats van een enkele spot per node, er drie kunnen plaatsen. Ook moeten we drie verschillende hashing functies definiëren. Elk knooppunt wordt drie keer gehasht, zodat we drie verschillende indices krijgen:
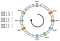
We kunnen hetzelfde algoritme toepassen door vooruit te bewegen. Toch zou een sleutel worden geassocieerd met een knooppunt, ongeacht het virtuele knooppunt dat het ontmoette.
In dit voorbeeld zou de verdeling nu als volgt zijn:
-
N0: 33,3% -
N1: 25% -
N2: 41,6%
Hoe meer virtuele knooppunten we per knooppunt definiëren, hoe meer de verdeling uniform zou moeten zijn. Gemiddeld, met 100 virtuele nodes per server, is de standaard verdeling ongeveer 10%. Met 1000 is dat ongeveer 3,2%.
Dit mechanisme is ook nuttig als we nodes hebben met verschillende afmetingen. Als een node bijvoorbeeld is geconfigureerd om theoretisch twee keer zoveel belasting aan te kunnen dan de anderen, kunnen we twee keer zoveel virtuele nodes draaien.
Het grootste nadeel van de virtuele nodes is echter de geheugenafdruk.
Voordat we verder gaan, is het interessant om op te merken dat een algoritme soms aanzienlijk kan worden verbeterd door een klein onderdeel te veranderen. Dit is bijvoorbeeld het geval met een algoritme dat in 2017 door Google is gepubliceerd, genaamd consistent hashing with bounded loads. Deze versie is gebaseerd op hetzelfde ring-idee dat we beschreven. Maar hun aanpak is om een kleine herbalancering uit te voeren bij elke update (een nieuwe sleutel of node toegevoegd/verwijderd). Deze versie doet het beter dan het origineel in termen van standaardafwijking, met als nadeel een slechtere tijdcomplexiteit.
Jump Consistent Hash
In 2007 publiceerden twee ingenieurs van Google jump consistent hash. Vergeleken met het ring-gebaseerde algoritme, vereist deze implementatie “geen opslag, is sneller en doet beter werk in het gelijk verdelen van de sleutelruimte over de emmers en in het gelijk verdelen van de werklast wanneer het aantal emmers verandert”. Anders gezegd, het verbetert de verdeling van de werklast over de nodes (een bucket is hetzelfde begrip als een node) zonder enige geheugenoverhead.
Hier is het algoritme in C++ (7 regels code 🤯):
In ring consistent hash, met 1000 virtuele nodes was de standaardafwijking ongeveer 3,2%. Bij sprongconsistente hash hebben we het concept van virtuele knooppunten niet meer nodig. Toch blijft de standaardafwijking minder dan 0.0000001%.
Er is echter één beperking. De nodes moeten opeenvolgend genummerd zijn. Als we een lijst met servers foo, bar en baz hebben, kunnen we bar bijvoorbeeld niet verwijderen. Maar als we een data store configureren, kunnen we het algoritme toepassen om de shard index te krijgen op basis van het totaal aantal shards. Daarom kan jump consistent hash nuttig zijn in de context van sharding, maar niet load balancing.
Wat is het Perfect Consistent Hashing Algoritme?
Nadat we nu enige ervaring hebben met consistent hashing, laten we een stap terug doen en kijken wat het perfecte algoritme zou zijn:
- Nauwelijks 1/n procent van de sleutels zou gemiddeld worden geremapped, waarbij n het aantal nodes is.
- Een O(n) ruimtecomplexiteit waarbij n het aantal nodes is.
- Een O(1) tijdcomplexiteit per invoeging/verwijdering van een node en per sleutelopzoeking.
- Een minimale standaardafwijking om ervoor te zorgen dat een node niet overbelast is in vergelijking met een andere.
- Het zou mogelijk maken een gewicht aan een node te koppelen om met verschillende node sizing om te gaan.
- Het zou willekeurige noden namen toestaan (niet opeenvolgend genummerd) om zowel load balancing als sharding te ondersteunen.
Gelukkig genoeg bestaat dit algoritme niet. Gebaseerd op wat we zagen:
- Rendezvous heeft een lineaire tijd complexiteit per lookup.
- Ring consistente hash heeft een slechte minimale standaardafwijking zonder het concept van virtuele nodes. Met virtuele nodes is de ruimtecomplexiteit O(n*v) met n het aantal nodes en v het aantal virtuele nodes per node.
- Jump consistente hash heeft geen constante tijd complexiteit en het ondersteunt geen arbitraire nodes name.
Het onderwerp is nog steeds open en er zijn recente studies die de moeite waard zijn om te bekijken. Bijvoorbeeld, de multi-probe consistente hash uitgebracht in 2005. Het ondersteunt O(1) ruimte complexiteit. Maar om een standaardafwijking van ε te bereiken, vereist het O(1/ε) tijd per lookup. Als we bijvoorbeeld een standaardafwijking van minder dan 0,5% willen bereiken, moet de sleutel ongeveer 20 keer worden gehasht. We kunnen dus een minimale standaardafwijking krijgen, maar met een hogere opzoektijd.

Zoals we in de inleiding al zeiden, zijn consistente hashing-algoritmen mainstream geworden. Het wordt nu gebruikt in talloze systemen zoals MongoDB, Cassandra, Riak, Akka, enz., zij het in de context van het balanceren van belasting of het distribueren van gegevens. Maar, zoals zo vaak in de informatica, elke oplossing heeft tradeoffs.
Over tradeoffs gesproken, als je een follow-up nodig hebt, wil je misschien een kijkje nemen naar de uitstekende post geschreven door Damian Gryski:
Leave a Reply