Inleiding tot deconvolutie

Deconvolutie is een rekenintensieve beeldverwerkingstechniek die steeds meer wordt gebruikt voor het verbeteren van het contrast en de resolutie van digitale beelden die zijn vastgelegd in de microscoop. De fundamenten zijn gebaseerd op een reeks methoden die zijn ontworpen om de onscherpte die aanwezig is in microscoopbeelden en die wordt veroorzaakt door de beperkte opening van het objectief, te verwijderen of om te keren.

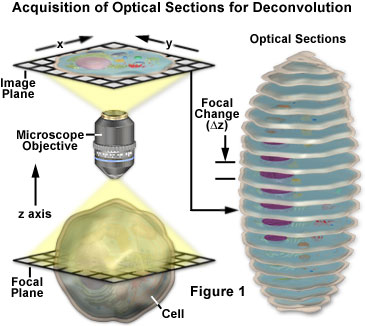
Nagenoeg elk beeld dat is opgenomen met een digitale fluorescentiemicroscoop kan worden gedeconvolueerd, en er worden verschillende nieuwe toepassingen ontwikkeld die deconvolutie-technieken toepassen op doorvallende lichtbeelden die zijn verzameld onder een verscheidenheid van contrastverhogende strategieën. Onder de meest geschikte onderwerpen voor verbetering door deconvolutie zijn drie-dimensionale montages opgebouwd uit een reeks optische doorsneden.

De basisconcepten rond de verwerving van z-reeks beelden voor deconvolutie analyse worden gepresenteerd met een schematisch diagram in figuur 1. Een reeks beelden wordt opgenomen van het monster, elk iets verschoven van elkaar langs de z-as. Deze verandering van brandpuntsvlak resulteert in een enigszins verschillend beeld, met subtiele veranderingen door onscherp licht dat van boven en onder het huidige z-vlak komt. Tijdens de deconvolutie analyse, wordt de gehele z-reeks geanalyseerd om een duidelijker, hogere resolutie gegevensreeks te creëren die niet door out of focus fluorescentie wordt gecompliceerd.

Deconvolutie wordt vaak gesuggereerd als een goed alternatief voor de confocale microscoop, aangezien beide technieken ernaar streven om het effect van out of focus fluorescentie op uw uiteindelijke beeld te minimaliseren. Dit is niet helemaal waar, omdat beelden die zijn verkregen met een pinhole-opening in een confocale microscoop baat hebben bij deconvolutieverwerking. Confocale microscopie voorkomt dat onscherp licht wordt gedetecteerd door een pinhole-opening tussen het objectief en de detector te plaatsen, waardoor alleen onscherpe lichtstralen kunnen passeren. Breedveldmicroscopen daarentegen laten onscherp licht rechtstreeks door naar de detector. Deconvolutie wordt dan toegepast op de resulterende beelden om het onscherpe licht af te trekken of het terug te leiden naar de bron. Confocale microscopie is bijzonder geschikt voor het onderzoek van dikke specimens zoals embryo’s of weefsels, terwijl de verwerking van breedvelddeconvolutie een krachtig hulpmiddel is gebleken voor de beeldvorming van specimens waarvoor extreem lage lichtniveaus vereist zijn. Deze hulpmiddelen kunnen zelfs worden gecombineerd om de ruis te verminderen in beelden die met een confocale microscoop zijn verkregen. Echter, een meerderheid van de deconvolutie experimenten gerapporteerd in de literatuur van toepassing op beelden opgenomen op een standaard widefield fluorescentiemicroscoop.

Bronnen van Beeld Degradatie

Image degradatie cam worden onderverdeeld in vier onafhankelijke bronnen: ruis, verstrooiing, schittering, en onscherpte. In figuur 2 worden voorbeelden gegeven van het visuele effect van elk van deze bronnen op hetzelfde beeld.

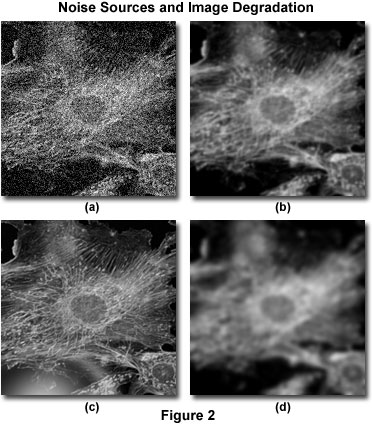
Ruis kan worden omschreven als een quasi-willekeurige ontregeling van details in een beeld, die (in zijn ernstigste vorm) het uiterlijk heeft van witte ruis of zout-en-paars-ruis, vergelijkbaar met wat men bij slechte ontvangst op televisie ziet (figuur 2(a)). Dit type ruis wordt “quasi-willekeurig” genoemd omdat de statistische verdeling kan worden voorspeld als de mechanica van de bron bekend is. In de digitale microscopie is de belangrijkste bron van ruis ofwel het signaal zelf (vaak “photon shot noise” genoemd), ofwel het digitale beeldvormingssysteem. De mechanica van beide ruisbronnen is bekend en derhalve is de statistische verdeling van de ruis bekend. Signaalafhankelijke ruis kan worden gekarakteriseerd door een Poisson-verdeling, terwijl ruis die afkomstig is van het beeldvormingssysteem vaak een Gaussiaanse verdeling volgt. Omdat de bron en de verdeling van gewone ruis in digitale beelden zo goed bekend zijn, kan zij gemakkelijk worden verwijderd door toepassing van de juiste beeldfilters, die gewoonlijk in de meeste deconvolutiesoftwarepakketten zijn opgenomen als een optionele “pre-processing”-routine.

Strooiing wordt gewoonlijk aangeduid als een willekeurige verstoring van licht, veroorzaakt door veranderingen in de brekingsindex in een specimen. Het netto-effect van verstrooiing is een werkelijk willekeurige disarrangement van beelddetails, zoals blijkt uit figuur 2(b). Hoewel geen volledig bevredigende methode is ontwikkeld om verstrooiing in een gegeven specimen te voorspellen, is aangetoond dat de mate van verstrooiing sterk afhankelijk is van de specimendikte en de optische eigenschappen van het specimen en de omringende inbeddingsmaterialen. De verstrooiing neemt toe met zowel de dikte van het specimen als met de heterogeniteit van de brekingsindex van de interne componenten binnen een specimen.

Gelijkaardig aan verstrooiing, is schittering een willekeurige verstoring van licht, maar komt voor in de optische elementen (lenzen, filters, prisma’s, enz.) van de microscoop in plaats van in het specimen. Het niveau van de schittering in een moderne microscoop is geminimaliseerd door het gebruik van lenzen en filters met antireflecterende coatings, en de verfijning van lensvormingstechnieken, optisch cement, en glasformules. Figuur 2(c) illustreert het effect van ongecontroleerde schittering.

Vaagheid wordt beschreven door een niet-willekeurige verspreiding van licht dat optreedt bij passage door het optische pad van het beeldvormingssysteem (figuur 2(d)). De belangrijkste bron van onscherpte is diffractie, en een beeld waarvan de resolutie alleen door onscherpte wordt beperkt, wordt geacht diffractiebegrensd te zijn. Dit is een intrinsieke limiet van elk beeldvormingssysteem en is de bepalende factor bij de beoordeling van de resolutielimiet van een optisch systeem. Gelukkig zijn er gesofisticeerde modellen van onscherpte in een optische microscoop beschikbaar die kunnen worden gebruikt om de bron van onscherpe fotonen te bepalen. Dit is de basis voor deconvolutie. Wegens het fundamentele belang ervan voor de deconvolutie, zal het theoretische model voor onscherpte in andere delen van dit hoofdstuk veel uitvoeriger worden besproken. Benadrukt moet echter worden dat alle beeldvormingssystemen onscherpte produceren, onafhankelijk van de andere vormen van beelddegradatie die door het specimen of de bijbehorende instrumentele elektronica worden veroorzaakt. Het is juist deze onafhankelijkheid van optische onscherpte van andere soorten degradatie die de mogelijkheid van onscherpteverwijdering door deconvolutietechnieken mogelijk maakt.

De interactie van licht met materie is de primaire fysische oorsprong van verstrooiing, verblinding en onscherpte. Echter, de samenstelling en rangschikking van moleculen in een bepaald materiaal (of het nu glas, water, of eiwit) verleent aan elk materiaal zijn eigen bijzondere reeks optische eigenschappen. In het kader van deconvolutie zijn de verschillen tussen verstrooiing, verblinding en onscherpte de plaats waar zij zich voordoen en de mogelijkheid om een mathematisch model voor deze verschijnselen op te stellen. Omdat verstrooiing een gelokaliseerd, onregelmatig verschijnsel is dat zich in het preparaat voordoet, is het moeilijk gebleken er een model van te maken. Omdat onscherpte daarentegen een functie is van het optische systeem van de microscoop (hoofdzakelijk het objectief), kan het met relatieve eenvoud worden gemodelleerd. Een dergelijk model maakt het mogelijk het onscherpheidsproces wiskundig om te keren, en deconvolutie gebruikt dit model om onscherpte om te keren of te verwijderen.

De Point Spread Function

Het model voor onscherpte dat zich in de theoretische optica heeft ontwikkeld, is gebaseerd op het concept van een driedimensionale point spread function (PSF). Dit concept is van fundamenteel belang voor deconvolutie en moet duidelijk worden begrepen om beeldartefacten te vermijden. De “point spread function” is gebaseerd op een oneindig kleine puntbron van licht afkomstig uit de ruimte van het specimen (object). Omdat het microscoopbeeldvormingssysteem slechts een fractie van het door dit punt uitgezonden licht opvangt, kan het licht niet worden gefocusseerd tot een perfect driedimensionaal beeld van het punt. In plaats daarvan lijkt het punt verbreed en verspreid in een driedimensionaal diffractiepatroon. De “point spread function” wordt dus formeel gedefinieerd als het driedimensionale diffractiepatroon dat wordt gegenereerd door een ideale puntlichtbron.

Afhankelijk van de gebruikte beeldvormingsmodus (breed veld, confocaal, doorvallend licht) heeft de “point spread function” een verschillende en unieke vorm en contour. Bij een breedveldfluorescentiemicroscoop lijkt de vorm van de “point spread function” op die van een langwerpige “voetbal” van licht, omgeven door een gloed van breder wordende ringen. Om de “point spread function” in drie dimensies te beschrijven, wordt gewoonlijk een coördinatenstelsel met drie assen (x, y en z) toegepast, waarbij × en y evenwijdig zijn met het brandvlak van het preparaat en z evenwijdig is met de optische as van de microscoop. In dit geval verschijnt de “point spread function” als een reeks concentrische ringen in het x-y vlak, en lijkt zij op een zandloper in het x-z en y-z vlak (zoals geïllustreerd in figuur 3). Een x-y doorsnede door het centrum van het brede veld point spread functie onthult een reeks concentrische ringen: de zogenaamde Airy schijf die vaak wordt genoemd in teksten over klassieke optische microscopie.

Twee x-z projecties van point spread functies met verschillende mate van sferische aberratie worden gepresenteerd in figuur 3. De optische as is evenwijdig aan de verticale as van het beeld. De puntspreidingsfunctie links vertoont een minimale sferische aberratie, terwijl die rechts een aanzienlijke mate van aberratie vertoont. Merk op dat de axiale asymmetrie en de verbreding van het centrale knooppunt langs de optische as in het rechter beeld leiden tot een verslechterde axiale resolutie en vervaging van het signaal. In theorie is de puntspreidingsfunctie oneindig groot en is de totale som van de lichtintensiteit in ver van het brandpunt verwijderde vlakken gelijk aan de som van de lichtintensiteiten in het brandpunt. De lichtintensiteit neemt echter snel af en wordt uiteindelijk niet meer te onderscheiden van ruis. In een niet-geabstraheerde puntspreidingsfunctie, opgenomen met een olie-immersie-objectief met hoge numerieke apertuur (1.40), wordt licht dat 0,2 vierkante micrometer inneemt op het scherpstelvlak, verspreid over 90 maal dat gebied op 1 micrometer boven en onder het scherpstelpunt. Het specimen dat gebruikt werd om deze beelden op te nemen was een fluorescerende kraal met een diameter van 0,1 micrometer, gemonteerd in glycerol (brekingsindex gelijk aan 1,47), met immersie-oliën met de brekingsindices zoals vermeld in de figuur.

Een belangrijke overweging is hoe de puntspreidingsfunctie de beeldvorming in de microscoop beïnvloedt. Het theoretische model van beeldvorming behandelt de point spread functie als de basiseenheid van een beeld. Met andere woorden, de point spread function is voor het beeld wat de baksteen is voor het huis. Het beste wat een beeld ooit kan zijn is een samenstel van “point spread” functies, en het vergroten van de vergroting verandert daar niets aan. Een bekend theoretisch optiekboek (Born and Wolf: Principles of Optics) legt uit: “Het is onmogelijk om details die niet in het primaire beeld aanwezig zijn, naar voren te halen door de sterkte van het oculair te vergroten, want elk element van het primaire beeld is een klein diffractiepatroon, en het eigenlijke beeld, zoals gezien door het oculair, is slechts het geheel van de vergrote beelden van deze patronen”.

Als voorbeeld kan een populatie van subresolutie fluorescerende bolletjes tussen een dekglaasje en een microscoopglaasje worden genomen. Een in-focus beeld van dit specimen onthult een wolk van punten, die eigenlijk een schijf omgeven door een kleine set van ringen (in feite, een Airy schijf; zie figuur 4 (a)). Als dit preparaat iets uit het scherpstelveld wordt gehaald, verschijnt een grotere reeks concentrische ringen op de plaats waar elke stip zich in het scherpstelveld bevond (figuur 4(b)). Wanneer een driedimensionaal beeld van dit preparaat wordt verzameld, wordt voor elke kraal een volledige point spread function opgenomen. De “point spread function” beschrijft wat er met elke punt van licht gebeurt nadat het door het beeldvormingssysteem is gegaan.

Het zojuist beschreven vervagingproces wordt wiskundig gemodelleerd als een convolutie. De convolutie beschrijft de toepassing van de puntspreidingsfunctie op elk punt in het preparaat: het licht van elk punt in het object wordt geconvolveerd met de puntspreidingsfunctie om het uiteindelijke beeld te verkrijgen. Helaas veroorzaakt deze convolutie dat punten in het preparaat wazige gebieden in het beeld worden. De helderheid van elk punt in het beeld wordt door de convolutie lineair gerelateerd aan de fluorescentie van elk punt in het preparaat. Omdat de puntspreidingsfunctie driedimensionaal is, is de onscherpte van de puntspreidingsfunctie een inherent driedimensionaal verschijnsel. Het beeld van een brandvlak bevat onscherp licht van punten die zich in dat vlak bevinden, gemengd met onscherp licht van punten die afkomstig zijn uit andere brandvlakken.

De situatie kan worden samengevat met het idee dat het beeld wordt gevormd door een convolutie van het preparaat met de puntspreidingsfunctie. Deconvolutie keert dit proces om en tracht het specimen te reconstrueren uit een onscherp beeld.

Aberraties in de puntspreidingsfunctie

De puntspreidingsfunctie kan theoretisch worden gedefinieerd door gebruik te maken van een wiskundig model van diffractie, of empirisch door het verkrijgen van een driedimensionaal beeld van een fluorescerende kraal (zie figuur 3). Een theoretische “point spread” functie heeft in het algemeen een axiale en radiale symmetrie. In feite is de “point spread” functie symmetrisch boven en onder het x-y-vlak (axiale symmetrie) en rotatie om de z-as (radiale symmetrie). Een empirische “point spread” functie kan aanzienlijk afwijken van een perfecte symmetrie (zoals weergegeven in figuur 3). Deze afwijking, die aberratie wordt genoemd, wordt veroorzaakt door onregelmatigheden of foutieve uitlijningen in de optische onderdelen van het beeldvormingssysteem, met name in het objectief, maar kan ook optreden bij andere onderdelen zoals spiegels, bundelsplitsers, buislenzen, filters, diafragma’s en diafragma’s. Hoe beter de kwaliteit van de optische componenten en de uitlijning van de microscoop, hoe dichter de empirische “point spread” functie bij haar ideale symmetrische vorm komt. Zowel confocale als deconvolutiemicroscopie zijn afhankelijk van een puntspreidingsfunctie die zo dicht mogelijk bij het ideale geval ligt.

De meest voorkomende aberratie bij optische microscopie, welbekend bij elke ervaren en professionele microscopist, is sferische aberratie. Deze aberratie komt tot uiting in een axiale asymmetrie in de vorm van de “point spread function”, met een overeenkomstige toename van de grootte, vooral langs de z-as (figuur 3). Het resultaat is een aanzienlijk verlies van resolutie en signaalintensiteit. In de praktijk is de typische bron van sferische aberratie een mismatch tussen de brekingsindexen van het immersiemedium van de voorste lens van het objectief en het bevestigingsmedium waarin het specimen is ondergedompeld. Er moet grote nadruk worden gelegd op het belang van het minimaliseren van deze aberratie. Hoewel deconvolutie gedeeltelijk de verloren resolutie kan herstellen, kan geen enkele beeldverwerking het verloren signaal herstellen.