Helmholtz-resonantie
- Analyseren van de Helmholtz-resonantie
- Resonantie, impedantie, fase- en frequentieafhankelijkheid
- Complicaties met de lengte
- Helmholtz-resonanties en gitaren
Analyseren van de Helmholtz-resonantie
Laten we nu eens kwantitatief worden: Allereerst nemen we aan dat de golflengte van het geproduceerde geluid veel langer is dan de afmetingen van de resonator. Voor de flessen in de animatie bovenaan deze pagina is de golflengte respectievelijk 180 en 74 cm, dus deze benadering is vrij goed, maar het is de moeite waard om te controleren wanneer je iets begint te beschrijven als een Helmholtz-oscillator. Het gevolg van deze benadering is dat we drukvariaties binnen het volume van de container kunnen verwaarlozen: de drukoscillatie zal overal binnen de container dezelfde fase hebben.
Stel dat de lucht in de hals een effectieve lengte L en een doorsnede S heeft. De massa is dan SL maal de dichtheid van lucht ρ. (Enkele complicaties met betrekking tot de effectieve lengte worden aan het eind van deze bladzijde besproken). Als deze “plug” van lucht een kleine afstand x in de fles zakt, drukt hij de lucht in de fles samen, zodat de lucht die voorheen volume V innam, nu volume V – Sx heeft. Dientengevolge stijgt de druk van die lucht van de atmosferische druk PA tot een hogere waarde PA + p.
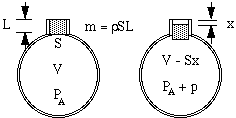
Nu zou je kunnen denken dat de drukstijging gewoon evenredig zou zijn met de volumevermindering. Dat zou het geval zijn als de compressie zo langzaam zou verlopen dat de temperatuur niet zou veranderen. In trillingen die aanleiding geven tot geluid, echter, zijn de veranderingen snel en dus stijgt de temperatuur bij compressie, wat een grotere verandering in druk geeft. Technisch gezien zijn ze adiabatisch, wat betekent dat de warmte geen tijd heeft om te bewegen, en de resulterende vergelijking impliceert een constante γ, de verhouding van de soortelijke warmte, die voor lucht ongeveer 1,4 is. (Dit wordt uitgelegd in een bijlage.) Dientengevolge is de drukverandering p veroorzaakt door een kleine volumeverandering ΔV slechts
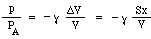
Nu wordt de massa m verplaatst door het drukverschil tussen de bovenkant en de onderkant van de hals, d.w.z. een nettokracht pS, zodat we de wet van Newton schrijven voor de versnelling a:
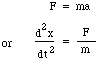
substitutie voor F en m geeft: 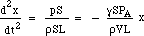
Dus de herstelkracht is evenredig met de verplaatsing. Dit is de voorwaarde voor een Simple Harmonic Motion, en deze heeft een frequentie die 1/2π maal de vierkantswortel van de evenredigheidsconstante is, dus
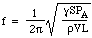
Nu wordt de geluidssnelheid c in lucht bepaald door de dichtheid, de druk en de verhouding van de soortelijke warmte, dus kunnen we schrijven:
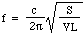
Laten we er wat getallen bij zetten: voor een fles van 1 liter, met S = 3 vierkante centimeter en L = 5 centimeter, is de frequentie 130 Hz, dat is ongeveer de C onder midden C. (Zie noten.) De golflengte is dus 2,6 meter, en dat is veel groter dan de fles. Dit rechtvaardigt, post hoc, de aanname aan het begin van de afleiding.
Resonantie, impedantie, fase- en frequentieafhankelijkheid
Deze paragraaf kan op zichzelf worden gelezen, maar als u meer gedetailleerde achtergrond wilt, zie Oscillaties, Gedwongen oscillaties en Akoestische overeenstemming, inertie en impedantie.
Laten we terugkeren naar de mechanische voorstelling en de Helmholtz resonator van buitenaf bekijken, zoals in het eerste schema: we duwen met een oscillerende kracht F, met frequentie f , de massa m (de lucht in de hals van de resonator), die gesteund wordt op de veer (de ingesloten lucht) met veerconstante k, waarvan het andere uiteinde gefixeerd is (de lucht in de resonator kan niet ontsnappen). Onrealistisch genoeg verwaarlozen we (voorlopig) de zwaartekracht en de wrijving.
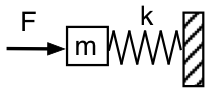
De kracht die nodig is om de massa te versnellen is evenredig met de versnelling en dus evenredig met f2. Bij voldoende lage frequentie is de kracht die nodig is om de massa te versnellen verwaarloosbaar, zodat F alleen de veer hoeft samen te drukken en uit te schuiven. Dus in die limiet is de toegepaste kracht F = +kx. (De veerkracht is -kx.) De mechanische impedantie van het systeem bij deze lage frequentie is volgzaam of veerachtig. Akoestisch ziet het eruit als een akoestische meegaandheid: we duwen de luchtmassa in de hals en persen de lucht in de resonator samen. De uitgeoefende kracht F naar rechts is in fase met x gemeten naar rechts, dus 90° achter de snelheid en de uitgeoefende druk is 90° achter de akoestische stroom in de resonator.
Bedenk dat f2 afhankelijk is van de versnelling. Dus, bij voldoende hoge frequentie, is de veerkracht verwaarloosbaar in vergelijking met de versnelling van de massa. F is dus in fase met de versnelling, waardoor hij 90° voorloopt op de snelheid. Akoestisch gezien ligt de uitgeoefende druk 90° voor op de akoestische stroom in de resonator. Het is een mechanische of akoestische inertie.
Bij de resonantiefrequentie (nog steeds sprekend over de schets hierboven), kan de amplitude groot zijn voor zeer kleine kracht. Dus bij resonantie is de impedantie zeer laag, bezien vanuit de kracht die van buitenaf op de massa wordt uitgeoefend (het schema hierboven). Bij resonantie, is er maximum stroom in en uit de resonator.
Bedenk nu wat er gebeurt als we kijken naar de druk binnenin de resonator (weg van de hals). Hier kijken we naar de kracht op de veer, dus onze mechanische analoog ziet eruit als dit schema.
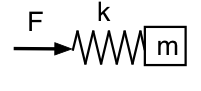
Ditmaal betekent de lage frequentie dat de kracht klein kan zijn voor een gegeven amplitude: de veer en de massa bewegen samen als een massa, en het systeem ziet er ditmaal inert uit bij lage frequentie. Bij hoge frequentie beweegt de massa nauwelijks, en is het systeem veer-achtig of volgzaam. De faserelaties zijn dus tegengesteld aan wat we eerder hadden: bij lage f loopt p 90° voor op U; bij hoge f loopt p 90° achter op U.
Berekeningen met de effectieve lengte
Het eerste diagram op deze bladzijde tekent de “stop” van lucht alsof het een cilinder is die netjes eindigt aan beide uiteinden van de hals van de fles. Dit is overgesimplificeerd. In de praktijk beweegt een extra volume zowel binnen als buiten met de lucht in de hals – zoals in de animatie hierboven wordt gesuggereerd. De extra lengte die aan de geometrische lengte van de hals moet worden toegevoegd, bedraagt gewoonlijk (en zeer bij benadering) 0,6 maal de straal aan het buitenuiteinde, en één straal aan het binnenuiteinde).
|
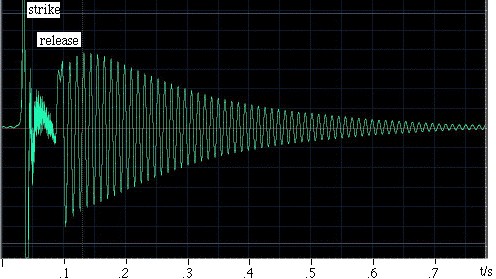
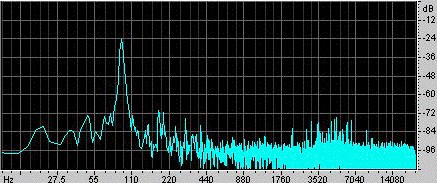
Een voorbeeld. Ra Inta maakte dit voorbeeld. Hij nam een bolvormige Helmholtz-resonator met een volume van 0,00292 m3 en een cilindrische hals met een lengte van 0,080 m en een doorsnede van 0,00083 m2. Om de resonator op te wekken, slaat hij er met de palm van zijn hand op en laat hem dan los. Een microfoon in de resonator registreert het geluid, dat te zien is in het oscillogram links. Men kan zien dat de hand de resonator gedurende iets minder dan 0,1 s afsluit, en dat gedurende deze tijd de oscillaties zwakker zijn en van betrekkelijk hoge frequentie. Zodra de hand wordt losgelaten, ontstaat een oscillatie, die geleidelijk wegsterft naarmate zij energie verliest door viskeuze en turbulente weerstand, en ook door geluidsstraling. Nader onderzoek toont aan dat de frequentie iets toeneemt naarmate de hand zich verwijdert van het open einde, omdat dit de hand de voor straling beschikbare ruimtehoek beperkt en zo het eindeffect (of eindcorrectie) vergroot. De lengte van de hals wordt vergroot met één baffled en één unbaffled eindeffect, waardoor hij een effectieve lengte krijgt van 0,105 m. Met een geluidssnelheid van 343 m/s geeft bovenstaande uitdrukking een resonantiefrequentie van 90 Hz. |
|
Helmholtz-resonanties en gitaren
* Ik zei hierboven dat de lucht in de body van een gitaar zich bijna als een Helmholtz-oscillator gedraagt. Dit geval is gecompliceerd omdat de body een beetje kan opzwellen als de luchtdruk binnenin toeneemt – en ook omdat de lucht “in” het klankgat van de gitaar een geometrie heeft die minder gemakkelijk te visualiseren is dan die in de hals van een fles. In het geval van de gitaarbody is de lengte van de plug van de lucht namelijk ongeveer gelijk aan de twee “eindeffecten” aan het eind van een “pijp” die slechts een paar mm dik is. De eindeffecten zijn echter gerelateerd aan en van vergelijkbare grootte als de straal van het gat, zodat de massa van de lucht aanzienlijk is. De lengte van het eindeffect van een cilindrische pijp die uitkomt op een oneindige, vlakke baffle is 0,85 maal de radius van de pijp. Hoewel de klankkast van een gitaar niet oneindig is, zou men een soortgelijk eindeffect verwachten, en dus zou de effectieve lengte van de “plug” lucht ongeveer 1,7 maal de radius van het gat zijn. (Sommige bouwers vergroten dit door een korte buis onder het klankgat te bevestigen, met gelijke radius).
Een paar mensen hebben geschreven met de vraag hoe groot het klankgat moet zijn voor een bepaald instrument. Welnu, we kunnen de bovenstaande vergelijking gebruiken om die vraag te beantwoorden. Echter, de zwelling van de body is belangrijk. Dit maakt de “veer” van de lucht wat zachter, en verlaagt dus de frequentie. De zuivere Helmholtz-resonantie kan worden onderzocht door het volume van het lichaam constant te houden. Bij het meten hiervan is het gebruikelijk de gitaar in zand te begraven, om de zwelling of ‘ademhaling’ van de body te belemmeren. Gitaren worden echter meestal niet in deze situatie bespeeld. De Helmholtz-berekening zal dus een overschatting geven van de resonantiefrequentie voor een echte, flexibele body.
Laten we uitgaan van een cirkelvormig klankgat met straal r, dus S = πr2, en L = 1,7r zoals hierboven uitgelegd. Wanneer we dit substitueren in de vergelijking voor de Helmholtz-frequentie, met c = 340 m/s, krijgen we:
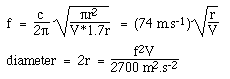
Merk op dat we standaard SI-eenheden gebruiken: we hebben de geluidssnelheid in meters en seconden gebruikt, dus het volume moet in kubieke meters zijn en de frequentie in Hertz, om een antwoord in meters te geven.
Het is ingewikkelder wanneer de toongaten niet cirkelvormig zijn, omdat het eindeffect niet gelijk is aan dat van een cirkel met dezelfde oppervlakte. Doctorandus en gitaarbouwer John McLennan is bezig met een verslag van enkele metingen hierover, dat we hier binnenkort zullen plaatsen.
Op instrumenten uit de gitaar- en vioolfamilie ligt de Helmholtz-resonantie (plus body) vaak in de buurt van of iets onder de frequentie van de op één na laagste snaar, rond D op een viool of G-A op een gitaar. Je kunt de Helmholtz-frequentie aanzienlijk verlagen of verschuiven door het gat geheel of gedeeltelijk af te dekken met een stuk stijf karton met een geschikte vorm. Als je dan een noot speelt in de buurt van de resonantie en dan het karton schuift zodat het afwisselend het gat bedekt en onthult, zul je duidelijk het effect van de resonantie horen.
Is het 0.85r effect redelijk? Ra Inta, die in ons lab gepromoveerd is op gitaarakoestiek, stelt een interessante demonstratie voor:
Demp de snaren van je gitaar zodat ze niet trillen (b.v. een zakdoek tussen snaren en toets). Houd de palm van je ene hand boven het klankgat, en er dicht tegenaan. Sla met een vinger van je andere hand een scherpe slag op de klankkast in de buurt van het klankgat en dicht bij de 1e snaar. U voelt een puls van lucht op de palm van uw hand. De slag van je vinger duwt het klankbord naar binnen en perst wat lucht uit het lichaam. Beweeg nu uw hand geleidelijk verder weg van het gat, en ga door met tikken met de vinger. Wanneer voelt u de beweging van de lucht niet meer? Dit zal u een ruwe schatting geven van de lengte van het “eindeffect” in het geval van het klankgat.
De Helmholtz-resonantie afstemmen
Onder de publicaties van John McLennan, een promovendus in dit lab, is een artikel waarin hij de Helmholtz-resonantie varieert door de snelheid van het geluid te variëren.
- McLennan, J.E. (2003) “A0 and A1 studies on the violin using CO2, He, and air/helium mixtures.” Acustica, 89, 176-180.
Enkele foto’s van historische Helmholtz-resonatoren verstrekt door Thomas B. Greenslade, Kenyon College, Ohio.
Leave a Reply