Green’s Function

Generaliseerd gesproken, is een Groen-functie een integraalkernel die kan worden gebruikt om differentiaalvergelijkingen uit een groot aantal families op te lossen, waaronder eenvoudigere voorbeelden zoals gewone differentiaalvergelijkingen met begin- of randwaardevoorwaarden, maar ook moeilijkere voorbeelden zoals inhomogene partiële differentiaalvergelijkingen (PDE’s) met randvoorwaarden. Groene functies zijn om verschillende redenen belangrijk en maken visuele interpretaties mogelijk van de acties geassocieerd met een krachtbron of met een lading geconcentreerd in een punt (Qin 2014), waardoor ze bijzonder nuttig zijn in gebieden van toegepaste wiskunde. In het bijzonder worden Green’s functiemethoden veel gebruikt in, bijv, natuurkunde, en techniek.

Meer precies, gegeven een lineaire differentiaaloperator handelend op de verzameling van verdelingen over een deelverzameling van een of andere Euclidische ruimte , een Groene functie in het punt dat overeenkomt met is een oplossing van

(1)

waar de deltafunctie aanduidt. De motivatie voor het definiëren van een dergelijke functie is wijdverbreid, maar door de bovenstaande identiteit te vermenigvuldigen met een functie en te integreren met betrekking tot ontstaat

(2)

Het rechterlid reduceert slechts tot vanwege eigenschappen van de deltafunctie, en omdat een lineaire operator is die alleen werkt op en niet op , kan het linkerlid worden herschreven als

(3)

Deze reductie is vooral nuttig bij het oplossen van in differentiaalvergelijkingen van de vorm

(4)

waarbij de bovenstaande rekensom bevestigt dat

(5)

en waaruit volgt dat de specifieke integraalvorm heeft

(6)

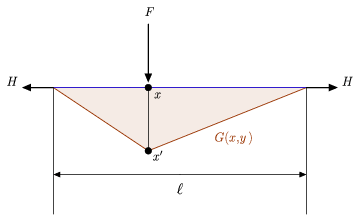
De bovenstaande figuur illustreert zowel de intuïtieve fysische interpretatie van een Groene functie als een relatief eenvoudige bijbehorende differentiaalvergelijking waarmee de bovenstaande definitie kan worden vergeleken (Hartmann 2013). In het bijzonder toont het een strak touw met lengte dat tussen twee muren hangt, op zijn plaats gehouden door een identieke horizontale kracht die op elk van de uiteinden wordt uitgeoefend, en een zijdelingse belasting die op een of ander inwendig punt op het touw wordt geplaatst. Laat het punt zijn dat overeenkomt met op het afgebogen touw, veronderstel dat de neerwaartse kracht constant is, zeg , en laat de afbuiging van het touw zijn. Bij dit natuurkundig systeem hoort de differentiaalvergelijking

(7)

voor met , een stelsel dat zo eenvoudig is dat zowel zijn oplossing als zijn groene functie expliciet kunnen worden geschreven:

(8)

en

(9)

respectievelijk. Zoals uit bovenstaande figuur blijkt, heeft het verplaatste touw het stukgewijs lineaire formaat dat hierboven is gegeven door , waarmee de bewering wordt bevestigd dat de bij dit systeem behorende Groen-functie de werking van het horizontale touw voorstelt die overeenkomt met de toepassing van een kracht .

Een Groen-functie die een paar argumenten neemt, wordt soms een tweepunts-Groen-functie genoemd. Dit in tegenstelling tot meerpunts-Groen’s functies die van bijzonder belang zijn op het gebied van de veellichamentheorie.

Als elementair voorbeeld van een tweepuntsfunctie zoals hierboven gedefinieerd, beschouw het probleem van de bepaling van de potentiaal gegenereerd door een ladingsverdeling waarvan de ladingsdichtheid is, waarbij toepassing van de vergelijking van Poisson en de wet van Coulomb op de potentiaal op geproduceerd door elk element met lading een oplossing oplevert

(10)

hetgeen geldt, onder bepaalde voorwaarden, over het gebied waar . Omdat het rechterlid kan worden gezien als een integraaloperator die omzet in , kan men deze oplossing herschrijven in termen van een Groen-functie van de vorm

(11)

waarbij de oplossing kan worden herschreven:

(12)

(Arfken 2012).

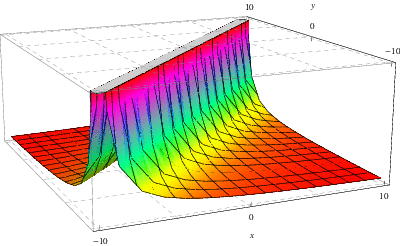
De bovenstaande figuur toont de Groene functie die hoort bij de oplossing van de – vergelijking die hierboven is besproken waar hier, en , respectievelijk , is uitgezet op de -, respectievelijk -, as.

Een enigszins uitgebreide lijst van Groen-functies die corresponderen met verschillende differentiaalvergelijkingen wordt online bijgehouden door Kevin Cole (Cole 2000).

Door de veelheid aan literatuur die over Groen-functies is geschreven, kunnen verschillende notaties en definities naar voren komen, waarvan sommige in topisch opzicht verschillen van de bovenstaande, maar die in het algemeen geen invloed hebben op de belangrijke eigenschappen van de resultaten. Zoals het bovenstaande voorbeeld illustreert, geven sommige auteurs er bijvoorbeeld de voorkeur aan om de variabelen en aan te duiden in termen van vectoren en om te benadrukken dat het elementen zijn van voor een zekere die groter kan zijn dan 1 (Arfken 1985). Het is ook betrekkelijk gebruikelijk om de definitie met een negatief teken te zien, zodat wordt gedefinieerd als de functie waarvoor

(13)

maar omdat deze zuiver fysische beschouwing geen invloed heeft op de onderliggende wiskunde, wordt dit gezichtspunt meestal over het hoofd gezien. Er zijn ook verschillende andere notaties bekend voor een Groene functie, waaronder het gebruik van een kleine letter in plaats van (Stakgold 1979), alsmede het opnemen van een verticale streep in plaats van een komma, bijv, (Duffy 2001).

In andere gevallen presenteert de literatuur definities die nauw verbonden zijn met de context waarin ze worden gepresenteerd. Zo definiëren sommige auteurs Groene functies als functies die aan een bepaalde reeks voorwaarden voldoen, b.v. bestaan op een speciaal soort domein, associatie met een zeer bepaalde differentiaaloperator , of voldoen aan een precieze reeks randvoorwaarden. Een van de meest voorkomende voorbeelden is te vinden in aantekeningen van bijv, Speck, waar een Groene functie gedefinieerd is om te voldoen aan voor punten en voor alle punten die in het grensgebied van liggen (Speck 2011). Deze specifieke definitie stelt een integraalkern voor die overeenkomt met de oplossing van een veralgemeende Poisson-vergelijking, en zou dus duidelijke beperkingen ondervinden wanneer ze wordt aangepast aan een meer algemene setting. Aan de andere kant zijn dergelijke voorbeelden niet zonder hun voordelen. In het geval van het bovenstaande veralgemeende Poisson-voorbeeld bijvoorbeeld kan elk van dergelijke Groen-functies zo worden gesplitst dat

(14)

waar en voor de reguliere Laplaciaan (Hartman 2013). In dergelijke situaties staat bekend als de fundamentele oplossing van de onderliggende differentiaalvergelijking en staat bekend als de reguliere oplossing ervan; als zodanig worden en soms respectievelijk het fundamentele en het reguliere deel van genoemd.

Een aantal fundamentele eigenschappen van een algemene Groen-functie volgt onmiddellijk (of bijna onmiddellijk) uit de definitie ervan en geldt voor alle bijzondere gevallen. Bijvoorbeeld, als de kern van de operator niet-triviaal is, dan kunnen er meerdere Groen-functies geassocieerd zijn met één operator; bijgevolg moet men voorzichtig zijn wanneer men spreekt over “de” Groen-functie. Groene functies voldoen aan een adjunct-symmetrie in hun twee argumenten, zodat

(15)

waarbij is gedefinieerd als de oplossing van de vergelijking

(16)

Hierbij is het adjunct van . Een onmiddellijk gevolg van dit feit is dat voor zelfadjuncte operatoren , symmetrisch is:

(17)

Deze identiteit wordt vaak het wederkerigheidsbeginsel genoemd en zegt, in fysische termen, dat de respons bij veroorzaakt door een eenheidsbron bij dezelfde is als de respons bij veroorzaakt door een eenheidskracht bij (Stakgold 1979).

De essentiële eigenschap van elke Groen-functie is dat zij een manier biedt om de responsie te beschrijven van een willekeurige differentiaalvergelijkingsoplossing op een of andere bronterm in aanwezigheid van een aantal randvoorwaarden (Arfken et al. 2012). Sommige auteurs beschouwen een functie van Groen als een functie die in de theorie van partiële differentiaalvergelijkingen ongeveer dezelfde rol speelt als Fourierreeksen in de oplossing van gewone differentiaalvergelijkingen (Mikula en Kos 2006).

Voor meer abstracte scenario’s bestaan er een aantal concepten die dienen als contextspecifieke analogen van het begrip functie van Groen. Zo is het in de functionele analyse vaak nuttig om een zogenaamde veralgemeende functie van Green te beschouwen, die veel analoge eigenschappen heeft wanneer zij abstract wordt geïntegreerd tegen functionalen in plaats van functies. Dergelijke veralgemeningen hebben inderdaad een geheel analoge tak van theoretische PDE-analyse opgeleverd en zijn zelf het onderwerp van een grote hoeveelheid onderzoek.