Articles /

Gram-Schmidt-proces

door Marco Taboga, PhD

Het Gram-Schmidt-proces (of de Gram-Schmidt-procedure) is een reeks bewerkingen die het mogelijk maakt een verzameling lineair onafhankelijke vectoren om te zetten in een verzameling orthonormale vectoren die dezelfde ruimte beslaan als de oorspronkelijke verzameling.

Inhoudsopgave

Peliminaria

Laat ons enkele begrippen overlopen die essentieel zijn om het Gram-Schmidt-proces te begrijpen.

Bedenk dat twee vectoren $r$ en $s$ orthogonaal zijn als en slechts als hun inwendig product gelijk is aan nul, dat wil zeggen,

Gegeven een inwendig product, kunnen we de norm (lengte) van een vector $s$ als volgt definiëren:

Een verzameling vectoren heet orthonormaal als en slechts als de elementen ervan eenheidsnorm hebben en orthogonaal ten opzichte van elkaar zijn. Met andere woorden, een verzameling van K vectoren is orthonormaal als en slechts als

We hebben bewezen dat de vectoren van een orthonormale verzameling lineair onafhankelijk zijn.

Wanneer een basis voor een vectorruimte ook een orthonormale verzameling is, wordt deze een orthonormale basis genoemd.

Projecties op orthonormale verzamelingen

In het Gram-Schmidt-proces gebruiken we herhaaldelijk de volgende stelling, waaruit blijkt dat elke vector in twee delen kan worden ontleed: 1) zijn projectie op een orthonormale verzameling en 2) een rest die orthogonaal is aan de gegeven orthonormale verzameling.

Stelling Laat $S$ een vectorruimte zijn, voorzien van een inwendig product . Zij een orthonormale verzameling. Voor elke $sin S$ hebben wewaar $arepsilon _{S}$ orthogonaal is aan $u_{k}$ voor elke $k=1,ldots,K.$

Proof

DefinieerDan hebben we voor elke $j=1,ldots,K$ datwaar: in de stappen $rame{A}$ en $rame{B}$ hebben we gebruik gemaakt van het feit dat het binnenproduct lineair is in zijn eerste argument; in stap $rame{C}$ hebben we gebruik gemaakt van het feit dat als $keq j$ aangezien we te maken hebben met een orthonormale verzameling; in stap $rame{D}$ hebben we gebruik gemaakt van het feit dat de norm van $u_{j}$ gelijk is aan 1. Daarom is $arepsilon _{S}$, zoals hierboven gedefinieerd, orthogonaal voor alle elementen van de orthonormale verzameling, hetgeen de stelling bewijst.

De term heet de lineaire projectie van $s$ op de orthonormale verzameling , terwijl de term $arepsilon _{S}$ de rest van de lineaire projectie wordt genoemd.

Normalisatie

Een ander wellicht voor de hand liggend feit dat we herhaaldelijk zullen gebruiken in het Gram-Schmidt proces is dat, als we een willekeurige vector nemen die niet nul is en we delen hem door zijn norm, het resultaat van de deling een nieuwe vector is die eenheidsnorm heeft.

Met andere woorden, als dan hebben we, door de definitiviteitseigenschap van de norm, dat

Als gevolg daarvan kunnen we definiëren en, door de positiviteit en absolute homogeniteit van de norm, hebben we

Overzicht van de procedure

Nu we weten hoe we een vector kunnen normaliseren en hoe we hem kunnen ontbinden in een projectie op een orthonormale verzameling en een residu, zijn we klaar om de Gram-Schmidt-procedure uit te leggen.

We gaan een overzicht geven van het proces, waarna we het formeel zullen uitdrukken als een stelling en we alle technische details zullen bespreken in het bewijs van de stelling.

Hier volgt het overzicht.

We krijgen een verzameling lineair onafhankelijke vectoren .

Om het proces te beginnen normaliseren we de eerste vector, dat wil zeggen we definiëren

In de tweede stap projecteren we $s_{2}$ op $u_{1}$: waarbij $arepsilon _{2}$ de rest van de projectie is.

Vervolgens normaliseren we het residu:

We zullen later bewijzen dat (zodat de normalisatie kan worden uitgevoerd) omdat de startvectoren lineair onafhankelijk zijn.

De twee aldus verkregen vectoren $u_{1}$ en $u_{2}$ zijn orthonormaal.

In de derde stap projecteren we $s_{3}$ op $u_{1}$ en $u_{2}$: en berekenen we het residu van de projectie $arepsilon _{3}$.

Daarna normaliseren we het:

Zo gaan we door tot we het laatste genormaliseerde residu $u_{K} $ hebben.

Aan het eind van het proces vormen de vectoren een orthonormale verzameling omdat:

  1. zij het resultaat zijn van een normalisatie, en bijgevolg eenheidsnorm hebben;

  2. elk $u_{k}$ wordt verkregen uit een residu dat de eigenschap heeft orthogonaal te zijn aan .

Ter vervollediging van dit overzicht herinneren wij eraan dat de lineaire spanwijdte van de verzameling is van alle vectoren die kunnen worden geschreven als lineaire combinaties van ; zij wordt aangeduid met en is een lineaire ruimte.

Daar de vectoren lineair onafhankelijke combinaties zijn van , kan elke vector die kan worden geschreven als een lineaire combinatie van , ook worden geschreven als een lineaire combinatie van . Daarom vallen de spanwijdtes van de twee verzamelingen vectoren samen:

Formele verklaring

We formaliseren hier het Gram-Schmidt proces als een stelling, waarvan het bewijs alle technische details van de procedure bevat.

Stelling Laat $S$ een vectorruimte zijn, voorzien van een inwendig product . Zij lineair onafhankelijke vectoren. Dan bestaat er een verzameling orthonormale vectoren zodanig datvoor elke $kleq K$.

Bewijs

Het bewijs gaat via inductie: eerst bewijzen we dat de stelling waar is voor $k=1$, en dan bewijzen we dat ze waar is voor een generieke k als ze geldt voor $k-1$. Als $k=1$, heeft de vector eenheidsnorm en vormt hij op zichzelf een orthonormale verzameling: er zijn geen andere vectoren, dus aan de orthogonaliteitsvoorwaarde wordt triviaal voldaan. De verzameling is de verzameling van alle scalaire veelvouden van $s_{1}$, die ook scalaire veelvouden zijn van $u_{1}$ (en vice versa). Daarom Nu, stel dat de stelling waar is voor $k-1$. Dan kunnen we $s_{k}$ projecteren op : waarbij het residu $arepsilon _{k}$ orthogonaal is aan . Stel dat $arepsilon _{k}=0$. Dan geldt,Omdat voor elke $jleq k-1$, voor elke $jleq k-1$, waarbij $lpha _{jl}$ scalaren zijn. Daarom,Met andere woorden, de aanname dat $arepsilon _{k}=0$ leidt tot de conclusie dat $s_{k}$ een lineaire combinatie is van . Maar dit is onmogelijk omdat een van de aannames van de stelling is dat lineair onafhankelijk zijn. Bijgevolg moet het zo zijn dat . We kunnen dus het residu normaliseren en de vector definiëren die eenheidsnorm heeft. We weten al dat $arepsilon _{k}$ orthogonaal is aan . Dit impliceert dat ook $u_{k}$ orthogonaal is aan . is dus een orthonormale verzameling. Neem nu een willekeurige vector $sin S$ die geschreven kan worden als waarbij scalaren zijn. 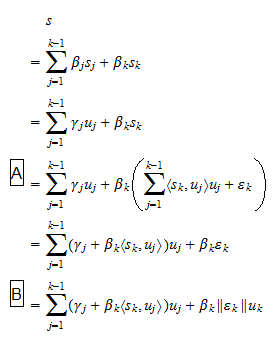Aangezien, door aanname, hebben we dat vergelijking (2) ook geschreven kan worden alswaar scalaren zijn, en: in stap $rame{A}$ hebben we vergelijking (1) gebruikt; in stap $rame{B}$ hebben we de definitie van $u_{k}$ gebruikt. Aldus hebben we bewezen dat elke vector die kan worden geschreven als een lineaire combinatie van ook kan worden geschreven als een lineaire combinatie van . Veronderstelling (3) laat toe om het omgekeerde op een volledig analoge manier te bewijzen: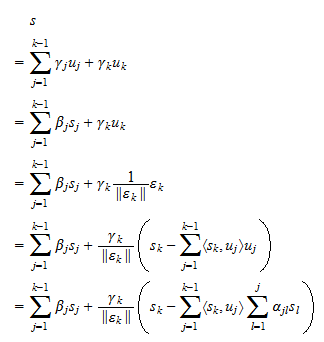Met andere woorden, elke lineaire combinatie van is ook een lineaire combinatie van . Dit bewijst dat en sluit het bewijs af.

Elke binnenproductruimte heeft een orthonormale basis

De volgende stelling geeft een belangrijk gevolg van het Gram-Schmidtproces.

Stelling Stel $S$ is een vectorruimte voorzien van een binnenproduct . Als $S$ een eindige dimensie heeft, dan bestaat er een orthonormale basis voor $S$.

Proof

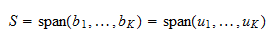Omdat $S$ eindig-dimensionaal is, bestaat er minstens één basis voor $S$, bestaande uit K vectoren . We kunnen de Gram-Schmidt procedure toepassen op de basis en zo een orthonormale verzameling verkrijgen. Omdat een basis is, overspant deze $S$. Dus is een orthonormale basis van $S$.

Oplossingen

Hieronder vindt u enkele oefeningen met toegelichte oplossingen.

Oefening 1

Beschouw de ruimte $S$ van alle $3imes 1$ vectoren met reele ingangen en het inwendig productwaar $r,sin S$ en $s^{op }$ de getransponeerde is van $s$. Definieer de vector

Normaliseer $s$.

Oplossing

De norm van $s$ isDaarom, is de normalisatie van $s$

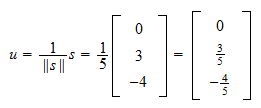
Oefening 2

Beschouw de ruimte $S$ van alle $2imes 1$ vectoren met reële ingangen en het inwendig productwaar $r,sin S$ . Beschouw de twee lineair onafhankelijke vectoren

Verander ze in een orthonormale verzameling met behulp van het Gram-Schmidt-proces.

Oplossing

De norm van $s_{1}$ is Daarom, is de eerste orthonormale vectorHet binnenproduct van $s_{2}$ en $u_{1}$ is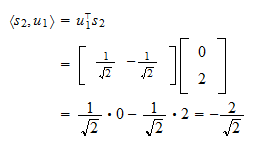De projectie van $s_{2}$ op $u_{1}$ is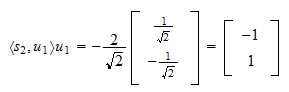Het residu van de projectie is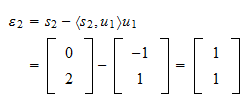De norm van het residu isen het genormaliseerde residu isDus, de orthonormale verzameling die we zochten is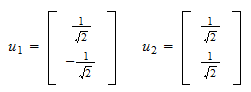

Hoe citeren

Aan te halen als:

Taboga, Marco (2017). “Gram-Schmidt proces”, Lezingen over matrixalgebra. https://www.statlect.com/matrix-algebra/Gram-Schmidt-process.

Leave a Reply