Gibbs Sampling

Zoals andere MCMC-methoden, construeert de Gibbs-sampler een Markov-keten waarvan de waarden convergeren naar een doelverdeling. Gibbs Sampling is in feite een specifiek geval van het Metropolis-Hastings algoritme waarin voorstellen altijd worden geaccepteerd.

Op de keper beschouwd, stel dat u een multivariate kansverdeling wilt bemonsteren.

Note: Een multivariate kansverdeling is een functie van meerdere variabelen (d.w.z. 2 dimensionale normale verdeling).

We weten niet hoe we rechtstreeks van deze laatste kunnen bemonsteren. Maar door wiskundig gemak of misschien gewoon geluk kennen we toevallig de voorwaardelijke kansen.

Dit is waar Gibbs Sampling om de hoek komt kijken. Gibbs Sampling is van toepassing wanneer de gezamenlijke verdeling niet expliciet bekend is of moeilijk rechtstreeks te bemonsteren is, maar de voorwaardelijke verdeling van elke variabele bekend is en gemakkelijker te bemonsteren is.

We beginnen met het kiezen van een beginwaarde voor de willekeurige variabelen X & Y. Vervolgens bemonsteren we uit de voorwaardelijke kansverdeling van X gegeven Y = Y⁰, aangeduid als p(X|Y⁰). In de volgende stap bemonsteren we een nieuwe waarde van Y, afhankelijk van X¹, die we zojuist hebben berekend. We herhalen de procedure voor nog eens n – 1 iteraties, waarbij we afwisselend een nieuwe steekproef trekken uit de voorwaardelijke kansverdeling van X en de voorwaardelijke kansverdeling van Y, gegeven de huidige waarde van de andere willekeurige variabele.

Laten we eens kijken naar een voorbeeld. Stel dat we de volgende posterior en conditionele kansverdelingen hadden.

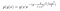
waar g(y) de termen bevat waar x niet in voorkomt, en g(x) de termen bevat die niet van y afhangen.

We kennen de waarde van C (de normaliseringsconstante) niet. Maar we kennen wel de voorwaardelijke kansverdelingen. Daarom kunnen we Gibbs Sampling gebruiken om de posterior verdeling te benaderen.

Note: De voorwaardelijke kansverdelingen zijn in feite normale verdelingen, en kunnen als volgt worden herschreven.

Gegeven de voorgaande vergelijkingen, gaan we verder met het implementeren van het Gibbs Sampling algoritme in Python. Om te beginnen importeren we de volgende bibliotheken.

import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
sns.set()

We definiëren de functie voor de posterior verdeling (neem aan dat C=1).

f = lambda x, y: np.exp(-(x*x*y*y+x*x+y*y-8*x-8*y)/2.)

Daarna plotten we de kansverdeling.

xx = np.linspace(-1, 8, 100)
yy = np.linspace(-1, 8, 100)
xg,yg = np.meshgrid(xx, yy)
z = f(xg.ravel(), yg.ravel())
z2 = z.reshape(xg.shape)
plt.contourf(xg, yg, z2, cmap='BrBG')

Nu gaan we proberen om de kansverdeling te schatten met behulp van Gibbs Sampling. Zoals we eerder hebben vermeld, zijn de voorwaardelijke waarschijnlijkheden normale verdelingen. Daarom kunnen we ze uitdrukken in termen van mu en sigma.

In het volgende blok code definiëren we functies voor mu en sigma, initialiseren we onze willekeurige variabelen X & Y, en stellen we N in (het aantal iteraties).

N = 50000
x = np.zeros(N+1)
y = np.zeros(N+1)
x = 1.
y = 6.
sig = lambda z, i: np.sqrt(1./(1.+z*z))
mu = lambda z, i: 4./(1.+z*z)

We doorlopen het Gibbs Sampling-algoritme.

for i in range(1, N, 2):
sig_x = sig(y, i-1)
mu_x = mu(y, i-1)
x = np.random.normal(mu_x, sig_x)
y = y
sig_y = sig(x, i)
mu_y = mu(x, i)
y = np.random.normal(mu_y, sig_y)
x = x

Tot slot zetten we de resultaten op een kaart.

plt.hist(x, bins=50);
plt.hist(y, bins=50);

plt.contourf(xg, yg, z2, alpha=0.8, cmap='BrBG')
plt.plot(x,y, '.', alpha=0.1)
plt.plot(x,y, c='r', alpha=0.3, lw=1)

Zoals we kunnen zien, dat de kansverdeling die met het Gibbs Sampling-algoritme is verkregen, de doelverdeling goed benadert.

Conclusie

De Gibbs Sampling is een Monte Carlo Markov Chain methode die iteratief een instantie trekt uit de verdeling van elke variabele, voorwaardelijk voor de huidige waarden van de andere variabelen, om complexe gezamenlijke verdelingen te schatten. In tegenstelling tot het Metropolis-Hastings algoritme wordt het voorstel altijd aanvaard. Gibbs Sampling kan dus veel efficiënter zijn.