Friedman Test in SPSS Statistics

SPSS Statistics

SPSS Statistics Output for the Friedman Test

SPSS Statistics genereert twee of drie tabellen, afhankelijk van of u descriptives en/of kwartielen wilt laten genereren naast het uitvoeren van de Friedman test.

Descriptieve Statistiekentabel

De tabel met beschrijvende statistische gegevens wordt gegenereerd als u de optie kwartielen hebt geselecteerd:

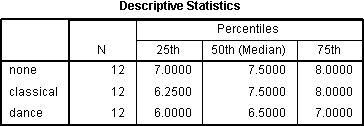
Gepubliceerd met schriftelijke toestemming van SPSS Statistics, IBM Corporation.

Dit is een zeer nuttige tabel omdat hij kan worden gebruikt om beschrijvende statistieken te presenteren in uw resultatensectie voor elk van de tijdstippen of condities (afhankelijk van uw onderzoeksopzet) voor uw afhankelijke variabele. Dit nut zal later worden gepresenteerd in het gedeelte “Rapportage van de output”.

Rangentabel

De rangentabel toont de gemiddelde rang voor elk van de gerelateerde groepen, zoals hieronder getoond:

Gepubliceerd met schriftelijke toestemming van SPSS Statistics, IBM Corporation.

De Friedman-test vergelijkt de gemiddelde rangorde tussen de verwante groepen en geeft aan hoe de groepen van elkaar verschilden, en is daarom opgenomen. Het is echter niet erg waarschijnlijk dat u deze waarden daadwerkelijk in uw resultatensectie rapporteert, maar waarschijnlijk zult u de mediaanwaarde voor elke verwante groep rapporteren.

Teststatistiekentabel

De tabel Teststatistieken informeert u over het werkelijke resultaat van de Friedman-test, en of er een algemeen statistisch significant verschil was tussen de gemiddelde rangschikkingen van uw verwante groepen. Voor het voorbeeld dat in deze handleiding wordt gebruikt, ziet de tabel er als volgt uit:

Gepubliceerd met schriftelijke toestemming van SPSS Statistics, IBM Corporation.

De bovenstaande tabel geeft de teststatistische waarde (χ2) (“Chi-kwadraat”), vrijheidsgraden (“df”) en het significantieniveau (“Asymp. Sig.”), en dat is alles wat we nodig hebben om het resultaat van de Friedman-test te rapporteren. Uit ons voorbeeld kunnen we afleiden dat er een algemeen statistisch significant verschil is tussen de gemiddelde rangen van de verwante groepen. Het is belangrijk op te merken dat de Friedman test een omnibus test is, net als zijn parametrisch alternatief; dat wil zeggen dat hij u vertelt of er algemene verschillen zijn, maar niet precies aangeeft welke groepen in het bijzonder van elkaar verschillen. Om dit te doen moet u post hoc tests uitvoeren, die na de volgende sectie zullen worden besproken.

SPSS Statistics

Reporting the Output of the Friedman Test (without post hoc tests)

U kunt het resultaat van de Friedman test als volgt rapporteren:

U zou ook de mediaanwaarden voor elk van de verwante groepen kunnen opnemen. In dit stadium weet u echter alleen dat er ergens verschillen zijn tussen de verwante groepen, maar u weet niet precies waar die verschillen liggen. Vergeet echter niet dat als het resultaat van uw Friedman-test statistisch niet significant was, u geen post-hoc-tests moet uitvoeren.

Post-hoc-tests

Om te onderzoeken waar de verschillen zich werkelijk voordoen, moet u afzonderlijke Wilcoxon signed-rank-tests uitvoeren op de verschillende combinaties van verwante groepen. In dit voorbeeld zou u dus de volgende combinaties vergelijken:

• Niemand met Klassiek.
• Niemand met Dans.
• Klassiek met Dans.

U moet een Bonferroni-aanpassing gebruiken voor de resultaten die u met de Wilcoxon-tests krijgt, omdat u meerdere vergelijkingen maakt, waardoor de kans groter is dat u een resultaat significant verklaart terwijl dat niet zou moeten (een Type I-fout). Gelukkig is de Bonferroni-aanpassing heel eenvoudig te berekenen; neem gewoon het significantieniveau dat u aanvankelijk gebruikte (in dit geval 0,05) en deel het door het aantal tests dat u uitvoert. In dit voorbeeld hebben we dus een nieuw significantieniveau van 0.05/3 = 0.017. Dit betekent dat als de p-waarde groter is dan 0,017, we geen statistisch significant resultaat hebben.

Uitvoeren van deze tests (zie hoe met onze Wilcoxon signed-rank test gids) op de resultaten van dit voorbeeld, krijgt u het volgende resultaat:

Gepubliceerd met schriftelijke toestemming van SPSS Statistics, IBM Corporation.

Deze tabel toont de uitvoer van de Wilcoxon signed-rank test op elk van onze combinaties. Het is belangrijk op te merken dat de significantiewaarden in SPSS Statistics niet zijn aangepast om te compenseren voor meervoudige vergelijkingen – u moet de door SPSS Statistics geproduceerde significantiewaarden handmatig vergelijken met het door u berekende, voor Bonferroni-aanpassing gecorrigeerde significantieniveau. We kunnen zien dat op het significantieniveau p < 0,017 alleen de waargenomen inspanning tussen geen muziek en dans (dans-niet, p = 0,008) statistisch significant verschillend was.

SPSS Statistics

Reporting the Output of the Friedman Test (with post hoc tests)

U kunt de resultaten van de Friedman test met post hoc tests als volgt rapporteren: