Een voorzichtige inleiding tot het convexe-romp probleem

Convexe-rompen blijken op veel verschillende terreinen nuttig te zijn, soms heel onverwacht. In dit artikel zal ik de basisideeën van 2d convexe rompen uitleggen en hoe je de graham scan kunt gebruiken om ze te vinden. Dus als je de graham scan al kent, dan is dit artikel niet voor jou, maar zo niet, dan zou dit je vertrouwd moeten maken met enkele van de relevante concepten.

De convexe schil van een verzameling punten wordt gedefinieerd als de kleinste convexe veelhoek, die alle punten in de verzameling omvat. Convex betekent dat de veelhoek geen hoek heeft die naar binnen is gebogen.

De rode randen op de rechter veelhoek omsluiten de hoek waar de vorm concaaf is, het tegenovergestelde van convex.

Een handige manier om over de convexe schil na te denken is de elastiekjesanalogie. Stel dat de punten in de verzameling spijkers waren, die uit een plat vlak staken. Stel je nu eens voor wat er zou gebeuren als je een elastiekje zou nemen en het rond de spijkers zou spannen. Als je probeert het elastiekje terug te trekken tot zijn oorspronkelijke lengte, zal het de spijkers omsluiten en de spijkers raken die het verst van het midden uitsteken.

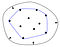
Om de resulterende convexe romp in code weer te geven, slaan we gewoonlijk de lijst van punten op die dit elastiekje omhoog houden, d.w.z. de lijst van punten op de convexe romp.

Merk op dat we nog moeten definiëren wat er moet gebeuren als drie punten op dezelfde lijn liggen. Als je je voorstelt dat het elastiekje een punt heeft waar het een van de spijkers raakt, maar daar helemaal niet buigt, dan betekent dat dat de spijker daar op een rechte lijn ligt tussen twee andere spijkers. Afhankelijk van het probleem kunnen we deze spijker op de rechte lijn beschouwen als een deel van de uitvoer, omdat hij het elastiekje raakt. Aan de andere kant kunnen we ook zeggen dat deze spijker geen deel uitmaakt van de uitvoer, omdat de vorm van het elastiekje niet verandert als we het weghalen. Deze beslissing hangt af van het probleem waar je op dat moment mee bezig bent, en het beste is als je een invoer hebt waarbij geen drie punten collineair zijn (dit is vaak het geval bij eenvoudige opgaven voor programmeerwedstrijden) dan kun je dit probleem zelfs volledig negeren.

Vinden van de convexe romp

Kijkend naar een verzameling punten laat de menselijke intuïtie ons snel uitzoeken welke punten waarschijnlijk de convexe romp zullen raken, en welke punten dichter bij het centrum en dus weg van de convexe romp zullen liggen. Maar het vertalen van deze intuïtie in code vergt wat werk.

Om de convexe romp van een verzameling punten te vinden, kunnen we een algoritme gebruiken dat de Graham Scan wordt genoemd, en dat wordt beschouwd als een van de eerste algoritmen van computationele meetkunde. Met behulp van dit algoritme kan men de deelverzameling van punten vinden die op de convexe schil liggen, samen met de volgorde waarin men deze punten tegenkomt als men rond de convexe schil gaat.

Het algoritme begint met het vinden van een punt, waarvan men zeker weet dat het op de convexe schil ligt. Het punt met de laagste y-coördinaat bijvoorbeeld kan als een veilige keuze worden beschouwd. Als er meerdere punten op dezelfde y-coördinaat liggen, nemen we het punt met de grootste x-coördinaat (dit werkt ook met andere hoekpunten, b.v. eerst laagste x dan laagste y).

Na het beginpunt sorteren we de andere punten op de hoek waaronder ze liggen, gezien vanuit het beginpunt. Als twee punten toevallig onder dezelfde hoek liggen, moet het punt dat het dichtst bij het beginpunt ligt, eerder in de sortering voorkomen.

Nu is het de bedoeling van het algoritme om rond deze gesorteerde matrix te lopen en voor elk punt te bepalen of het al dan niet op de convexe schil ligt. Dit betekent, dat voor elk drievoud van punten die we tegenkomen, we beslissen of ze een convexe of een concave hoek vormen. Als de hoek concaaf is, dan weten we, dat het middelste punt uit dit drietal niet op de convexe schil kan liggen.

(Merk op, dat de termen concave en convexe hoek moeten worden gebruikt in relatie tot de gehele veelhoek, alleen een hoek op zichzelf kan niet convex of concaaf zijn, omdat er dan geen referentierichting is.)

We slaan de punten die op de convexe schil liggen op een stapel op, op die manier kunnen we punten toevoegen als we ze bereiken op onze weg rond de gesorteerde punten, en ze verwijderen als we erachter komen dat ze een concave hoek vormen.

(Strikt genomen moeten we toegang hebben tot de bovenste twee punten van de stapel, daarom gebruiken we in plaats daarvan een std::vector, maar we zien het als een soort stapel, omdat we ons altijd alleen met de bovenste paar elementen bezighouden.)

Weggaand rond de gesorteerde rij punten, voegen we het punt toe aan de stapel, en als we later ontdekken dat het punt niet tot de convexe schil behoort, verwijderen we het.

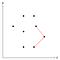
We kunnen meten of de huidige hoek naar binnen of naar buiten buigt door het kruisproduct te berekenen en te kijken of dat positief of negatief is. De figuur hierboven toont een drietal punten waarvan de hoek die ze vormen convex is, daarom blijft het middelste van deze drie punten voorlopig op de stapel.

Op naar het volgende punt gaan we op dezelfde manier te werk: controleren of de hoek convex is en zo niet, het punt verwijderen. Vervolgens voegen we het volgende punt toe en herhalen dit.

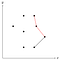
Deze in rood gemarkeerde hoek is concaaf, daarom verwijderen we het middelste punt uit de stapel omdat het geen deel kan uitmaken van de convexe schil.

Hoe weten we dat dit het juiste antwoord oplevert?

Het schrijven van een rigoureus bewijs valt buiten het bestek van dit artikel, maar ik kan de basisideeën opschrijven. Ik moedig u echter aan om verder te gaan en te proberen de gaten in te vullen!

Omdat we het kruisproduct op elke hoek hebben berekend, weten we zeker dat we een convexe veelhoek krijgen. Nu moeten we alleen nog bewijzen, dat deze convexe veelhoek werkelijk alle punten insluit.

(Eigenlijk zou je ook moeten aantonen, dat dit de kleinst mogelijke convexe veelhoek is, die aan deze voorwaarden voldoet, maar dat volgt vrij gemakkelijk uit het feit, dat de hoekpunten van onze convexe veelhoek een deelverzameling zijn van de oorspronkelijke verzameling punten.)

Voorstel, dat er een punt P bestaat buiten de veelhoek die we zojuist hebben gevonden.

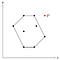
Omdat elk punt eenmaal aan de stapel is toegevoegd, weten we dat P op enig moment van de stapel is verwijderd. Dit betekent, dat P samen met zijn naburige punten, laten we ze O en Q noemen, een concave hoek vormde.

Omdat O en Q binnen de veelhoek liggen (of op de grens ervan), zou P ook binnen de grens moeten liggen, want de veelhoek is convex en de hoek die O en Q met P vormen is concaaf ten opzichte van de veelhoek.

Dus hebben we een tegenstrijdigheid gevonden, wat betekent dat zo’n punt P niet kan bestaan.

Implementatie

De hier gegeven implementatie heeft een functie convex_hull, die een std::vector neemt die de punten bevat als std::pairs van ints en een andere std::vector teruggeeft die de punten bevat die op de convexe romp liggen.

Runtime en geheugenanalyse

Het is altijd nuttig om over de complexiteitsalgoritmen na te denken in termen van de Big-O notatie, die ik hier niet zal uitleggen, omdat Michael Olorunnisola het hier al veel beter heeft uitgelegd dan ik waarschijnlijk zou doen:

Het sorteren van de punten kost aanvankelijk O(n log n) tijd, maar daarna kan elke stap in constante tijd worden berekend. Elk punt wordt hoogstens eenmaal aan de stack toegevoegd en er weer uitgehaald, wat betekent dat de worst-case runtime in O(n log n) ligt.

Het geheugengebruik, dat nu in O(n) ligt, zou geoptimaliseerd kunnen worden door de stack overbodig te maken en de bewerkingen direct op de input array uit te voeren. We zouden de punten die op de convexe schil liggen naar het begin van de invoer-array kunnen verplaatsen en ze in de juiste volgorde rangschikken, en de andere punten zouden naar de rest van de array worden verplaatst. De functie zou dan slechts een enkele gehele variabele kunnen teruggeven die het aantal punten in de matrix weergeeft dat op de convexe romp ligt. Dit heeft natuurlijk het nadeel dat de functie veel gecompliceerder wordt, en ik zou het daarom afraden, tenzij je codeert voor embedded systemen of gelijkaardige beperkende geheugenoverwegingen hebt. Voor de meeste situaties is de kans op fouten/geheugenbesparing het gewoon niet waard.

Andere algoritmen

Een alternatief voor de Graham Scan is Chan’s algoritme, dat in feite op hetzelfde idee is gebaseerd, maar eenvoudiger te implementeren is. Het is echter zinvol om eerst te begrijpen hoe de Graham Scan werkt.

Als je echt zin hebt en het probleem in drie dimensies wilt aanpakken, kijk dan eens naar het algoritme van Preparata en Hong dat zij introduceerden in hun paper “Convex Hulls of Finite Sets of Points in Two and Three Dimensions” uit 1977.