Bilineaire filtering & bilineaire interpolatie

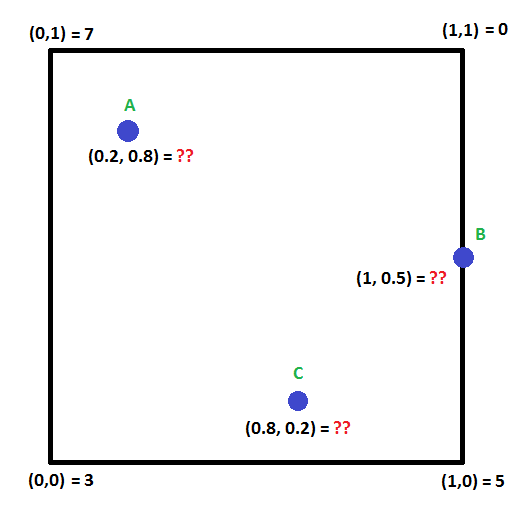
Kijk eens naar het plaatje hieronder. Kun je de waarden in de punten A,B en C berekenen?

Er is een techniek om dit te doen die bilineaire interpolatie heet en die het idee van lineaire interpolatie uitbreidt naar twee dimensies.

Om bilineaire interpolatie te berekenen, doe je gewoon lineaire interpolatie op één as, en dan de andere.

Kijk eens naar deze voorbeelden:

Punt A
Punt A heeft een coördinaat van (0,2,0,8). Laten we beginnen met de X-as.

Eerst doen we interpolatie over de top van het vierkant op de X-as. Dat betekent dat we 0,2 (20%) van de weg van 7 naar 0 moeten gaan. Die 0,2 is onze x-as coördinaat. Om dat te berekenen doen we het volgende:
7 + (0-7) * 0.2 = 5.6

Volgende doen we interpolatie over de onderkant van het vierkant op de X-as. Dus net als hierboven gaan we 0,2 (20%) van de weg van 3 naar 5. Om dat te berekenen doen we het volgende:
3 + (5-3) * 0.2 = 3.4

Nu we over onze X-as hebben geïnterpoleerd, moeten we interpoleren over onze Y-as. We gaan nu 0.8 (80%) van de weg van onze onderste waarde (de waarde van Y = 0), naar onze bovenste waarde (de waarde van Y = 1). De onderste waarde is de onderste interpolatie die we hebben gedaan (3.4) en de bovenste waarde is de bovenste interpolatie die we hebben gedaan (5.6).

Dus, we moeten 0.8 (80%) van de weg van 3.4 naar 5.6 gaan. Om dat te berekenen doen we het volgende:
3,4 + (5,6 – 3,4) * 0,8 = 5,16

Dus, de waarde in punt A is 5,16. De onderstaande afbeelding moet helpen om het proces dat we hebben doorlopen visueel uit te leggen.

Punt B

Punt B heeft coördinaten van (1,0,0,5).

Laten we opnieuw beginnen met de interpolatie van de X-as (hoewel je gemakkelijk eerst met Y zou kunnen beginnen als je dat zou willen!

Als we de X-as interpoleren over de bovenkant, moeten we 1,0 (100%) van de weg van 7 naar 0 gaan. U kunt het antwoord vast wel raden, maar hier wordt het berekend:
7 + (0-7) * 1,0 = 0

Op dezelfde manier doen we de X-as interpolatie over de onderkant. We moeten 1,0 (100%) van de weg van 3 naar 5 gaan.
3 + (5-3) * 1,0 = 5

Daarna komt de interpolatie van de Y-as. We moeten 0,5 (50%) van de weg van 5 naar 0.
5 + (0-5) * 0,5 = 2,5

Daar gaan we, de waarde in punt B is 2,5. Dat zou ook duidelijk moeten zijn als je naar het diagram kijkt. Het is in feite 1d lineaire interpolatie tussen 5 en 0, en ligt daar halverwege, dus intuïtief zou het antwoord 2,5 logisch moeten zijn.

Punt C

Punt C heeft een coördinaat van (0,8,0,2).

Opnieuw doen we de interpolatie van de X-as over de bovenkant van het vak. We moeten 0,8 (80%) van de weg van 7 naar 0 gaan.
7 + (0-7) * 0,8 = 1,4

Dan moeten we de x-as interpolatie doen over de bodem van het vak. We moeten 0,8 (80%) van de weg van 3 naar 5 gaan.
3 + (5-3) * 0,8 = 4,6

Ten slotte, de y-as interpolatie. We moeten 0,2 (20%) gaan van 4,6 naar 1,4.
4,6 + (1,4-4,6) * 0,2 = 3,96

De waarde van punt C is 3.96

Bilineaire filtering

Terwijl bilineaire interpolatie nuttig is als je een raster van data hebt waar je waarden binnen wilt interpoleren (zoals een hoogte veld dat terrein representeert?!), waar dit echt schittert in game ontwikkeling is in bilineaire textuur filtering.

Beginsel, wanneer je een textuur coördinaat hebt dat niet perfect in lijn is met het centrum van een pixel in de textuur (omdat er een rest is), gebruikt het het fractionele deel van de coördinaat binnen die pixel om bilineaire interpolatie te doen tussen de 4 betrokken pixels om uit te komen op de uiteindelijke pixelkleur. Het doet bilineaire interpolatie op elk van de kanalen: Rood, Groen, Blauw en Alfa.

Het eindresultaat is behoorlijk goed! Bekijk de afbeelding hieronder om het in actie te zien op een textuur waar we te ver op zijn ingezoomd. De linkerkant gebruikt bilineaire filtering, terwijl de rechterkant dat niet doet, en je gewoon de dichtstbijzijnde pixel laat zien.

Dientengevolge moet bilineaire texture filtering 4 pixel lezen om ertussen te kunnen interpoleren, in plaats van een enkele pixel te lezen zoals wanneer je nearest pixel sampling doet. Meer pixellezingen = meer overhead, en niet zo goedkoop (computationeel) om te gebruiken.

Links

Voor sommige mensen die dit lezen, is deze info vrij basaal en je vraagt je misschien af waarom ik de moeite nam om er over te schrijven. Kijk naar de volgende post voor iets bizar met betrekking tot bilineaire filtering. Dit was nodig als opstapje naar het volgende wat ik jullie wil laten zien 😛

Wikipedia: Lineaire Interpolatie

Wikipedia: Bilineaire Interpolatie

Wikipedia: Bilinear Filtering

The Dark Side of Bilinear Filtering

Kijk ook eens naar deze links voor wat diepere info over enkele tekortkomingen (en enkele workarounds) van hardware-gebaseerde bilineaire sampling:
iq: hardware interpolatie
iq: verbeterde textuur interpolatie