9.5 – Identificeren van invloedrijke gegevenspunten

In dit hoofdstuk leren we de volgende twee maatstaven voor het identificeren van invloedrijke gegevenspunten:

• Difference in Fits (DFFITS)
• Cook’s Distances

Het basisidee achter elk van deze maatstaven is hetzelfde, namelijk de waarnemingen één voor één te verwijderen, waarbij het regressiemodel telkens opnieuw wordt aangepast aan de resterende n-1 waarnemingen. Vervolgens vergelijken wij de resultaten met alle n waarnemingen met de resultaten waarbij de i-de waarneming is verwijderd om te zien hoeveel invloed de waarneming op de analyse heeft. Op die manier kunnen we de mogelijke invloed van elk gegevenspunt op de regressieanalyse beoordelen.

Verschil in fit (DFFITS)

Het verschil in fit voor waarneming i, aangeduid met DFFITSi, wordt gedefinieerd als:

Zoals u ziet, meet de teller het verschil in de voorspelde respons die wordt verkregen wanneer het i-de gegevenspunt wel en het i-de gegevenspunt niet in de analyse wordt opgenomen. De noemer is de geschatte standaardafwijking van het verschil in de voorspelde responsen. Het verschil in fit kwantificeert derhalve het aantal standaarddeviaties dat de passende waarde verandert wanneer het ide gegevenspunt wordt weggelaten.

Een waarneming wordt invloedrijk geacht indien de absolute waarde van haar DFFITS-waarde groter is dan:

waarbij, zoals altijd, n = het aantal waarnemingen en k = het aantal voorspellingstermen (d.w.z. het aantal regressieparameters exclusief het intercept). Het is belangrijk voor ogen te houden dat dit geen harde regel is, maar slechts een leidraad! Het is niet moeilijk te vinden dat verschillende auteurs een iets andere leidraad gebruiken. Daarom geef ik vaak de voorkeur aan een veel subjectievere richtlijn, bijvoorbeeld dat een gegevenspunt als invloedrijk wordt beschouwd als de absolute waarde van zijn DFFITS-waarde als een zere duim uitsteekt boven de andere DFFITS-waarden. Natuurlijk is dit een kwalitatief oordeel, misschien zoals het hoort, omdat uitschieters van nature subjectieve grootheden zijn.

Voorbeeld #2 (opnieuw). Laten we eens kijken naar het verschil in fits-maatstaf voor deze dataset (influence2.txt):

Regresseren we y op x en vragen we het verschil in passing op, dan krijgen we de volgende software-uitvoer:

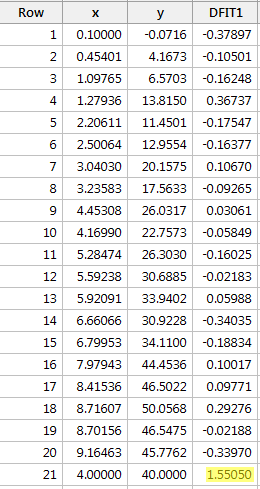
Gebaseerd op de hierboven gedefinieerde objectieve richtlijn, beschouwen we een gegevenspunt als invloedrijk als de absolute waarde van zijn DFFITS-waarde groter is dan:

Slechts één gegevenspunt – het rode – heeft een DFFITS-waarde waarvan de absolute waarde (1.55050) groter is dan 0,5.55050) groter is dan 0,82. Op basis van deze richtlijn beschouwen we het rode gegevenspunt dus als invloedrijk.

Voorbeeld #3 (opnieuw). Laten we eens kijken naar het verschil in past-maat voor deze gegevensverzameling (influence3.txt):

Regresseren we y op x en vragen we het verschil in passing op, dan krijgen we de volgende software-uitvoer:

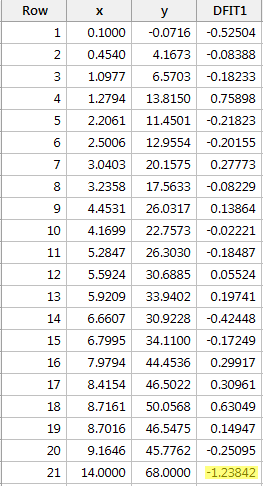
Gebaseerd op de hierboven gedefinieerde objectieve richtlijn, beschouwen we een gegevenspunt als invloedrijk als de absolute waarde van zijn DFFITS-waarde groter is dan:

Slechts één gegevenspunt – het rode – heeft een DFFITS-waarde waarvan de absolute waarde (1.23841) groter is dan 0,82. Daarom zouden we, op basis van deze richtlijn, het rode gegevenspunt als beïnvloedbaar beschouwen.

Toen we deze gegevensreeks in het begin van deze les bestudeerden, besloten we dat het rode gegevenspunt de regressieanalyse niet zo sterk beïnvloedde. Maar hier suggereert het verschil in pasmaat dat het wel degelijk invloedrijk is. Wat is hier aan de hand? Het komt erop neer dat alle metingen in deze les slechts hulpmiddelen zijn die mogelijk invloedrijke gegevenspunten markeren voor de data-analist. Uiteindelijk moet de analist de dataset twee keer analyseren – één keer met en één keer zonder de gemarkeerde gegevenspunten. Als de datapunten de uitkomst van de regressieanalyse significant veranderen, moet de onderzoeker de resultaten van beide analyses rapporteren.

In dit voorbeeld is het toevallig zo dat, als we de meer subjectieve richtlijn gebruiken van of de absolute waarde van de DFFITS-waarde eruit springt als een zere duim, we het rode datapunt waarschijnlijk niet als invloedrijk zullen beschouwen. De volgende grootste DFFITS-waarde (in absolute waarde) is immers 0,75898. Deze DFFITS-waarde verschilt niet veel van de DFFITS-waarde van ons “invloedrijke” gegevenspunt.

Voorbeeld #4 (opnieuw). Laten we eens kijken naar de difference in fits meting voor deze dataset (influence4.txt):

Regresseren we y op x en vragen we het verschil in passing op, dan krijgen we de volgende software-uitvoer:

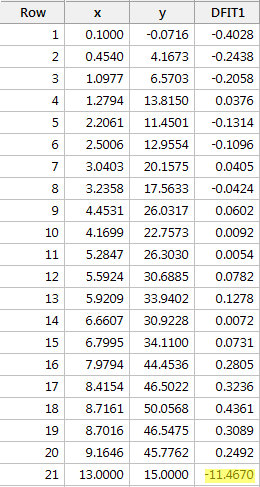
Gebaseerd op de hierboven gedefinieerde objectieve richtlijn, beschouwen we een gegevenspunt opnieuw als invloedrijk als de absolute waarde van zijn DFFITS-waarde groter is dan:

Wat denkt u? Zijn er DFFITS-waarden die er als een zere duim bovenuit steken? Errr – de DFFITS-waarde van het rode gegevenspunt (-11.4670 ) is zeker van een andere grootteorde dan alle andere. In dit geval zou er weinig twijfel over mogen bestaan dat het rode gegevenspunt invloedrijk is!

Cook’s Distance

Hier even tussen springen, Cook’s afstandsmaat, Di genoemd, is gedefinieerd als:

Het ziet er een beetje rommelig uit, maar het belangrijkste om te herkennen is dat Cook’s Di afhangt van zowel het residu, ei (in de eerste term), als het hefboomeffect, hii (in de tweede term). Dat wil zeggen dat zowel de x-waarde als de y-waarde van het gegevenspunt een rol spelen bij de berekening van Cook’s afstand.

In het kort:

• Di vat rechtstreeks samen hoeveel alle gepaste waarden veranderen wanneer de i-de waarneming wordt geschrapt.
• Een gegevenspunt met een grote Di geeft aan dat het gegevenspunt een sterke invloed heeft op de passende waarden.

Laten we eens onderzoeken wat die eerste bewering precies betekent in de context van enkele van onze voorbeelden.

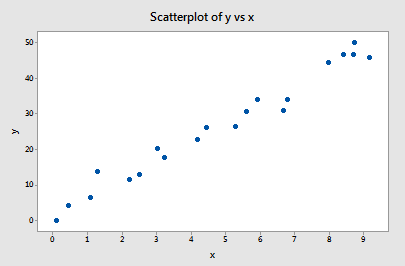
Voorbeeld #1 (opnieuw). U herinnert zich wellicht dat de plot van deze gegevens (influence1.txt) suggereert dat er geen uitschieters of invloedrijke gegevenspunten voor dit voorbeeld zijn:

Als we y op x regresseren met alle n = 20 gegevenspunten, stellen we vast dat de geschatte interceptcoëfficiënt b0 = 1,732 en de geschatte hellingcoëfficiënt b1 = 5,117. Als we het eerste gegevenspunt uit de gegevensreeks schrappen en y op x regresseren met de resterende n = 19 gegevenspunten, stellen we vast dat de geschatte interceptcoëfficiënt b0 = 1,732 en de geschatte hellingscoëfficiënt b1 = 5,1169. Zoals we hopen en verwachten, veranderen de schattingen niet veel wanneer we dat ene gegevenspunt weglaten. Als we verdergaan met dit proces, waarbij elk gegevenspunt een voor een wordt verwijderd, en de resulterende geschatte hellingen (b1) worden uitgezet tegen de geschatte intercepten (b0), krijgen we:

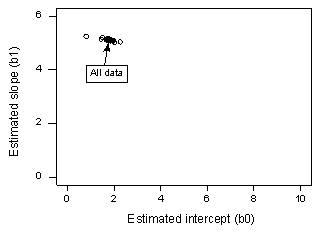
De vaste zwarte punt stelt de geschatte coëfficiënten voor op basis van alle n = 20 gegevenspunten. De open cirkels stellen elk van de geschatte coëfficiënten voor die worden verkregen door elk gegevenspunt één voor één te schrappen. Zoals u kunt zien, zijn de geschatte coëfficiënten allemaal samengebundeld, ongeacht welk gegevenspunt wordt verwijderd. Dit wijst erop dat geen enkel gegevenspunt de geschatte regressiefunctie of, op zijn beurt, de passende waarden overmatig beïnvloedt. In dit geval zou men verwachten dat alle Cook’s afstandsmaten, Di, klein zijn.

Voorbeeld #4 (opnieuw). U herinnert zich wellicht dat de plot van deze gegevens (influence4.txt) suggereert dat één gegevenspunt invloedrijk is en een uitbijter voor dit voorbeeld:

Als we y op x regresseren met alle n = 21 gegevenspunten, stellen we vast dat de geschatte interceptcoëfficiënt b0 = 8,51 en de geschatte hellingscoëfficiënt b1 = 3,32. Als we het rode gegevenspunt uit de dataset verwijderen en y op x regresseren met de resterende n = 20 gegevenspunten, stellen we vast dat de geschatte interceptcoëfficiënt b0 = 1,732 en de geschatte hellingscoëfficiënt b1 = 5,1169. De schattingen veranderen aanzienlijk na verwijdering van het ene gegevenspunt. Als we doorgaan met dit proces, waarbij elk gegevenspunt een voor een wordt verwijderd, en de resulterende geschatte hellingen (b1) tegen de geschatte intercepten (b0) worden uitgezet, krijgen we:

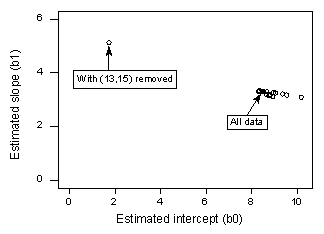
Ook hier stelt de vaste zwarte punt de geschatte coëfficiënten voor op basis van alle n = 21 gegevenspunten. De open cirkels stellen elk van de geschatte coëfficiënten voor die worden verkregen door elk gegevenspunt één voor één te schrappen. Zoals u kunt zien, zijn de geschatte coëfficiënten, met uitzondering van het rode gegevenspunt (x = 13, y = 15), allemaal samengebundeld, ongeacht welk gegevenspunt wordt verwijderd. Dit suggereert dat het rode gegevenspunt het enige gegevenspunt is dat de geschatte regressiefunctie en, op zijn beurt, de passende waarden overmatig beïnvloedt. In dit geval zou men verwachten dat de Cook’s afstandsmaat, Di, voor het rode gegevenspunt groot is en de Cook’s afstandsmaat, Di, voor de overige gegevenspunten klein.

Het gebruik van Cook’s afstandsmaat. Het mooie van bovenstaande voorbeelden is de mogelijkheid om met eenvoudige plots te zien wat er aan de hand is. Helaas kunnen we ons in het geval van meervoudige regressie niet verlaten op eenvoudige plots. In plaats daarvan moeten we ons baseren op richtlijnen om te bepalen wanneer een Cook’s afstandsmaat groot genoeg is om een gegevenspunt als invloedrijk te beschouwen.

Hierbij de meest gebruikte richtlijnen:

• Als Di groter is dan 0,5, dan is het i-de gegevenspunt het waard om verder te worden onderzocht omdat het invloedrijk kan zijn.
• Als Di groter is dan 1, dan is het i-de gegevenspunt zeer waarschijnlijk invloedrijk.
• Of, als Di als een zere duim uitsteekt boven de andere Di waarden, dan is het vrijwel zeker invloedrijk.

Voorbeeld #2 (opnieuw). Laten we eens kijken naar de Cook’s afstandsmaat voor deze gegevensverzameling (influence2.txt):

Regresseren we y op x en vragen we de Cook’s afstandsmaat op, dan krijgen we de volgende software-uitvoer:

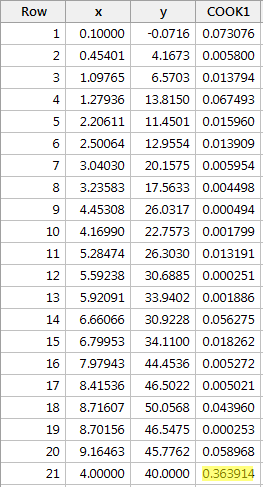
De Cook’s afstandsmaat voor het rode gegevenspunt (0,363914) springt er een beetje uit vergeleken met de andere Cook’s afstandsmaatstaven. Toch is de Cook’s afstandsmeting voor het rode gegevenspunt kleiner dan 0,5. Daarom zouden we, op basis van de Cook’s afstandsmaat, het rode gegevenspunt niet classificeren als invloedrijk.

Voorbeeld #3 (opnieuw). Laten we eens kijken naar de Cook’s afstandsmaat voor deze gegevensverzameling (influence3.txt):

Regresseren we y op x en vragen we de Cook’s afstandsmaat op, dan krijgen we de volgende software-uitvoer:

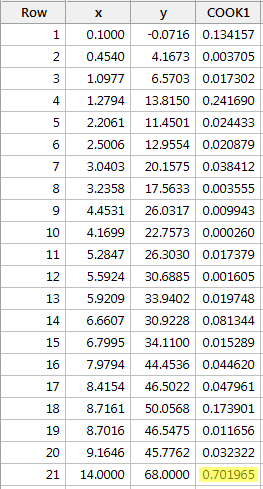
De Cook’s afstandsmaat voor het rode gegevenspunt (0,701965) springt er een beetje uit vergeleken met de andere Cook’s afstandsmaatstaven. Toch is de Cook’s afstandsmeting voor het rode gegevenspunt groter dan 0,5 maar kleiner dan 1. Daarom zouden we, gebaseerd op de Cook’s afstandsmeting, het rode gegevenspunt misschien verder onderzoeken maar niet noodzakelijk als invloedrijk classificeren.

Voorbeeld #4 (opnieuw). Laten we eens kijken naar de Cook’s afstandsmaat voor deze gegevensverzameling (influence4.txt):

Regresseren we y op x en vragen we de Cook’s afstandsmaat op, dan krijgen we de volgende software-uitvoer:

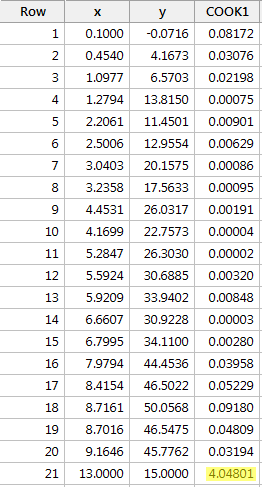
In dit geval springt de Cook’s afstandsmaat voor het rode gegevenspunt (4.04801) er substantieel uit vergeleken met die voor het rode gegevenspunt (4.04801).04801) er aanzienlijk uit vergeleken met de andere Cook’s afstandsmaten. Bovendien is de Cook’s afstandsmeting voor het rode gegevenspunt groter dan 1. Op basis van de Cook’s afstandsmeting – en dat is niet verwonderlijk – classificeren we het rode gegevenspunt daarom als invloedrijk.

Een alternatieve methode voor het interpreteren van Cook’s afstand die soms wordt gebruikt, is de maat te relateren aan de F(k+1, n-k-1) verdeling en de bijbehorende percentielwaarde te vinden. Als dit percentiel lager is dan ongeveer 10 of 20 procent, dan heeft het geval weinig invloed op de aangepaste waarden. Anderzijds, als het in de buurt van 50 procent of zelfs hoger ligt, dan heeft het geval een grote invloed. (Alles “ertussenin” is meer dubbelzinnig.)