Mathematics for the Liberal Arts
Learning Outcomes
- Bestimmen und identifizieren Sie Selbstähnlichkeit in geometrischen Formen, Pflanzen, und geologischen Formationen
- Generieren Sie eine fraktale Form anhand eines Initiators und eines Generators
- Skalieren Sie ein geometrisches Objekt mit einem bestimmten Skalierungsfaktor unter Verwendung der Skalierungsdimensionsbeziehung
- Bestimmen Sie die fraktale Dimension eines fraktalen Objekts
Neben der visuellen Selbstähnlichkeit weisen Fraktale weitere interessante Eigenschaften auf. Man beachte zum Beispiel, dass bei jedem Schritt der Iteration der Sierpinski-Dichtung ein Viertel der verbleibenden Fläche entfernt wird. Wenn dieser Prozess unbegrenzt fortgesetzt wird, würde am Ende im Wesentlichen die gesamte Fläche entfernt, was bedeutet, dass wir mit einer zweidimensionalen Fläche begonnen haben und am Ende etwas haben, das kleiner ist als diese, aber anscheinend mehr als eine eindimensionale Linie.
Um diese Idee zu erforschen, müssen wir über Dimensionen sprechen. Etwas wie eine Linie ist 1-dimensional; sie hat nur eine Länge. Jede Kurve ist 1-dimensional. Dinge wie Kästen und Kreise sind 2-dimensional, da sie eine Länge und eine Breite haben, die eine Fläche beschreiben. Objekte wie Kästchen und Zylinder haben Länge, Breite und Höhe, die ein Volumen beschreiben, und sind 3-dimensional.
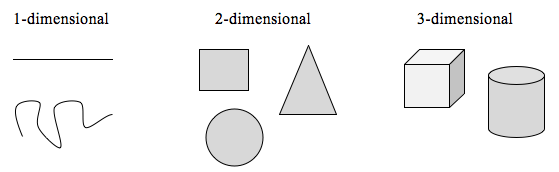
Für die Skalierung von Objekten gelten bestimmte Regeln, die sich auf ihre Dimension beziehen.
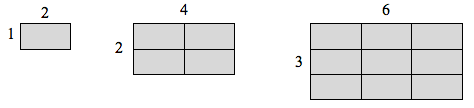
Wenn ich eine Linie der Länge 1 hätte und ihre Länge um 2 skalieren wollte, bräuchte ich zwei Kopien der ursprünglichen Linie. Hätte ich eine Linie der Länge 1 und wollte ihre Länge um 3 skalieren, bräuchte ich drei Kopien des Originals.
Wenn ich ein Rechteck mit der Länge 2 und der Höhe 1 hätte und seine Länge und Breite um 2 skalieren wollte, bräuchte ich vier Kopien des ursprünglichen Rechtecks. Wenn ich die Länge und die Breite um 3 skalieren wollte, bräuchte ich neun Kopien des ursprünglichen Rechtecks.
Wenn ich einen Würfel mit der Seitenlänge 1 hätte und seine Länge und Breite um 2 skalieren wollte, bräuchte ich acht Kopien des ursprünglichen Würfels. Wenn ich die Länge und Breite mit 3 skalieren wollte, bräuchte ich 27 Kopien des ursprünglichen Würfels.
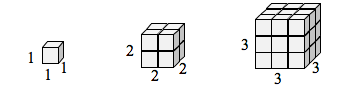
Beachte, dass im eindimensionalen Fall die benötigten Kopien gleich dem Maßstab sind.
Im zweidimensionalen Fall sind die benötigten Kopien gleich dem Maßstab^{2}.
Im dreidimensionalen Fall sind die benötigten Kopien gleich dem Maßstab^{3}.
Aus diesen Beispielen können wir ein Muster ableiten.
Skalierung-Dimension-Beziehung
Um eine D-dimensionale Form um einen Skalierungsfaktor S zu skalieren, ist die Anzahl der benötigten Kopien C der ursprünglichen Form gegeben durch:
\text{Kopien}=\text{Skala}^{\text{Dimension}}, oder C=S^{D}
Beispiel
Benutzen Sie die Skalierung-Dimension-Beziehung, um die Dimension der Sierpinski-Dichtung zu bestimmen.
Angenommen, die ursprüngliche Dichtung hat die Seitenlänge 1. Die dargestellte größere Dichtung ist doppelt so breit und doppelt so hoch, wurde also um den Faktor 2 skaliert.
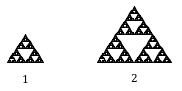
Beachte, dass zur Konstruktion der größeren Dichtung drei Kopien der ursprünglichen Dichtung benötigt werden.
Wenn man die Skalierungs-Dimensions-Relation C=S^{D} verwendet, erhält man die Gleichung 3=2^{D}.
Da 2^{1}=2 und 2^{2}=4 ist, können wir sofort sehen, dass D irgendwo zwischen 1 und 2 liegt; die Dichtung ist mehr als eine 1-dimensionale Form, aber wir haben so viel Fläche weggenommen, dass sie jetzt weniger als 2-dimensional ist.
Die Lösung der Gleichung 3=2^{D} erfordert Logarithmen. Wenn du dich früher mit Logarithmen beschäftigt hast, erinnerst du dich vielleicht daran, wie man diese Gleichung löst (wenn nicht, geh einfach zum folgenden Kasten und benutze diese Formel mit der Logarithmentaste auf einem Taschenrechner):
Nimm den Logarithmus beider Seiten.
3={{2}^{D}}
Benutze die Exponenteneigenschaft von Logarithmen.
\log(3)=\log\left({{2}^{D}}\right)
Dividiere durch log(2).
\log(3)=D\log\left(2\right)
Die Abmessung der Dichtung beträgt etwa 1,585.
D=\frac{\log\left(3\right)}{\log(2)}approx1.585
Skalierungs-Dimensions-Relation, um die Dimension zu finden
Um die Dimension D eines Fraktals zu finden, bestimmen Sie den Skalierungsfaktor S und die Anzahl der benötigten Kopien C der ursprünglichen Form, Verwenden Sie dann die Formel
D=\frac{\log\left(C\right)}{\log(S)}
Versuchen Sie es
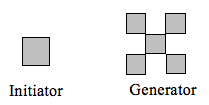
Bestimmen Sie die fraktale Dimension des Fraktals, das mit dem Initiator und dem Generator erzeugt wurde.
Im folgenden Video wird anhand eines praktischen Beispiels gezeigt, wie man die Dimension der Sierpinski-Dichtung bestimmt

Leave a Reply