Mathematics for the Liberal Arts
Learning Outcomes
- 幾何図形、植物における自己相似性を定義し識別することができる。
- 開始点と発生点が与えられたら、フラクタル図形を生成する
- スケーリング次元の関係を使って、特定のスケーリングファクターで幾何学的オブジェクトをスケールする
- フラクタル オブジェクトのフラクタル次元を決める
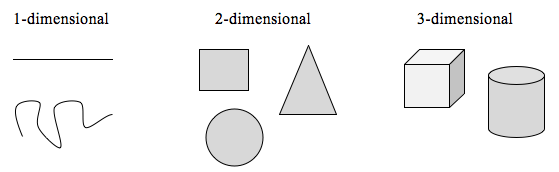
ビジュアルな自己相似性に加えて、フラクタルには他の興味深い特性もあります。 例えば、シェルピンスキーのガスケットの反復の各ステップは残りの面積の1/4を削除していることに注目してください。 このプロセスを無限に続けると、実質的にすべての領域を削除することになります。つまり、2 次元の領域から始めて、どうにかそれ以下の、しかし一見すると 1 次元の線以上のものができあがります。 線のようなものは 1 次元です; それは長さだけを持っています。 どんな曲線も 1 次元です。 箱や円のようなものは、長さと幅があり、面積を表すので、2次元です。 箱や円筒のようなものは長さ、幅、高さを持ち、体積を表すので3次元である。
オブジェクトの拡大縮小には、その寸法に関連した一定のルールが適用される。
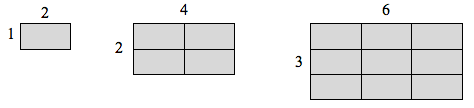
長さ 1 の線があり、その長さを 2 倍にしたい場合、元の線のコピーが 2 つ必要になる。
長さ 2、高さ 1 の長方形があり、その長さと幅を 2 倍にしたい場合、元の長方形のコピーが 4 つ必要です。
長さ 1 の辺を持つ立方体の箱があり、その長さと幅を 2 倍にしたい場合、元の立方体のコピーが 8 個必要になります。
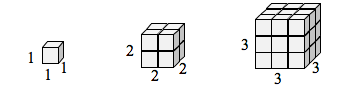
1次元の場合、必要なコピー=スケールであることに注意。
2次元の場合、必要なコピー=スケール^{2}。
スケーリング-次元の関係
D次元の形状をスケーリング係数Sでスケーリングするには、元の形状の必要なコピー数Cは次で与えられるでしょう。
Copies}=Scale}^{Dimension}, or C=S^{D}
例
Sierpinski gasketの寸法を決定するためにスケーリング-寸法の関係を使用します。
元のガスケットの辺の長さを1と定義すると、表示されている大きなガスケットは幅と高さが2倍なので、2倍に拡大されている。
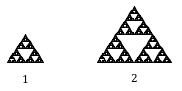
大きなガスケットを作るには、元のガスケットのコピーが3つ必要なことに注意してください。
拡大・縮小の関係 C=S^{D} を使って、3=2^{D} という方程式が得られます。
2^{1}=2、2^{2}=4なので、Dは1と2の間のどこかにあることがすぐに分かります。ガスケットは1次元以上の形状ですが、面積を大きく取ったので2次元以下になってしまいました。
方程式3=2^{D}を解くには対数が必要です。 もし以前に対数を勉強していれば、この方程式の解き方を思い出すかもしれません(そうでなければ、下のボックスまで飛ばして、電卓のlogキーでその公式を使ってください):
両辺の対数をとります。
3={{2}^{D}}
対数の指数特性を使用します。
log(3)=⑯logleft({{2}^{D}})
log(2) で割ると、次のようになります。
↩log(3)=D┣log(2right)
The dimension of gasket is about 1.585.
D=┣log(3right)}{PROX1.2}
Scaling-Dimension Relation, to find Dimension
フラクタルの次元Dを求めるには、スケーリング係数Sと原形の必要コピー枚数Cを決めます。 次に式
D=Centa{logleft(Centaright)}{log(S)}
Try It
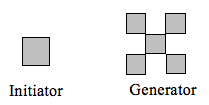
開始器と発生器を用いて生成したフラクタル次元を決定してください。
In the following video, we present a working example of how to determine the dimension of the Sierpinski gasket
…

Leave a Reply