Gram-Schmidt process
by Marco Taboga, PhD
Gram-Schmidt process(または手続き)は、線形独立なベクトルの集合を、元の集合によって広げられた同じ空間に渡る直交ベクトルの集合に変換できる一連の操作のことである。

予備知識
ここで、グラム・シュミット過程を理解する上で欠かせないいくつかの概念をおさらいしておきましょう。
2つのベクトル と
と は、それらの内積が0に等しい場合にのみ直交すると言われていること、つまり
は、それらの内積が0に等しい場合にのみ直交すると言われていること、つまり
内積が与えられると、次のようにベクトル のノルム(長さ)を定義できることを覚えておいてください。
のノルム(長さ)を定義できることを覚えておいてください。
ベクトルの集合は、その要素が単位ノルムを持ち、互いに直交している場合にのみ、直交性と呼ばれます。 すなわち、 個のベクトルの集合
個のベクトルの集合 は、
は、
以下の場合にのみ、直交正規集合のベクトルが線形独立であることを証明した。
直交集合への射影
グラム・シュミット法では次の命題を繰り返し用いるが、これはすべてのベクトルが1)直交集合への射影と2)与えられた直交集合に直交する残差に分解できることを示す。
命題  は内積
は内積 を備えたベクトル空間とする。 また、
を備えたベクトル空間とする。 また、 を正規直交集合とする。 任意の
を正規直交集合とする。 任意の に対して、
に対して、 ここで
ここで は
は に対して、任意の
に対して、任意の
定義 すると、各
すると、各 に対して、
に対して、 ここで、以下のようになる。 ステップ
ここで、以下のようになる。 ステップ と
と では、内積がその第1引数に線形であることを利用している。 ステップ
では、内積がその第1引数に線形であることを利用している。 ステップ では、正則集合を扱っているので、
では、正則集合を扱っているので、 ならば
ならば という事実を使い、ステップ
という事実を使い、ステップ では、
では、 のノルムは1に等しいという事実を使いました。 したがって、上で定義した
のノルムは1に等しいという事実を使いました。 したがって、上で定義した は、直交集合のすべての要素に直交しており、命題が証明される。
は、直交集合のすべての要素に直交しており、命題が証明される。
項 は
は の直交集合
の直交集合 への線形射影と呼ばれ、項
への線形射影と呼ばれ、項 は線形射影の残差と呼ばれています。
は線形射影の残差と呼ばれています。
正規化
また、グラム・シュミット処理で繰り返し使うことになる、おそらく明白な事実は、任意の非ゼロベクトルを取ってそのノルムで割ると、割った結果は単位ノルムを持つ新しいベクトルになることである。
つまり、 ならば、ノルムの確定性により、
ならば、ノルムの確定性により、
結果として、 を定義でき、ノルムの正値性と絶対同値性により、以下のようになる。 6451>
を定義でき、ノルムの正値性と絶対同値性により、以下のようになる。 6451>
手順の概要
さて、ベクトルの正規化方法と直交集合への射影と残差への分解方法がわかったので、グラム・シュミット手順を説明することにします。
ここではその概要を説明し、その後、命題として正式に表現し、技術的な詳細は命題の証明ですべて説明します。
ここでは概要です。 線形独立なベクトルの集合
線形独立なベクトルの集合 が与えられています。
が与えられています。
処理を始めるにあたり、最初のベクトルを正規化する、つまり
第二段階として、 を
を :
: に射影する、ここで
に射影する、ここで は射影の残差である。
は射影の残差である。
次に残差を正規化する:
出発ベクトルは線形独立なので、 (正規化ができるように)後で証明することにする。
(正規化ができるように)後で証明することにする。
こうして得られた2つのベクトル と
と は、直交正規分布であることがわかる。
は、直交正規分布であることがわかる。
第三段階として、 を
を と
と :
: に射影し、その残差を計算する
に射影し、その残差を計算する  。
。
そしてそれを正規化する: 最後の正規化残差を得るまでこの方法で進める。
最後の正規化残差を得るまでこの方法で進める。
プロセスの最後に、ベクトル は正規直交集合を形成する。なぜなら、
は正規直交集合を形成する。なぜなら、
-
それらは正規化の結果であり、結果として単位ノルムを持つ。
-
それぞれの
 は
は に直交するという特性を持つ残余から得られたものである。
に直交するという特性を持つ残余から得られたものである。
この概観を完成するために、 の線形スパンは
の線形スパンは の線形結合として書くことができるすべてのベクトルの集合であり、それは
の線形結合として書くことができるすべてのベクトルの集合であり、それは で示され、線形空間であることを覚えておこう。
で示され、線形空間であることを覚えておこう。
ベクトル は
は の線形独立結合なので、
の線形独立結合なので、 の線形結合として書ける任意のベクトルは
の線形結合として書ける任意のベクトルは の線形結合としても書くことができる。 したがって、2つのベクトル集合のスパンは一致する。
の線形結合としても書くことができる。 したがって、2つのベクトル集合のスパンは一致する。
Formal statement
我々はここでGram-Schmidt過程を命題として定式化し、その証明には手順のすべての技術的詳細が含まれている。
Proposition  は内積
は内積  が付いたベクタ空間とする。 また、
が付いたベクタ空間とする。 また、 を線形独立なベクトルとする。 このとき、任意の
を線形独立なベクトルとする。 このとき、任意の に対して
に対して となるような直交ベクトル集合
となるような直交ベクトル集合 が存在する。
が存在する。
証明は帰納法で、まず について命題が成り立つことを証明し、次に
について命題が成り立つことを証明し、次に について成り立つなら一般
について成り立つなら一般 についても真であることを証明します。
についても真であることを証明します。  のとき、ベクトル
のとき、ベクトル は単位ノルムを持ち、それだけで直交集合を構成する:他にベクトルはないので、直交条件は些細に満たされる。 集合
は単位ノルムを持ち、それだけで直交集合を構成する:他にベクトルはないので、直交条件は些細に満たされる。 集合 は
は のすべてのスカラー倍数の集合であり、それは
のすべてのスカラー倍数の集合であり、それは のスカラー倍数でもある(逆もまたしかりである)。 したがって、
のスカラー倍数でもある(逆もまたしかりである)。 したがって、 ここで、
ここで、 について命題が成立しているとする。 すると、
について命題が成立しているとする。 すると、 を
を :
: 上に投影することができ、ここで残差
上に投影することができ、ここで残差 は
は に直交していることがわかる。
に直交していることがわかる。  であるとする。 すると、
であるとする。 すると、 仮定により、
仮定により、 任意の
任意の に対して、
に対して、
 はスカラーであることが分かる。 したがって、
はスカラーであることが分かる。 したがって、 つまり、
つまり、 という仮定から、
という仮定から、 は
は の線形結合であるという結論が導き出される。 しかし、この命題の前提の1つは
の線形結合であるという結論が導き出される。 しかし、この命題の前提の1つは が線形独立であることなので、これは不可能である。 結果的に、
が線形独立であることなので、これは不可能である。 結果的に、 でなければならない。 そこで残差を正規化し、単位ノルムを持つベクトル
でなければならない。 そこで残差を正規化し、単位ノルムを持つベクトル を定義すればよい。 すでに
を定義すればよい。 すでに が
が に直交していることが分かっています。 このことから、
に直交していることが分かっています。 このことから、 も
も に直交していることがわかります。 よって、
に直交していることがわかります。 よって、 は直交集合である。 さて、
は直交集合である。 さて、 として書ける任意のベクトル
として書ける任意のベクトル (
( はスカラー)をとります。 仮定により、
はスカラー)をとります。 仮定により、 式(2)は
式(2)は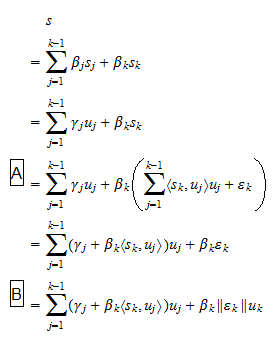 式(2370>はスカラー)とも書けるので、ステップ
式(2370>はスカラー)とも書けるので、ステップ では式(1)、ステップ
では式(1)、ステップ では
では の定義を使っていることになります。 したがって、
の定義を使っていることになります。 したがって、 の線形結合として書けるすべてのベクトルは、
の線形結合として書けるすべてのベクトルは、 の線形結合としても書けることが証明されました。 仮定(3)により、完全に類似した方法で逆を証明することができます:
の線形結合としても書けることが証明されました。 仮定(3)により、完全に類似した方法で逆を証明することができます: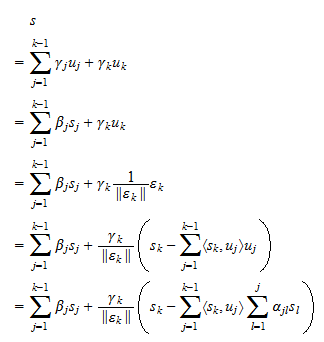 言い換えれば、
言い換えれば、 のすべての線形結合は
のすべての線形結合は の線形結合でもあるのです。 これは
の線形結合でもあるのです。 これは を証明し、証明を終える。
を証明し、証明を終える。
Every inner product space has an orthonormal basis
以下の命題はGram-Schmidt processの重要な結果を示す。
命題  が内積
が内積  を備えたベクトル空間とする。
を備えたベクトル空間とする。  が有限次元
が有限次元 であるならば、
であるならば、 に直交基底
に直交基底 が存在する。
が存在する。
 は有限次元なので、
は有限次元なので、 には
には ベクトル
ベクトル からなる基底が少なくとも1つ存在する。 この基底にGram-Schmidt法を適用して、直交集合
からなる基底が少なくとも1つ存在する。 この基底にGram-Schmidt法を適用して、直交集合 を得ることができる。
を得ることができる。  は基底であるから、
は基底であるから、 にまたがる。 したがって、
にまたがる。 したがって、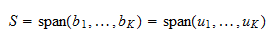 したがって、
したがって、 は
は の正則基底です。
の正則基底です。
解いた練習問題
以下に、練習問題の解説を掲載します。
練習問題1
実数エントリを持つすべての ベクトルの空間
ベクトルの空間 と内積
と内積 ここで
ここで  と
と  は
は の転置と考えよ。 ベクトル
の転置と考えよ。 ベクトル
 を正規化すると定義される。
を正規化すると定義される。
 のノルムは
のノルムは したがって。
したがって。  の正規化は
の正規化は 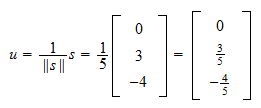
練習問題2
実数エントリを持つすべての  ベクトルの空間
ベクトルの空間  と内積
と内積  where
where  を考えてみましょう. 線形独立な2つのベクトル
を考えてみましょう. 線形独立な2つのベクトル
Gram-Schmidt法により直交集合に変換することを考えよう。
 のノルムは
のノルムは であるから。 最初の正則ベクトルは
であるから。 最初の正則ベクトルは
 と
と の内積は
の内積は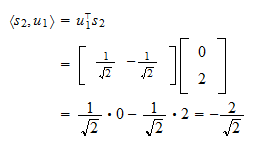
 の
の への投影は
への投影は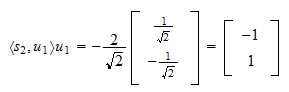 投影残差は
投影残差は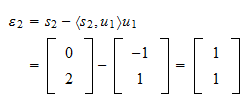 そのノルムは
そのノルムは そして正規化残差は
そして正規化残差は このようにして、は、
このようにして、は、 となります。 探していた正則集合は
となります。 探していた正則集合は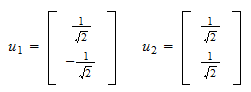
引用方法
として引用してください。
Taboga, Marco (2017). “Gram-Schmidt process”, 行列代数学講義. https://www.statlect.com/matrix-algebra/Gram-Schmidt-process.
Leave a Reply