Friedman Test in SPSS Statistics
SPSS Statistics
SPSS Statistics Output for the Friedman Test
SPSS Statistics will generate either two or three tables, depending on whether you selected to have descriptives and/or quartiles generated in addition to running the Friedman test.SPSS Statistics は、フリードマンのテストを実行すると、2 つの表または 3 つの表を生成します。
Descriptive Statistics Table
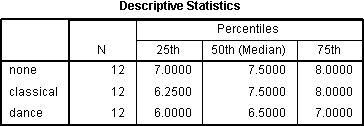
Quartiles オプションを選択した場合、Descriptive Statistics テーブルが生成されます:
Published with written permission from SPSS Statistics, IBM Corporation.
This is a very useful table because it can be used to present descriptive statistics in your results section for each of the time points or conditions (depending on your study design) for your dependent variable.これは結果セクションに記述統計学を示すのに使用することができるので、非常に便利な表です。 この有用性は、後の「アウトプットの報告」セクションで紹介します。
Ranks Table
Ranksテーブルは、以下に示すように、関連する各グループの平均ランクを示します:

Published with written permission from SPSS Statistics, IBM Corporation.
Friedman testは関連グループ間の平均ランクを比較して、グループがどう違うかを示しており、そのために含まれている。
検定統計表
検定統計表は、フリードマン検定の実際の結果、および関連グループの平均順位間に全体的に統計的に有意な差があったかどうかを知らせます。 このガイドで使用される例では、テーブルは次のようになります:

Published with written permission from SPSS Statistics, IBM Corporation.
上の表は、検定統計量(χ2) 値(「カイ二乗」)、自由度(「df」)、有意水準(「Asymp. Sig. 」)、これだけあれば、Friedman検定の結果を報告することができます。 この例から、関連するグループの平均順位の間に、全体として統計的に有意な差があることがわかります。 Friedman 検定は、そのパラメトリック代わりのように、オムニバス検定であることに注意することが重要です; つまり、全体的な差があるかどうかを示しますが、特にどのグループが互いに異なるかを特定することはありません。 これを行うには、ポストホック検定を実行する必要がありますが、これについては次のセクション以降で説明します。
SPSS Statistics
フリードマン検定の出力を報告する(ポストホック検定なし)
次のようにフリードマン検定の結果を報告できます:
- General
There was statistically significant difference in perceived effort according to which type of music was listened while running, χ2(2) = 7.2pt.600, p = 0.022.
関連する各グループの中央値も含めることができます。 ただし、この段階では、関連集団のどこかに差があることがわかるだけで、その差がどこにあるのかは正確にはわかりません。
ポストホックテスト
差異が実際にどこにあるかを調べるには、関連群の異なる組み合わせで別々のWilcoxon signed-rank 検定を実行する必要があることを覚えておいてください。 つまり、この例では、次の組み合わせを比較します:
- None to Classical.
- None to Dance.
- Classical to Dance.
多重比較をしているので、本来有意ではない結果を有意と判定する可能性(タイプIエラー)を高くしていることから、ウィルコクソン検定から得た結果にボンフェローニ調整を使用しなければいけません。 幸運なことに、ボンフェローニ調整はとても簡単に計算できます。最初に使っていた有意水準(この場合、0.05)を取り、それを実行するテストの数で割るだけです。 つまり、この例では、新しい有意水準は0.05/3 = 0.017となります。
この例の結果に対して、これらの検定(ウィルコクソンの符号順位検定ガイドで方法を確認)を実行すると、次の結果が得られます:

Published with written permission from SPSS Statistics, IBM Corporation.以下、「SPSS統計局」です。
この表は、私たちのそれぞれの組み合わせに対するWilcoxon signed-rank testの出力を示しています。 注意すべきは、有意水準が多重比較を補償するためにSPSS Statisticsで調整されていないことです – SPSS Statisticsで生成された有意水準とあなたが計算したボンフェローニ調整された有意水準とを手動で比較する必要があります。 p < 0.017の有意水準で、音楽なしとダンス(ダンスなし、p = 0.008)の間の知覚的努力だけが統計的に有意に異なっていることがわかります。
SPSS Statistics
フリードマン検定の結果を報告する(ポストホックテストあり)
Friedman test with post hoc tests resultsは以下のように報告できます:
- General
There was a statistically significant difference in perceived effort depending to which type of music listened while running, χ2(2) = 7.2ptips of music.600, p = 0.022. Wilcoxon符号順位検定によるポストホック解析を行い、ボンフェローニ補正を適用した結果、有意水準はp < 0.017に設定された。 音楽なし、クラシック、ダンスミュージックのランニングトライアルの知覚努力レベルの中央値(IQR)は、それぞれ7.5(7〜8)、7.5(6.25〜8)、6.5(6〜7)であった。 音楽なしとクラシック音楽のランニング試験(Z = -0.061, p = 0.952)、クラシック音楽とダンス音楽のランニング試験(Z = -1.811, p = 0.070)では、ダンスとクラシック音楽のランニング試験で全体の知覚努力が減少したにもかかわらず、有意差はなかった。 しかし、ダンス音楽と音楽なしの試行では、統計的に有意な努力の減少が見られた(Z = -2.636, p = 0.008)
Leave a Reply