9.5 – Identifying Influential Data Points

このセクションでは、影響力のあるデータポイントを識別するための以下の2つの尺度を学びます：

• Difference in Fits (DFFITS)
• Cook’s Distances

これらの各尺度の基本概念は同じです、つまり、一度にひとつずつ観測値を消し、そのたびに残りのn-1の観測値に回帰モデルを再フィットすることです。 そして、オブザベーションが分析にどれだけ影響するかを見るために、すべてのn個のオブザベーションを用いた結果とi番目のオブザベーションを削除した結果を比較します。

Difference in Fits (DFFITS)

オブザベーションiの適合の差（DFFITSiと表記）は、次のように定義されます：

見てわかるように、分子はi番目のデータ点が分析から含まれ除かれているときに得られる予測される反応の差を測定しています。 分母は予測される反応の差の推定標準偏差である。 したがって，適合の差は，i番目のデータポイントが省略されたときに，適合値が変化する標準偏差の数を定量化する． これはハード＆ファスト・ルールではなく、ガイドラインに過ぎないことを心に留めておくことが重要である! 著者によって微妙に異なるガイドラインを使用しているのを見つけるのは難しいことではありません。 したがって、私はより主観的なガイドライン、例えば、あるデータポイントのDFFITS値の絶対値が他のDFFITS値より突出している場合、そのデータポイントは影響力があると判断する、というようなガイドラインを好むことが多いです。 もちろん、これは定性的な判断ですが、外れ値はその性質上、主観的な量なので、おそらくそうあるべきでしょう。 このデータセット（influence2.）の適合度測定の差を確認してみましょう。txt):

y を x に回帰して difference in fits を要求すると、次のソフトウェア出力を得ることができます。

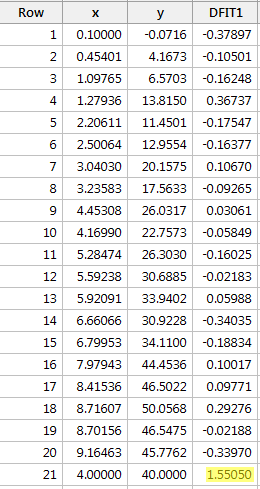
上で定義した客観的ガイドラインを使用し、そのDFFITS値の絶対値が以下の場合、データポイントは影響力があると見なします：

ただ一つのデータポイント – 赤いポイント – にはその絶対値（1.55050)が0.82より大きいデータポイントは1つだけである。 したがって、このガイドラインに基づけば、赤いデータポイントは影響力があると考えることができます。

例3（再び）。 このデータセット(influence3.)の適合度の差の指標を確認してみましょう。txt):

y を x に回帰して difference in fits を要求すると、次のソフトウェア出力を得ることができます。

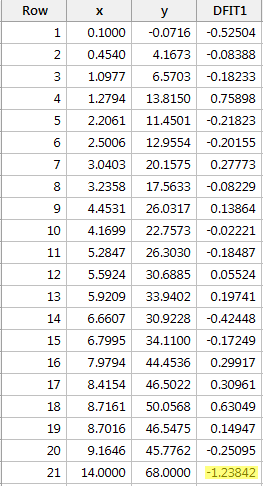
上で定義した客観的ガイドラインを使用し、そのDFFITS値の絶対値が以下の場合、データポイントは影響力があると見なします：

たった1つのデータポイント – 赤いポイント – その絶対値（1.23841)が0.82より大きい。 そのため、このガイドラインに基づけば、赤いデータ点は影響力があると考えられます。

このレッスンの最初にこのデータセットを調べたとき、赤いデータ点は回帰分析にそれほど影響を与えないと判断しています。 しかし、ここでは、適合度測定の差は、それが実際に影響力があることを示唆している。 何が起こっているのでしょうか？ それは、このレッスンのすべての測定は、データ分析者にとって潜在的に影響力のあるデータポイントを示すツールに過ぎないということを認識することです。 最終的には、分析者はデータセットを2回分析する必要があります。1回はフラグを立てたデータポイントを使い、もう1回はフラグを立てないデータポイントを使います。 もしそのデータポイントが回帰分析の結果を大きく変えるのであれば、研究者は両方の分析結果を報告すべきです。

ちなみに、この例では、DFFITS値の絶対値が親指のように突き出ているかというより主観的なガイドラインを使用すると、赤いデータポイントは影響力があるとはみなされない可能性があります。 なにしろ、次に大きいDFFITS値（絶対値）は0.75898なのだから。 このDFFITS値は、今回の「影響力のある」データポイントのDFFITS値と大差ありません。

例4（再び）。 このデータセット（influence4.）の適合度の差の指標を確認してみましょう。txt):

y を x に回帰し、適合度の差を要求すると、次のソフトウェア出力を得ることができます。

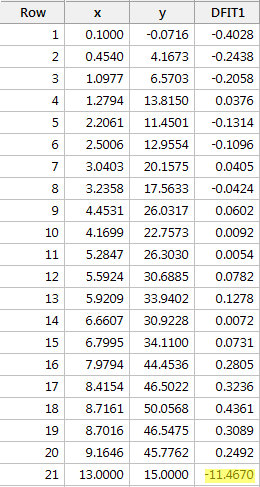
上で定義した客観的ガイドラインを使用して、その DFFITS 値の絶対値が次の値より大きい場合、再びデータ ポイントが影響力があると見なします：

どうでしょうか？ DFFITS値が突出しているものはないでしょうか？ えーと、赤いデータポイントのDFFITS値（-11.4670）は、確かに他のすべてのデータポイントと大きさが違いますね。 この場合、赤いデータポイントが影響力があることは間違いないでしょう！

Cook’s Distance

ここで、Cookの距離指標（Diと表記）は次のように定義されます：

少し面倒に見えますが、主に認識すべきことはCookのDiが第1項で残差eiと第2項でレバレッジhii両方に依存している、ということです。 つまり、データ点のx値とy値の両方がCookの距離の計算で役割を果たします。

つまり、

• Diはi番目の観測値を削除したときにすべての適合値がどのくらい変化するかを直接要約したものです。
• 大きな Di を持つデータ点は、そのデータ点がフィット値に強く影響することを示します。

いくつかの例のコンテキストで、最初の声明が正確に何を意味するかを調べてみましょう。 これらのデータのプロット (influence1.txt) が、この例には外れ値も影響力のあるデータ ポイントもないことを示唆していることを思い出すかもしれません:

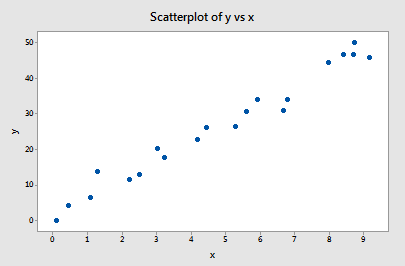
すべての n = 20 データ ポイントを使って y を x に回帰すると、推定インターセプト係数 b0 = 1.732 および推定スロープ係数 b1 = 5.117 と判定されました。 データセットから最初のデータポイントを削除し、残りのn = 19個のデータポイントを使用してyをxに回帰すると、推定切片係数b0 = 1.732、推定スロープ係数b1 = 5.1169と決定されます。 私たちが期待するように、1つのデータポイントを削除しても、推定値はそれほど変わりません。 このようにデータポイントを1つずつ削除していき、その結果の推定傾き（b1）と推定切片（b0）をプロットすると、次のようになります：

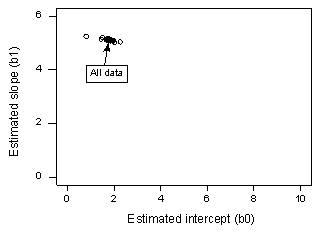
黒い実線はn=20個のデータポイントすべてに基づく推定係数を表します。 開いている円は、各データポイントを1つずつ削除したときに得られた各推定係数を表している。 このように、どのデータポイントを削除しても、推定係数がまとまっていることがわかる。 これは、どのデータポイントも推定された回帰関数、ひいてはフィット値に不当に影響を及ぼしていないことを示唆しています。 この場合、Cookの距離指標Diはすべて小さいことが予想されます。

例題4（再び）。 これらのデータのプロット（influence4.txt）が、この例では1つのデータ点が影響力があり、外れ値であることを示唆していることを思い出すかもしれません：

すべてのn = 21データ点を使ってxにyを回帰すると、推定切片係数b0 = 8.51、推定傾斜係数b1 = 3.32 だと判定されました。 もし、データセットから赤いデータ点を取り除き、残りのn=20個のデータ点を使ってyをxに回帰させると、推定切片係数b0=1.732、推定傾き係数b1=5.1169となることが判ります。 なんと、1つのデータポイントを削除しただけで、推定値が大きく変化しています。 このようにデータポイントを1つずつ削除していき、その結果の推定傾き（b1）と推定切片（b0）をプロットすると、

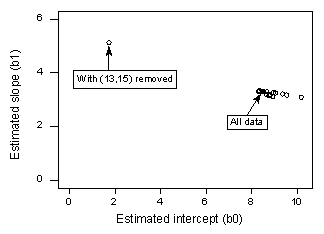
この場合も、黒い実線はn=21のデータポイントすべてに基づく推定係数を表します。 開いている円は、各データポイントを1つずつ削除したときに得られた各推定係数を表しています。 このように、赤いデータポイント（x = 13, y = 15）を除いて、どのデータポイントを削除しても、推定係数はすべて束になっていることがわかります。 これは、赤いデータ点だけが、推定された回帰関数、ひいてはフィット値に不当に影響を及ぼしていることを示唆しています。 この場合、赤いデータ点に対するクックの距離尺度Diは大きく、残りのデータ点に対するクックの距離尺度Diは小さいと予想されます。

クックの距離尺度を使う。 上記の例の良さは、単純なプロットで何が起こっているのかが分かることです。 残念ながら、重回帰の場合は単純なプロットには頼れないのです。 その代わりに、クックの距離尺度がデータ点を影響力のあるものとして扱うことを正当化するのに十分大きいとき、それを決定するガイドラインに頼らなければなりません。

以下、よく使われるガイドラインです：

• Diが0.5より大きい場合、i番目のデータ点は影響力があるかもしれないのでさらに調査する価値があると言える。
• Diが1より大きい場合、i番目のデータポイントは影響力がある可能性が非常に高い。
• あるいは、Diが他のDi値から突出している場合、それはほぼ間違いなく影響力がある。

例2（再び）。 このデータセットのクックの距離尺度を調べてみよう（influence2.txt):

xにyを回帰し、Cookの距離測定を要求すると、次のソフトウェア出力を得ます：

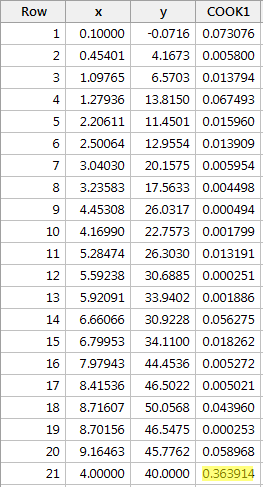
赤いデータポイントのCookの距離測定 (0.363914) は他のCookの距離測定と比較して少し際立っています。 それでも、赤いデータポイントのクックの距離測定は0.5より小さいです。 したがって、クックの距離尺度に基づくと、赤いデータポイントは影響力があるとは分類されません。

例題3（再び）。 このデータセット（influence3.）のCookの距離尺度を確認してみましょう。txt):

x に y を回帰し、Cook の距離測定を要求すると、次のソフトウェア出力が得られます:

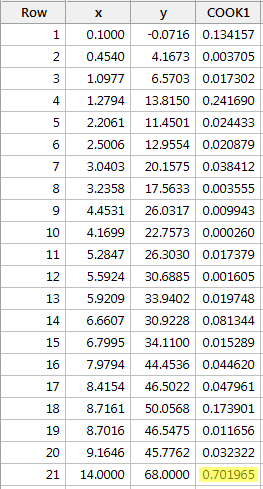
赤いデータ点 (0.701965) に対する Cook の距離測定が他の Cook の距離測定と比べて少し際立っていることがわかりました。 したがって、クックの距離測定に基づいて、さらに調査することはあっても、必ずしも赤のデータポイントが影響力があるとは分類されないでしょう。 このデータセット (influence4.txt) の Cook の距離測定をチェックしてみましょう。

x に y を回帰して Cook の距離測定を要求すると、次のソフトウェア出力を得られます。

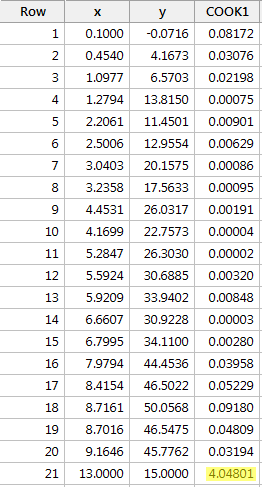
この場合、赤いデータ点 (4.) に対する Cook の距離測定があります。04801)のクック距離測定は、他のクック距離測定と比較して大きく際立っている。 さらに、赤いデータポイントのクックの距離測定は1より大きい。したがって、クックの距離測定に基づいて、驚くことではないが、我々は赤いデータポイントを影響力があると分類する。

時々使われるクックの距離を解釈する別の方法は、F（k+1、n-k-1）分布に測定値を関連付け、対応するパーセント値を見つけることです。 このパーセンタイルが約10％や20％より小さければ、そのケースは適合値にほとんど影響を与えないということになります。 一方、50％近く、あるいはそれ以上であれば、そのケースは大きな影響を与える。 (「その中間」はより曖昧です。)

上