解析幾何学とは?
解析幾何学とは?
解析幾何学は代数学の一分野で、点、(直線)、円といった幾何学的な対象をモデル化するために使用されるものです。 平面解析幾何学では、点は順序付けられた数の組、たとえば (x, y) として定義され、一方、直線は線形方程式を満たす点の集合として定義される(D. Pedoe または D. Brannan 他による優れた解説を参照)。 例えば、任意の2点(x1, y1)と(x2, y2)に対して、これらの点を通る1本の直線ax + by + c = 0が存在する。 その係数a、b、cは、2つの方程式の連立方程式
| ax1 + by1 + c = 0 ax2 + by2 + c = 0から(一定の係数まで)求めることができる。 |
あるいは直接、行列式
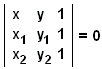 |
しかし、どんな公理主義も未定義の要素を使って逃れることはできません。 数学の多くを支える集合論、特に解析幾何学では、集合の最も基本的な概念は未定義のままである。
3次元空間の幾何学は、3つの数(x、y、z)でモデル化され、3次元線形方程式 ax + by + cz + d = 0 が平面を定義する。 一般に、解析幾何学はより高い次元で作業するための便利なツールを提供する。
解析幾何学の枠組みの中で、非ユークリッド幾何学もモデル化できる(そして実際にモデル化している)。 例えば、平面射影幾何学では、点とは、
| (tx, ty.) のような、すべてが0ではない同次座標 (x, y, z) の三つである。 tz) = (x, y, z), |
for all t ≠ 0, 一方、直線は同次方程式
| ax + bx + cz = 0によって記述される。 |
解析幾何学では、円錐曲線は2次方程式で定義される:
| ax² + bxy + cy² + dx + ey + f = 0. |
解析幾何学の大部分で、線形方程式を扱うものを線形代数と呼ぶ。
Cartesian analytic geometry は軸 x = 0 と y = 0 が垂直である幾何学です。
n タプル x = (x1, …, xn) の成分はその座標として知られています。 4566>
- D. A. Brannan, M. F. Esplen, J. J. Gray, Geometry, Cambridge University Press, 2002
- D. Pedoe, Geometry, 2003
- D. Pedoe, Geometry: A Comprehensive Course, Dover, 1988
|Contact|Front page|Contents|Geometry|Up|
Copyright © 1996-2018 Alexander Bogomolny
Leave a Reply