第14回: ドット積とハダマード積

先に説明した行列の乗算のほかに、ベクトルはもう2つの方法で乗算することができます。 ドット積とハダマード積です。 両者の結果は異なります。

同じ行と列に対応する要素を掛け合わせ、その結果をスカラーになるように足し合わせます。

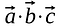
行列の乗算とは異なり、ドットプロダクトの結果は別のベクトルや行列ではなく、スカラーになる。

dot productではベクトルの順序は関係なく、両方のベクトルの要素の数が等しければ良いのだそうです。

ドットプロダクトの幾何学的公式は

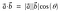
ドットプロダクトは内積またはスカラプロダクトとも呼ばれています。

ベクトルの射影

角度Φ(Ф)を引いた2つのベクトルcとdがあるとします。

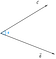
さて、ここで。 ベクトルcのベクトルdへの射影は

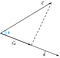
図より射影は角度phi（Ф）に関するベクトルcの水平成分と一致すると考えることができる。

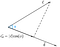
これをスカラー投影と言います。ベクトルcのベクトルdへの投影を求めるには、スカラー投影に単位ベクトルdを掛ける必要がある。

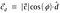
単位ベクトルdを代入した値だ。

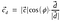
このようになります。 ドットプロダクトは、

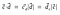
線形代数や機械学習で広く使われています（SVMはデータの分類に用いられる機械学習アルゴリズムです）。

ハダマード積（要素ごとの乗算）

2つのベクトルのハダマード積は、行列の加算に非常に似ており、与えられたベクトル/行列の同じ行と列に対応する要素が一緒に乗算されて新しいベクトル/行列を形成する。

これはフランスの数学者ジャック・ハダマールにちなんで名づけられました。

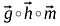
掛ける行列/ベクトルは同じ順番で、結果の行列も同じ順番で乗らなければなりません。

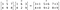
Hadamard productはJPEGなどの画像圧縮技術で使用されています。 ドイツの数学者イッサイ・シュールにちなんでシュール積とも呼ばれています。

ハダマード積は、再帰型ニューラルネットワーク（RNN）のLSTM（Long Short-Term Memory）セルで使用されています。