差分プライバシー入門

Aaruran Elamurugaiyan

プライバシーは数値化することができる。 さらに良いことに、プライバシーを維持する戦略をランク付けし、どれがより効果的であるかを言うことができます。 さらに良いことに、補助的な情報を持つハッカーに対しても堅牢な戦略を設計することができるのです。 さらに、これらのことを同時に行うことも可能です。 これらのソリューションは、差分プライバシーと呼ばれる確率論的理論に存在するものです。 私たちは機密性の高いデータベースをキュレーション (管理) しており、このデータからいくつかの統計を一般に公開したいと考えています。 しかし、私たちが公開したものから敵対者が機密データをリバース エンジニアリングすることが不可能であることを確認する必要があります。 この場合の敵とは、私たちの機密データの少なくとも一部を公開する、あるいは知ろうとする意図を持つ当事者のことです。 差分プライバシーは、機密データ、統計を公開する必要のあるキュレーター、機密データを復元しようとする敵対者、この3つの要素が揃ったときに発生する問題を解決できる（図1参照）。 このリバースエンジニアリングはプライバシー侵害の一種です。

But how hard is it to breach privacy? データを匿名化すれば十分ではないでしょうか？ 他のデータソースからの補助的な情報がある場合、匿名化だけでは十分ではありません。 例えば、2007年、Netflixは、協調フィルタリングアルゴリズムを誰でも上回れるかどうかという競争の一環として、彼らのユーザー評価のデータセットを公開しました。 このデータセットには個人を特定する情報は含まれていませんでしたが、研究者はプライバシーを侵害することができ、データセットから削除されたすべての個人情報の99%を復元しました。 この場合、研究者はIMDBからの補助的な情報を使用してプライバシーを侵害した。

未知の、そしておそらく無制限の、外部からの助けを持つ敵から、誰もがどのように防御できるだろうか？ 差分プライバシーが解決策を提供する。 微分プライバシーアルゴリズムは、補助的な情報を利用する適応的な攻撃に対して回復力がある。 これらのアルゴリズムは、敵が受け取るすべてがノイズとなり、不正確で、プライバシーを侵害することがはるかに難しくなるように、ランダムなノイズを組み込むことに依存しています (実現可能であればの話ですが)。 信用格付けのデータベース（表1でまとめたもの）を管理しているとしよう。

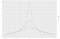
この例では、敵対者が悪い信用格付けを持っている人の数（これは3）を知りたがっていると仮定しましょう。 データは機密なので、グランドトゥルースを明らかにすることはできません。 その代わり、我々はグランドトゥルースであるN = 3にランダムなノイズを加えたものを返すアルゴリズムを使用することにします。 この基本的な考え方（基底真理にランダムなノイズを加える）が、差分プライバシーの鍵となる。 例えば、ゼロ中心のラプラス分布から標準偏差2の乱数Lを選び、N+Lを返すとする。 標準偏差の選択については、数段落で説明する。 (ラプラス分布を知らない人は、図2を参照してください）。 このアルゴリズムを「ノイジー・カウンティング」と呼ぶことにする。

もし無意味でノイズの多い答えを報告するのであれば、このアルゴリズムのポイントは何なのでしょうか。 その答えは、実用性とプライバシーのバランスを取ることができるからです。 私たちは、可能性のある敵対者に機密データを公開することなく、一般大衆が私たちのデータベースから何らかの効用を得ることを望んでいます。

敵対者が実際に受け取るものは何でしょうか。

The first answer the adversary receives is close to, but not equal to the ground truth.表2において応答は報告されています。 その意味で、敵対者は騙され、効用は提供され、プライバシーは保護される。 しかし、複数回試行すると、グランドトゥルースを推定することができるようになる。 この「問い合わせの繰り返しによる推定」は、差分プライバシーの基本的な限界の一つである 。 もし敵が差分プライバシーのデータベースに十分なクエリーを行うことができれば、それでも機密データを推定することができる。 つまり、クエリの回数が増えれば増えるほど、プライバシーが破られることになる。 表2はこのプライバシーの侵害を経験的に示している。 しかし、ご覧のように、これらの 5 つのクエリからの 90% 信頼区間はかなり広く、推定はまだあまり正確ではありません。

その推定はどの程度正確にできるのでしょうか。 図 3 を見てください。ここでは、シミュレーションを数回実行し、結果をプロットしています。

各縦線は95%信頼区間の幅を示し、ポイントは敵のサンプルデータの平均を表します。 これらのプロットの横軸は対数であり、ノイズは独立で同一分布のラプラス確率変数から引かれていることに注意してください。 全体として、平均はより少ないクエリーでよりノイズが多くなります（サンプルサイズが小さいため）。 予想通り、信頼区間は敵がより多くのクエリーを行うにつれて狭くなります（サンプルサイズが増加し、ノイズがゼロに平均化されるため）。 グラフを検査するだけで、まともな推定を行うには約 50 回のクエリが必要なことがわかります。

この例について考えてみましょう。 何よりもまず、ランダムなノイズを追加することで、敵がプライバシーを侵害することを難しくしています。 第二に、私たちが採用した隠蔽戦略は、実装も理解も簡単でした。 残念ながら、より多くのクエリを実行すると、敵対者は真のカウントを近似することができました。

追加するノイズの分散を大きくすれば、データをよりよく防御できますが、隠したい関数に任意のラプラス ノイズを単純に追加することはできません。 なぜなら、加えるべきノイズの量は関数の感度に依存し、関数ごとに感度が異なるからです。 特に、計数関数の感度は1である。ここで、感度が何を意味するのかを見てみよう。

感度とラプラスメカニズム

ある関数について：

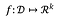
fの感度は次の通りです。

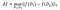
on datasets D₁, D₂ differing at most one element .

上の定義はかなり数学的ですが、見た目ほど悪いものではありません。 大雑把に言うと、関数の感度とは、任意のデータセットについて、1 つの行がその関数の結果に対して持ちうる最大の差のことです。 たとえば、私たちのおもちゃのデータセットでは、行の数を数えることは 1 の感度を持っています。なぜなら、どのデータセットからでも 1 行を追加または削除すると、カウントは最大で 1 だけ変化するからです。

別の例として、「カウントを5の倍数に切り上げる」について考えてみましょう。 この関数の感度は5であり、これを非常に簡単に示すことができる。 サイズ10と11の2つのデータセットがあったとして、それらは1行で異なっていますが、「5の倍数に切り上げられたカウント」はそれぞれ10と15です。 実際、5がこの例の関数が出しうる最大の差である。 したがって、その感度は5である。

任意の関数の感度を計算することは難しい。 感度の推定、感度の推定値の改善、感度の計算の回避にかなりの研究努力が費やされている。

感度とノイジー・カウンティングとの関係は？ 我々のノイジー・カウンティング戦略はラプラス機構と呼ばれるアルゴリズムを使用したが、これは逆にそれが隠蔽する関数の感度に依存している 。 アルゴリズム 1 では、ラプラス機構のナイーブな擬似コード実装があります。 関数F、入力X、プライバシーレベルϵ
Output: A Noisy Answer
Compute F (X)
Compute sensitivity of of F : S
Draw noise L from a Laplace distribution with variance.F (X)を計算する。

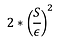
Return F(X) + L

S が大きいと答えはよりやかましくなります。 カウントは1の感度しかないので、プライバシーを守るために多くのノイズを加える必要はない。

アルゴリズム1のラプラス機構がパラメータεを消費することに注目すること。 この量を機構のプライバシー損失と呼び、差分プライバシーの分野で最も中心的な定義である「ε-差分プライバシー」の一部とすることにする。 例として、先ほどの例を思い出し、いくつかの代数を使って説明すると、ノイズの多い計数機構はε0.707のε微分プライバシーを持っていることがわかる。 イプシロンを調整することで、ノイズの多いカウントのノイズを制御することができる。 より小さなεを選択することで、よりノイズの多い結果とより良いプライバシー保証が得られる。 参考までに、Appleはキーボードの差分プライバシーのオートコレクトに2のεを使用している。

εの量は、差分プライバシーが異なる戦略間の厳密な比較を提供することができる方法である。 イプシロン微分プライバシーの正式な定義は、もう少し数学的に複雑なので、このブログ記事では意図的に省略しています。 これについては、Dwork の差分プライバシーのサーベイで読むことができます。

思い出してほしいのですが、ノイズの多いカウントの例のイプシロンは 0.707 で、これは非常に小さいものでした。 しかし、50 回のクエリの後、まだプライバシーが破られました。 なぜでしょうか。 クエリーが増えると、プライバシー予算が大きくなり、したがってプライバシー保証が悪くなるからです。

プライバシー予算

一般に、プライバシー損失は蓄積されます。 二つの回答が敵に返された場合、合計のプライバシー損失は2倍となり、プライバシー保証は半分の強さになる。 この累積的な性質は、構成定理の帰結である。 要するに、新しいクエリーが出るたびに、機密データに関する追加の情報が公開されるのである。 したがって、構成定理は悲観的な見方をしており、新しい応答があるたびに同じ量の漏洩が起こるという最悪のケースを想定している。 強力なプライバシー保証のためには、プライバシーの損失が小さいことが望まれる。 したがって、35 のプライバシー損失（ラプラス ノイズ カウント機構への 50 回のクエリの後）がある私たちの例では、対応するプライバシー保証は壊れやすい。 意味のあるプライバシー保証を確保するために、データキュレーターは最大プライバシー損失を強制することができる。 クエリーの数が閾値を超えると、プライバシー保証が弱くなりすぎて、キュレーターはクエリーの回答を停止する。 最大プライバシー損失はプライバシーバジェット（privacy budget）と呼ばれます。 各クエリーはプライバシーの損失が増加する「支出」であると考えることができる。 予算、経費、損失を使用する戦略はプライバシーアカウンティングと呼ばれるにふさわしい。

プライバシーアカウンティングは複数のクエリ後のプライバシー損失を計算するのに有効な戦略だが、まだ構成定理を取り入れることができる。 先に述べたように、構成定理は最悪のケースを想定している。 言い換えれば、より良い選択肢が存在するということです。

Deep Learning

Deep Learning は機械学習のサブフィールドで、未知の機能を推定するための深いニューラルネットワーク (DNN) のトレーニングに関連する分野です。 (DNNとは、あるn次元空間をm次元空間に写像するアフィン変換と非線形変換の列のことである。） その応用は広く、ここで繰り返し説明する必要はないだろう。 1594>

ディープニューラルネットワークは通常、確率的勾配降下法（SGD）の一種を用いて訓練される。 Abadiらは、一般的に「プライベートSGD」（またはPSGD）と呼ばれる、この一般的なアルゴリズムのプライバシー保護バージョンを発明しました。 図4は、彼らの新しい手法の威力を示しています。 Abadiらは、新しいアプローチとして、モーメント会計を考案しました。 モーメント・アカウンタントの基本的な考え方は、プライバシー損失を確率変数に見立て、その分布の理解を深めるためにモーメント生成関数を用いて、プライバシー損失を蓄積することです（これが名前の由来です）。

Final Thoughts

ここまで、差分プライバシー理論をレビューし、それがどのようにプライバシーの定量化に使用できるかを見てきました。 この投稿の例では、基本的な考え方がどのように適用できるのか、また、適用と理論の間の接続を示しました。 プライバシー保証は繰り返しの使用によって劣化することを覚えておくことが重要です。したがって、プライバシーバジェットや他の戦略であれ、これを軽減する方法を考える価値があります。 この文章をクリックし、実験を繰り返すことで、劣化を調べることができます。 ここではまだ多くの疑問があり、多くの文献を調べる必要があります。 さらに読み進めることをお勧めします。

Cynthia Dwork. 差分プライバシー。 結果の調査。 International Conference on Theory and Applications of Models of Computation, 2008.

Wikipedia Contributors. ラプラス分布、2018年7月.

Aaruran Elamurugaiyan. クエリ数に対する差分プライベート応答の標準誤差を示すプロット、2018年8月.

Benjamin I. P. Rubinstein and Francesco Alda. 感度サンプリングによる痛みのないランダムな差分プライバシーの実現。 In 34th International Conference on Machine Learning (ICML’2017) , 2017.

Cynthia Dwork and Aaron Roth. 差分プライバシーのアルゴリズム的基礎. Now Publ., 2014.

Martin Abadi, Andy Chu, Ian Goodfellow, H. Brendan Mcmahan, Ilya Mironov, Kunal Talwar, and Li Zhang. ディファレンシャルプライバシーを用いたディープラーニング。 Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security – CCS16 , 2016.

Frank D. McSherry. プライバシー統合クエリ。 プライバシーを維持したデータ解析のための拡張可能なプラットフォーム。 In Proceedings of the 2009 ACM SIGMOD International Conference on Management of Data , SIGMOD ’09, pages 19-30, New York, NY, USA, 2009. ACM.

Wikipediaのコントリビューター。 ディープラーニング』2018年8月号.

.