凸包問題のやさしい入門書

凸包はさまざまな分野で役に立つ傾向があり、時には意外なほど役に立つことがあります。 今回は、2次元凸包の基本的な考え方と、それを求めるためのグラハムスキャンの使い方を説明します。 もし、あなたがグラハム・スキャンについてすでに知っているなら、この記事はあなた向けではありませんが、そうでないなら、関連する概念のいくつかに慣れることができるはずです。

ある点の集合の凸包は、集合内のすべての点を囲む最小の凸多角形として定義されます。 凸とは、内側に曲がる角がないこと。

右の多角形の赤い辺は、凸の反対である凹の形をした角を囲んでいます。

凸包を考えるのに便利なのが、輪ゴムのアナロジーです。 集合の中の点が平らな面から突き出ている釘であるとします。 ここで、輪ゴムを取って釘の周りに伸ばしたらどうなるか、想像してみてください。 元の長さに縮めようとすると、輪ゴムは釘を囲み、中心から最も突き出ている釘に触れることになります。

結果として得られる凸包をコードで表現するには、通常、この輪ゴムを支える点のリスト、つまり凸包上の点のリストを保存します。

3 つの点が同じ線上にある場合に何が起こるべきかをまだ定義する必要があることに留意してください。 輪ゴムが1本の釘に接触する点があるが、そこでは全く曲がらないことを想像すると、そこの釘は他の2本の釘の間の直線上にあることを意味します。 問題によっては、この直線上の釘は輪ゴムに触れているので、出力の一部と考えるかもしれません。 一方、輪ゴムを取り除いても輪ゴムの形は変わらないので、この釘は出力の一部であってはならないと言うかもしれません。 この判断は現在取り組んでいる問題に依存しますし、何より、3 つの点が平行でない入力がある場合（プログラミング競技の簡単な課題ではよくあります）、この問題を完全に無視することもできます。

凸包を求める

点の集合を見て、人間の直観はどの点が凸包に触れそうか、どの点が中心に近く、したがって凸包から離れそうかをすぐに把握できます。

点の集合の凸包を求めるには、計算幾何学の最初のアルゴリズムの 1 つと考えられているグラハム スキャンと呼ばれるアルゴリズムを使用することができます。 このアルゴリズムを用いて、凸包上にある点の部分集合と、これらの点が凸包の周りを回るときに遭遇する順序を求めることができる。

このアルゴリズムは、まず確実に凸包上にあることが分かっている点を見つけることから始まる。 例えば、y座標が最も小さい点は安全な選択であると考えられる。 同じy座標に複数の点が存在する場合、x座標が最も大きい点を選択します（これは他のコーナー点でも同様に機能し、例えば最初にxが最も小さく、次にyが最も小さくなります）。

次に、始点から見た他の点の角度で並び替えを行います。

さて、このアルゴリズムのアイデアは、すべての点に対して、それが凸包上にあるかどうか決定しながらこの並び替えられた配列上を歩くことである。 つまり、3つの点が重なるごとに、それらが凸コーナーか凹コーナーかを判断するのです。

（凹角、凸角という言葉は多角形全体に対して使わなければならないことに注意してください。)

凸包上にある点をスタックに格納します。そうすれば、ソートされた点を回っている途中で到達したら点を追加し、凹角を形成することがわかったら削除することができます。

(厳密には、スタックの上位 2 点にアクセスする必要があるので、代わりに std::vector を使用しますが、常に上位 2 要素にしか関心がないので、スタックの一種として考えます。)

点のソートされた配列を回って、点をスタックに追加し、後で点が凸包に属さないことがわかったら、それを除去します。

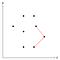
クロスプロダクトを計算してそれが正か負かを調べることにより、現在のコーナーが内側に曲がっているか外側に向かっているか測定することが可能です。 上の図は、3つの点が凸になっているので、3つの点のうち真ん中の点をスタックに残します。

次の点に行っても、同じことを繰り返します。角が凸かどうかを調べ、そうでなければ、点を削除します。

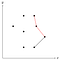
この赤で示した角は凹なので、凸包に含まれないとしてスタックから中点を削除します。

これで正しい答えが得られるとどうしてわかるのでしょうか。

厳密な証明を書くことはこの記事の範囲外ですが、基本的な考え方は書けます。 しかし、その隙間を埋めていくことをお勧めします！

すべての角でcross productを計算したので、凸多角形になっていることは確かなことです。 あとは、この凸多角形が本当にすべての点を囲んでいることを証明するだけです。

（実際には、この条件を満たす最小の凸多角形であることも示す必要がありますが、それは凸多角形の角点が元の点集合の部分集合であることから非常に簡単に導かれます。)

今見つけた多角形の外側に点Pがあるとします。

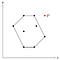
すべての点は一度スタックの上に追加されていますので、ある点でPがスタックから外されたことが分かっています。

OとQは多角形の内側（または境界）にあるので、Pも境界の内側になければならない。多角形は凸であり、OとQがPと作る角は多角形に対して凹である。

実装

ここで提供する実装は、点を含むstd::vectorをstd::pair個のintとして受け取り、凸包上にある点を含む別のstd::vectorを返す関数convex_hullを持っています。

Runtime and memory analysis

複雑なアルゴリズムについて Big-O notation の観点から考えることは常に有用ですが、ここでの説明はしません。 すべてのポイントは最大 1 回だけスタックに追加およびスタックから削除されるため、最悪の場合の実行時間は O(n log n) になります。

現時点で O(n) になるメモリ使用量は、スタックの必要性を排除し、入力配列で直接操作を実行することで最適化できます。 凸包上にある点を入力配列の先頭に移動して正しい順序で並べ、他の点は配列の残りに移動させればよいのです。 この関数は，配列中のどの程度の点が凸包上にあるかを表す1つの整数型変数を返すだけです． もちろん、この方法には、関数がより複雑になるという欠点があります。したがって、組み込みシステム用にコーディングしている場合や、同様にメモリに制約がある場合を除き、この方法はお勧めできません。 ほとんどの場合、バグの確率とメモリ節約のトレードオフは、それに見合うものではありません。 しかし、グラハム・スキャンがどのように機能するかを最初に理解することは意味がある。

もし本当に空想的で3次元の問題に取り組みたいなら、1977年の論文「2次元と3次元における有限の点集合の凸包」で紹介したプレパラータとホンのアルゴリズムを見てみるとよい。