ヘルムホルツ共鳴
- ヘルムホルツ共鳴の解析
- 共振、インピーダンス、位相、周波数依存性
- 長さに関わる複雑さ
ヘルムホルツ共鳴とギター
Helmholtz resonance
それでは定量的に見ていこうと思います。 まず、発生する音の波長が共鳴器の寸法よりずっと長いと仮定します。 このページの一番上にあるアニメーションの瓶の場合、波長はそれぞれ180cmと74cmなので、この近似はかなり良いのですが、何かをヘルムホルツ振動子として記述し始める時には、必ず確認する価値があります。 この近似の結果、容器の体積内の圧力の変化を無視することができます。
首の中の空気の有効長をL、断面積をSとすると、その質量は空気の密度ρのSL倍です(有効長についてはこのページの最後でややこしいことを述べています)。 この空気の「栓」が瓶の中を少しxだけ下降すると、容器内の空気を圧縮して、それまで体積Vを占めていた空気が、V-Sxの体積を持つようになります。 その結果、その空気の圧力は大気圧PAからPA+pという高い値まで上昇します。 圧縮が非常にゆっくり行われ、温度が変化しない場合はそうなります。 しかし、音を出す振動では、変化が速いので、圧縮時に温度が上昇し、圧力の変化が大きくなります。 技術的には断熱的であり、熱が移動する時間はなく、結果として式には比熱の比である定数γが含まれ、空気では約1.4となる。 (これは付録で説明します。) その結果、小さな体積変化ΔVによって生じる圧力変化pはちょうど
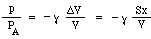
ここで質量mは首の上と下の圧力差、すなわち正味の力pSによって移動するので、加速度aについてニュートンの法則を書いてみましょう。
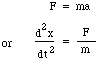
Fとmを代入して次のようになる。 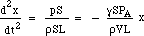
つまり復元力は変位に比例する。 これが単純調和運動の条件であり、比例定数の平方根の1/2π倍の周波数を持つので、
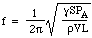
さて、空気中の音速cは密度と圧力と比熱の比で決まるので、こう書けます。
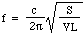
数字を入れてみましょう。S=3平方センチメートル、L=5センチメートルの1リットル瓶の場合、周波数は130Hzで、中音の下のCくらいです(注参照)だから波長は2.6メートルで、瓶よりずっと大きいですね。 これで、導出の最初に立てた仮定が、事後的に正当化される。
共振、インピーダンス、位相、周波数依存性
この節だけでも読めますが、より詳しい背景が知りたい場合は、発振、強制発振、音響コンプライアンス、イナーダンス、インピーダンスを参照してください。
機械的な表現に戻り、最初の模式図のようにヘルムホルツ共鳴器を外側から見てみましょう:私たちは振動力Fで、周波数fで、質量m(共鳴器の首の部分の空気)を押しており、それはバネ定数kで、反対側が固定(共鳴器の中の空気は逃げられない)されたバネ(封じられた空気)で支えられています。 非現実的だが、重力と摩擦は(今のところ)無視することにする。
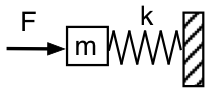
質量を加速するのに必要な力は加速度に比例するのでf2に比例します。 十分低い周波数では質量を加速するのに必要な力は無視できるのでFはばねを圧縮し伸ばせばいいだけです。 ですから、その極限では、加わる力F=+kxとなります。 (バネの力は-kxです。) この低周波数での系の機械的インピーダンスは、コンプライアント、つまりバネ的です。 音響的には、ネックの空気の固まりを押して、レゾネータの空気を圧縮する、アコースティックコンプライアンスに見えます。 右側にかかる力Fは、右側に測ったxと同位相なので、速度の90°後ろ、かかる圧力は共鳴器への音響的な流れの90°後ろとなります。
加速度のf2依存性を覚えておいてください。 つまり、十分に高い周波数では、バネの力は質量を加速する力に比べて無視できるほど小さくなる。 つまり、Fは加速度と同位相で、速度の90°前にあることになります。 音響的には、加圧された圧力は、共振器内に流入する音響流の90°前にあることになります。 機械的、音響的に不活性なのです。
共振周波数(やはり上のスケッチの話)においては、非常に小さな力でも振幅が大きくなることがあります。 ですから、共振時には、外部から質量に加えられる力から見ると、インピーダンスは非常に低くなります(上の図)。 共振時には、共振器への流入と流出が最大となる。
ここで、共振器内部(ネックから離れたところ)の圧力に注目するとどうなるか考えてみましょう。 ここではバネにかかる力を見ているので、機械的なアナログは次のような回路図になります。
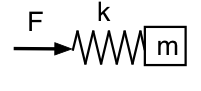
今回の低周波は、与えられた振幅に対して力を小さくできることです。バネと質量は質量として一緒に動き、今回のシステムは低周波では慣性に見えます。 高周波では質量はほとんど動かず、バネ的な、あるいはコンプライアンス的な系になります。 つまり、位相関係は以前とは逆で、低周波ではpがUを90°リードし、高周波ではpがUを90°遅らせることになる。
有効長に関する問題
このページの最初の図では、空気の「栓」があたかも円筒で、ボトルの首の両端できれいに終わるかのように描かれています。 これは単純化しすぎである。 実際には、上のアニメーションが示唆するように、首の中の空気とともに、内側と外側の余分な体積が移動します。 首の幾何学的長さに加えられるべき余分な長さは、通常(そして非常におおよそ)、外側端の半径の0.6倍、内側端の半径の1倍となります)。
|
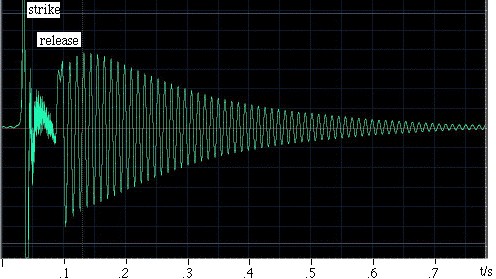
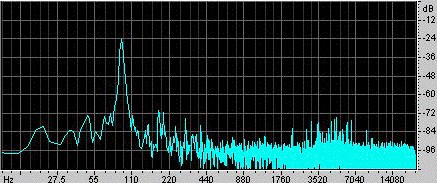
一例を挙げます。 ラ・インタはこの例を作った。 彼は体積0.00292m3の球形のヘルムホルツ共鳴器と長さ0.080m、断面積0.00083m2の円筒形のネックを取り出した。 これを励起するために、手のひらで叩いてから離した。 共振器の中にあるマイクロホンで音を記録すると、左のオシログラムのようになる。 手が振動子を押さえる時間は0.1秒未満で、この間は振動が弱く、周波数も比較的高いことがわかります。 手を離すと振動が発生し、粘性と乱流抵抗、そして音の放射によってエネルギーを失い、徐々に消えていきます。 よく観察すると、手が開放端から離れるにつれて周波数がわずかに上昇しています。これは、手が放射に利用できる立体角を制限し、端部効果(または端部補正)を増大させるからです。 ネックの長さはバッフル付きとバッフル無しのエンドエフェクトで1つずつ増え、有効長は0.105mとなります。音速を343m/sとすると、上の式から共振周波数は90Hzとなります。 |
|
Helmholtz resonances and guitars
* ギターのボディ内の空気はほとんどヘルムホルツ振動子のように作用すると上に述べました。 このケースは、ボディ内の気圧が上昇するとボディが少し膨らむので複雑です。また、ギターのサウンドホールの「中」の空気は、瓶のネックの中の空気よりも簡単に可視化できない形状をしています。 実際、ギターのボディの場合、空気のプラグの長さは、わずか数mmの太さの「パイプ」の先端にある2つの「エンドエフェクト」とほぼ等しいのです。 しかし、エンドエフェクトは穴の半径に関係し、同じような大きさなので、空気の質量は相当なものになります。 無限大の平面バッフルに開口する円筒形パイプのエンドエフェクトの長さは、パイプの半径の0.85倍です。 ギターのサウンドボードは無限ではありませんが、同様の効果が期待できますので、空気の「栓」の有効長さは穴の半径の約1.7倍となります。 (メーカーによっては、サウンドホールの下に同じ半径の短いチューブを固定することで、これを大きくしています)。
何人かの方から、ある楽器のサウンドホールの大きさはどのくらいがいいのか、というご質問をいただきました。 この質問には、上の式で答えることができます。 しかし、ボディの膨らみが重要です。 そうすると、空気の「バネ」がむしろ柔らかくなり、周波数が低くなるのです。 純粋なヘルムホルツ共鳴は、体の体積を一定に保つことで調べることができます。 これを測定する場合、ボディーの膨張や「呼吸」を妨げるためにギターを砂に埋めるのが一般的な方法です。 しかし、ギターは通常このような状況で演奏されることはありません。 そのため、ヘルムホルツの計算では、実際の柔軟なボディの共振周波数は過大評価されてしまうのです。
ここで、半径rの円形のサウンドホールを想定して、S=πr2、L=1.7rと説明しました。 c=340m/sとしてヘルムホルツ振動数の式に代入すると、次のようになります。
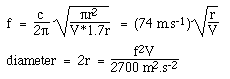
SI標準単位を使用していることに注意してください。音速をメートルと秒単位で使用したので、メートル単位の答えを出すには、体積は立方メートル、周波数はヘルツでなければなりません。
トーンホールが円形でない場合は、同じ面積の円の場合と最終的な効果が等しくならないので、より複雑になります。 博士課程の学生でルシアーのJohn McLennanがこれに関する測定レポートを書いていますので、近日中にここに掲載します。
ギターやバイオリン系の楽器では、ヘルムホルツ(+ボディ)の共振が、バイオリンのD、ギターのG-Aのあたり、2番目に低い弦の周波数の近くか少し下にあることが多いのですが、この共振を利用すると、2番目に低い弦の周波数が低くなります。 穴の全部または一部を適当な形の硬いボール紙で覆うことで、ヘルムホルツの周波数を大幅に下げたりずらしたりすることができます。 そして、共振点付近で音を出してから、厚紙をスライドさせ、穴を交互に覆ったり出したりすると、共振の効果をはっきりと聞き取ることができます。
0.85rの効果は妥当なのか? 私たちの研究室でギター音響の博士号を取得したRa Intaは、興味深いデモを提案しています:
ギターの弦を振動しないように湿らせます(例えば、弦と指板の間にハンカチを挟みます)。 片方の手のひらをサウンドホールの上に持っていき、サウンドホールに近づけます。 もう片方の手の指で、サウンドボードのサウンドホール付近と1弦付近を鋭く叩きます。 手のひらに空気の鼓動を感じるはずです。 このとき、指がサウンドボードを押し込むことで、ボディから空気が押し出されます。 次に手を徐々に穴から離し、指で叩き続けます。 空気の動きを感じなくなるのはいつ頃でしょうか? これで、サウンドホールの場合、「エンドエフェクト」の長さの目安がわかります。
Tuning the Helmholtz resonance
この研究室の博士課程学生John McLennanの論文に、音速を変化させてHelmholtz共鳴を変化させるというものがあります。
- McLennan, J.E. (2003) “A0 and A1 studies on the violin using CO2, He, and air/helium mixtures.”. Acustica, 89, 176-180.
Thomas B. Greenslade (Kenyon College, Ohio) より提供された歴史的なヘルムホルツ共鳴器の写真をいくつか掲載します。
Leave a Reply