フィボナッチ級数のアルゴリズムとフローチャート

フィボナッチ級数は、最初の2つの数字が1と1、または0と1で、選択した開始点に応じて、続く各数字が前の2つの数字の合計になる数列と定義されます。 つまり、この系列では、第n項は（n-1）項と（n-2）項の和となる。 このチュートリアルでは、フィボナッチ級数の簡単なアルゴリズムとフローチャート、およびフィボナッチ級数とその重要な特性のいくつかを説明します。

Fibonacci Series Algorithm and Flowchart のソースコードを見てもらう前に、まずこの素晴らしい級数、その数学的派生と特性についていくつかのことを説明させていただきます。 フィボナッチ級数については、以前の記事 – C Program for Fibonacci Series で詳しく説明しています。 リンク 2.

フィボナッチ級数の生成方法

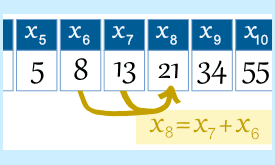
Mathematically, the nth term of the Fibonacci series can be represented as:

tn = tn-1 + tn-2

the Fibonacci numbers up to certain term can be represented as.数学的手法ではフィボナッチ級の第n項は次のように表されます。 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144….あるいは 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…

これはフィボナッチ級数のアルゴリズムとフローチャートに使われる主要特性である。 0か1のどちらかで始まり、その次の項の和は、次のように前の2項の和となる。

First Term = 0
Second term = 1
Third Term = First + Second = 0+1 =1
Fourth term = Second + Third =1+1 = 2
第5項 = 第3+第4 = 2+1 = 3
第6項 = 第4+第5 = 3+2 = 5
第7項 = 第5+第6 = 3+5 = 8
第8項 = 第6+第7 = 5+8 = 13 …となります。 というように、無限に続くのです

フィボナッチ数列のアルゴリズム。

• Start

変数 i, a,b , show

• 初期化 a=0, b=1, およびshow =0
• 表示するフィボナッチ級数の項数を入力
• 級数の最初の2項を表示
• 次のステップでループを使用
  -…する。> show=a+b
  -> a=b
  -> b=show
  -> iの値を1ずつ増やす
• End

フィボナッチ系列のフローチャートを掲載します。

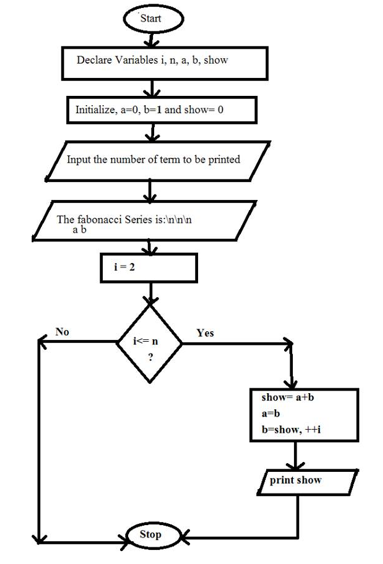
Fibonacci Series C Program
Pascal’s Triangle Algorithm/Flowchart
Tower of Hanoi Algorithm/Flowchart

も参照して下さい。