バイリニアフィルタリングとバイリニア補間

下の絵を見てください。 点A、B、Cの値を計算できますか？

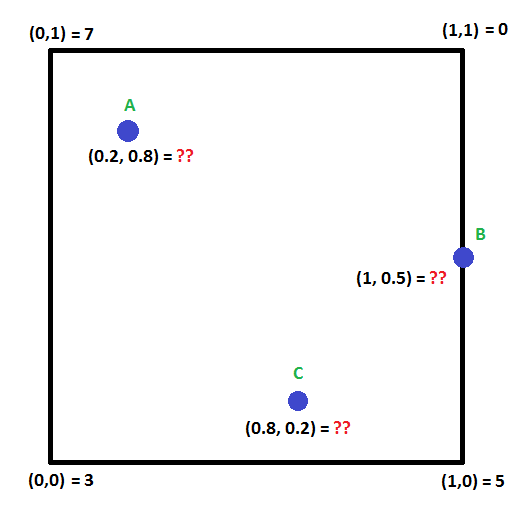
これを行う手法として、線形補間の考え方を2次元に拡張したバイリニア補間というものがあります。

バイリニア補間を計算するには、片方の軸で線形補間を行い、もう片方で行うだけです。

以下の例を見てみましょう。 まずはX軸からです。

まず、X軸の正方形の上部を横切るように補間を行います。 つまり、7から0まで0.2（20％）進む必要がある。この0.2がX軸の座標となる。
7 + (0-7) * 0.2 = 5.6

次に、X軸の正方形の底を横切る補間を行います。 つまり、上と同じように、3から5まで0.2（20％）ずつ進むことになります。
3 + (5-3) * 0.2 = 3.4

X 軸の補間が終わったので、Y 軸を補間する必要があります。 下の値(Y=0の値)から上の値(Y=1の値)まで、0.8(80%)の距離を移動することになります。

ですから、3.4から5.6まで0.8(80%)進む必要があるのです。
3.4 + (5.6 – 3.4) * 0.8 = 5.16

つまり、点Aでの値は5.16となるわけだ。

点 B

点 B の座標は (1.0,0.5) です。

再び X 軸補間から始めてみましょう (もしそうなら、Y から始めても簡単です)。 答えはおわかりかと思いますが、ここで計算します。
7 + (0-7) * 1.0 = 0

同様に、下を横切る X 軸補間を行いましょう。
3 + (5-3) * 1.0 = 5

次はY軸の補間になります。
5 + (0-5) * 0.5 = 2.5

そこで、点Bの値は2.5となります。 これも図を見ればわかるはずです。

点 C

点 C の座標は (0.8,0.2) です。

もう一度、ボックスの上部を横切る X 軸補間を行いましょう。 7 から 0.8 (80%) 進む必要があります。
7 + (0-7) * 0.8 = 1.4

次に、ボックスの下部を横切る X 軸補間を行う必要があります。
3 + (5-3) * 0.8 = 4.6

最後に、Y軸の補間です。 4.6から1.4まで0.2（20%）進む必要があります。
4.6 + (1.4-4.6) * 0.2 = 3.96

点Cの値は、3.6です。96

バイリニア フィルタリング

バイリニア補間は、値を補間したいデータのグリッドがある場合に便利ですが (たとえば、地形を表す高さフィールドなど!)、ゲーム開発においてこれが本当に輝くのは、バイリニア テクスチャ フィルタリングです。

基本的に、テクスチャ座標がテクスチャ内のピクセルの中心に完全に一致しない場合 (余りがあるため)、そのピクセル内の座標の小数部分を使用して、関係する 4 ピクセル間でバイリニア補間を行い、最終的にピクセル色を出します。 これは各チャンネルでバイリニア補間を行います。

最終結果はかなり良好です! 下の画像で、拡大しすぎたテクスチャでこの機能が動作していることを確認してください。 左側はバイリニア フィルタリングを使用し、右側は使用せず、単に最も近いピクセルを表示します。

その結果、バイリニア テクスチャ フィルタリングは、最近接ピクセル サンプリングの場合のように 1 ピクセル読み取りではなく、それらの間で補間できるように 4 ピクセル読み取りを行う必要があります。 より多くのピクセル読み取り＝より多くのオーバーヘッド、そして、使用するのにそれほど安くはありません。

リンク

これを読んでいる一部の人々にとって、この情報はかなり基本的で、なぜ私がそれについてわざわざ書くのかと思うかもしれません。 次の投稿ではバイリニアフィルタリングに関する奇妙なことを紹介します。 これは、次にお見せするものへの足がかりとして必要だったのです😛

Wikipedia.pdf 線形補間

Wikipedia: バイリニア補間

Wikipedia: バイリニア フィルタリング

The Dark Side of Bilinear Filtering

ハードウェア ベースのバイリニア サンプリングの欠点（および回避策）についての詳細情報は、以下のリンクをチェックしてみてください。