デコンボリューション入門

デコンボリューションは、計算量の多い画像処理技術で、顕微鏡で撮影したデジタル画像のコントラストと解像度を改善するために利用されることが多くなっています。 その基礎は、対物レンズの限られた開口部によって引き起こされる顕微鏡画像に存在するぼかしを除去または反転するように設計された一連の手法に基づいています。

デジタル蛍光顕微鏡で取得したほぼすべての画像はデコンボリューションできますし、いくつかの新しいアプリケーションも開発されていて、さまざまなコントラスト向上戦略の下で収集した透過光画像にデコンボリューション技術を適用します。 デコンボリューションによる改良の対象として最も適しているのは、一連の光学的断面から構成される3次元モンタージュである

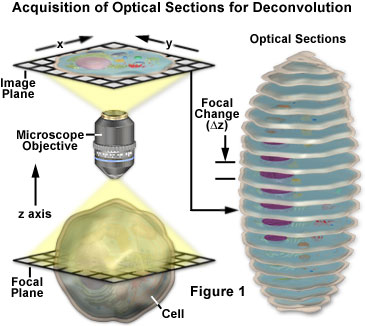
デコンボリューション解析のためのZ系列画像の取得に関する基本概念を、図1に模式図で示した。 一連の画像は、z軸に沿って互いにわずかにずらした状態で記録される。 この焦点面の変更により、現在のz平面の上下から来る焦点外れの光による微妙な変化で、わずかに異なる画像が得られます。 デコンボリューション解析では、z シリーズ全体を解析し、焦点のずれた蛍光によって混乱することのない、より明確で高解像度のデータセットを作成します。

デコンボリューションは、共焦点顕微鏡の良い代替手段としてよく提案されますが、これはどちらの技術も最終画像における焦点のずれた蛍光の影響を最小限にしようとするためです。 共焦点顕微鏡のピンホール開口を用いて得られた画像はデコンボリューション処理の恩恵を受けるので、これは厳密には正しくありません。 共焦点顕微鏡では、対物レンズと検出器の間にピンホール開口を設け、焦点の合った光線のみを通過させることで、焦点の外れた光が検出されるのを防いでいます。 一方、広視野顕微鏡では、焦点の合っていない光を直接検出器まで通過させることができます。 広視野顕微鏡では、焦点の合っていない光を直接検出器に導くことができるため、検出された画像から焦点の合っていない光を除去したり、光源に戻したりするデコンボリューション処理を行います。 共焦点顕微鏡は、胚や臓器などの厚い試料の観察に特に適しており、広視野デコンボリューション処理は、極端に低い光量を必要とする試料のイメージングに強力なツールであることが証明されています。 これらのツールを組み合わせることで、共焦点顕微鏡で取得した画像のノイズを低減させることも可能です。 しかし、文献で報告されているデコンボリューション実験の大部分は、標準的な広視野蛍光顕微鏡で記録された画像に適用されます。

画像劣化の原因

画像の劣化は、ノイズ、散乱、グレア、およびぼかしという 4 つの独立したソースに分けられます。 図 2 は、同じ画像に対するこれらの視覚的影響の例を示しています。

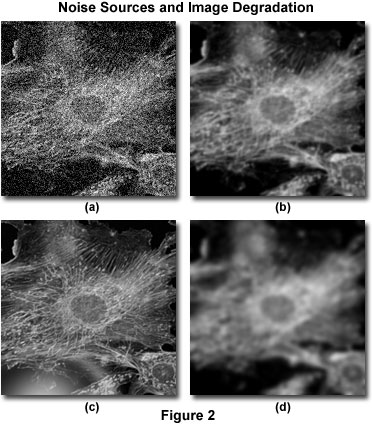
ノイズは、画像内の詳細の準不規則な乱れとして記述でき、（最も厳しい形で）ホワイトノイズまたは塩コショウノイズ、放送テレビの受信不良時に見られるものと同様の外観を持っています（図 2 (a) を参照）。 このようなノイズは、発生源のメカニズムがわかっていれば統計的な分布を予測できるため、「準ランダム」と呼ばれている。 デジタル顕微鏡の場合、主なノイズ源は信号そのもの（フォトンショットノイズと呼ばれることが多い）か、デジタル画像処理システムである。 両ノイズ源のメカニズムは理解されているので、ノイズの統計的分布は既知である。 信号依存のノイズはポアソン分布で特徴付けることができ、一方、イメージングシステムから生じるノイズは多くの場合ガウス分布に従います。 デジタル画像における一般的なノイズの発生源と分布は非常によく理解されているので、適切な画像フィルタを適用することで容易に除去することが可能で、通常、ほとんどのデコンボリューションソフトウェアパッケージにオプションの「プリプロセッシング」ルーチンとして含まれています。 散乱の正味の効果は、図2(b)に示すように、画像の細部が本当にランダムに乱されることです。 ある特定の試料における散乱を予測するための完全に満足できる方法は開発されていませんが、散乱の程度は試料の厚さ、試料と周囲の埋め込み材料の光学的性質に大きく依存することが実証されています。

散乱と同様に、グレアは光のランダムな乱れですが、標本内ではなく、顕微鏡の光学要素（レンズ、フィルター、プリズムなど）で発生します。 現代の顕微鏡では、反射防止コーティングを施したレンズやフィルターの採用、レンズ成形技術、光学セメント、ガラス配合の改良により、グレアは最小限に抑えられています。 図2(c)は、制御されていないグレアの効果を示している。

ブレは、イメージングシステムの光路を通過する際に発生する光の非ランダムな広がりによって説明される（図2(d))。 ボケの最も大きな原因は回折であり、ボケのみで解像度が制限される画像は回折限界であると考えられる。 これは、あらゆる撮像システムの本質的な限界であり、光学システムの解像度限界を評価する際の決め手となる。 幸いなことに、光学顕微鏡のボケの精巧なモデルがあり、これを利用することでピンぼけ光子の発生源を特定することができます。 これがデコンボリューションの基礎となる。 デコンボリューションにおける基本的な重要性から、このセクションの他の部分で、ぼけの理論モデルについてより詳細に説明する。 しかし、すべてのイメージングシステムは、被検体や付属の機器エレクトロニクスによって引き起こされる他の形態の画像劣化とは無関係にぼかしを生成することを強調しておく必要があります。 まさに、光学的なぼかしが他の劣化から独立しているからこそ、デコンボリューション技術によるぼかし除去の可能性があるのです

光と物質の相互作用は、散乱、グレア、ぼかしの主要な物理的原因です。 しかし、ある物質（ガラス、水、タンパク質など）中の分子の組成や配置は、それぞれの物質に固有の光学的特性を与えている。 デコンボリューションでは、散乱、まぶしさ、ぼやけを区別するのは、それらが発生する場所と、これらの現象に対する数学的モデルの生成の可能性である。 散乱は被検体内で局所的かつ不規則に発生する現象であるため、モデル化が困難であった。 一方、ボケは顕微鏡の光学系（主に対物レンズ）の機能であるため、比較的簡単にモデル化することができます。 このようなモデルにより、数学的にぼかしを反転させることが可能となり、デコンボリューションではこのモデルを用いてぼかしを反転させたり除去したりすることができます。 この概念はデコンボリューションにとって基本的に重要であり、イメージングアーチファクトを回避するために明確に理解する必要がある。 点拡がり関数は、標本（物体）空間から発せられる無限に小さい点光源に基づいています。 顕微鏡イメージングシステムは、この点から発せられる光の一部しか集めないため、光を点の完全な3次元画像に集光することができません。 その代わりに、点は3次元の回折パターンに広がって見える。

利用するイメージングモード（広視野、共焦点、透過光）によって、点広がり関数は異なる独自の形状や輪郭を持っている。 広視野蛍光顕微鏡では、点広がり関数の形状は、輪が広がるフレアによって囲まれた長方形の「サッカーボール」のようなものです。 点拡がり関数を3次元で表現するには、x、y、zの3軸の座標系を適用するのが一般的で、xとyは試料の焦点面に平行で、zは顕微鏡の光軸に平行である。 この場合、点広がり関数はx-y平面では同心円の輪の集合として現れ、x-z平面とy-z平面では砂時計のように見える（図3参照）。 広視野の点広がり関数の中心を通るx-yスライスは、同心円の輪の集合を明らかにする。 光軸は画像の縦軸に平行である。 左の点広がり関数は球面収差が小さく、右の点広がり関数は収差が大きいことがわかる。 右の画像では、光軸に沿った中心節が非対称で広がっているため、軸方向の解像度が低下し、信号がぼやけていることに注意。 理論的には、点広がり関数の大きさは無限大で、焦点から遠い面の光の総和強度は、焦点での総和強度と等しくなります。 しかし、光強度はすぐに低下し、やがてノイズと区別がつかなくなる。 高開口数（1.40）の油浸対物レンズで記録した無収差点広がり関数では、焦点面では0.2平方マイクロメートルの光が、焦点の上下1マイクロメートルではその90倍に広がっています。 この点拡がり関数の画像を記録するために使用した試料は、グリセロール（屈折率1.47）にマウントした直径0.1マイクロメートルの蛍光ビーズで、浸漬液は図に示した屈折率であった

重要視すべき点は点拡がり関数が顕微鏡での結像にどのように影響するかである。 結像の理論モデルでは、点拡がり関数を画像の基本単位として扱います。 つまり、家にとってのレンガのように、画像にとっての点拡がり関数なのです。 画像は点拡がり関数の集合体であり、倍率を上げてもこの事実は変わりません。 理論光学の有名な教科書（Born and Wolf: Principles of Optics）によると、「接眼レンズの出力を上げることによって、主画像にない詳細を引き出すことは不可能であり、主画像のそれぞれの要素は小さな回折パターンであり、接眼レンズで見る実際の画像は、これらのパターンの拡大画像の集合にすぎない」

例として、カバースリップと顕微鏡スライド間に挟まれたサブ解像度蛍光ビーズの集団について考えてみましょう。 この標本の焦点の合った画像では、点の雲が見えるが、これは実際には小さな輪のセットに囲まれた円盤である（事実上、エアリーディスクである；図4（a）を参照）。 この標本のピントを少し外すと、ピントが合っていた場所に、より大きな同心円の輪が現れる（図4(b)）。 この試料の三次元画像を収集すると、各ビーズについて完全な点広がり関数が記録される。 点広がり関数は、イメージングシステムを通過した後の各点光源に何が起こるかを記述する。

今述べたぼかし処理は、数学的には畳み込みとしてモデル化される。 コンボリューション操作は、標本内のすべての点への点広がり関数の適用を記述します。標本内の各点から放射された光は、点広がり関数でコンボリューションされて最終的な画像が作成されます。 しかし、この畳み込み演算により、被写体内の点が画像上でぼやけた領域になってしまいます。 画像中の各点の明るさは、畳み込み演算によって、標本中の各点の蛍光に線形に関係する。 点拡がり関数は3次元であるため、点拡がり関数によるボケは本質的に3次元の現象である。 どの焦点面からの画像も、その面に位置する点からのにじんだ光と、他の焦点面に由来する点からのにじんだ光が混在しています

この状況を要約すると、画像は被検体と点広がり関数のコンボリューションによって形成されていると考えることができます。

点拡がり関数の収差

点拡がり関数は、回折の数学的モデルを用いて理論的に定義するか、蛍光ビーズの三次元画像を取得して経験的に定義することができる（図3参照）。 理論的な点広がり関数は、一般に軸方向と半径方向に対称性を持っている。 つまり、点広がり関数はx-y平面の上下に対称（軸対称）であり、z軸を中心とした回転対称（半径対称）である。 経験的な点広がり関数は、完全な対称性から大きく外れることがあります（図3に示すように）。 この偏差は、一般に収差と呼ばれ、イメージングシステムの光学系、特に対物レンズ、ミラー、ビームスプリッター、チューブレンズ、フィルター、ダイヤフラム、アパーチャーなどのコンポーネントの不規則性やミスアライメントによって生じます。 光学部品の品質が高く、顕微鏡のアライメントが良好であればあるほど、経験的点広がり関数は理想的な対称形状に近づきます。 共焦点顕微鏡もデコンボリューション顕微鏡も、点広がり関数ができるだけ理想に近い状態であることが重要なのです。 この収差は、点広がり関数の形状が軸方向に非対称になり、それに伴って特にz軸方向に大きさが増大する(図3)。 その結果、解像度と信号強度が大幅に低下する。 実際には、球面収差の典型的な原因は、対物レンズの浸漬媒体と試料が浸されるマウント媒体の屈折率の不一致である。 この収差を最小限に抑えることが非常に重要である。 デコンボリューションは、失われた解像度を部分的に回復することができるが、いくら画像処理を施しても、失われた信号を回復することはできない。

Lutz H. Schaefer – Advanced Imaging Methodology Consultation, Kitchener, Ontario, Canada.

Jason R. Swedlow – Division of Gene Regulation and Expression, School of Life Sciences Research, University of Dundee, Dundee, DD1 EH5 Scotland.

。