グリーン関数

一般的には、「グリーン関数」と呼ばれます。 グリーン関数は積分カーネルで、初期値や境界値条件のある常微分方程式のような簡単な例から、境界条件のある不均質偏微分方程式（PDE）のような難しい例まで、多くの族の微分方程式を解くために使用することができます。 グリーン関数は、力源や点に集中する電荷に関連する作用を視覚的に解釈することができるため（Qin 2014）、応用数学の分野で特に有用である。 特に、グリーン関数法は、以下のような分野で広く用いられている。 物理学、工学などで広く用いられている。

より正確には、あるユークリッド空間の部分集合上の分布の集合に働く線形微分演算子が与えられると、グリーン関数 、に対応するOmega”>の点

ここではdelta関数である。 このような関数を定義する動機は広く知られているが、上記の恒等式に関数を掛けてに関して積分すると

(2)

右辺はデルタ関数の性質により、単にに還元されるだけ。 であり、はにのみ作用し、には作用しない線形演算子なので、左辺は

(3)

この減少は、

と解く場合に特に有効である。 “>

(4)

ここで、上記の演算により、

(5)

そして、これによりは特定の積分形式

(6)

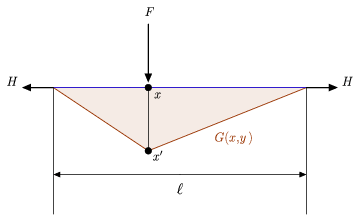
上の図は、グリーン関数の直感的な物理解釈と、上記の定義と比較できる比較的簡単な関連微分方程式を示しています（Hartmann 2013）。 特に、長さの張ったロープを2つの壁の間に吊り下げ、その両端に同じ水平力をかけ、ロープのある内部点に横荷重をかけて固定した状態を示しています。 たわんだロープのに対応する点をx^’とし、下向きの力が一定、例えばとし、ロープのたわみをとすると、たわんだロープは、に対応する点であり、x^’は、たわんだロープ上のに対応する点である。 この物理系に対応するのは、

(7)

for with という微分方程式である。 は、その解 とグリーン関数 の両方を明示的に書くことができる単純な系である。

(8)

and

(9)

それぞれになります。 上図に示されるように、変位したロープは上記ので与えられる区分的線形形式を持つので、この系に関連するグリーン関数は力の適用に対応する水平ロープの作用を表しているという主張を裏付ける。

引数の組 を取ったグリーン関数は2点グリーン関数と呼ばれることもある。 これは多体論の分野で特に重要な多点グリーン関数と対照的である。

上で定義した2点関数の初歩的な例として、電荷密度がである電荷分布が生成するポテンシャルを求める問題を考えてみましょう。 ここで、電荷 の各要素によって生じる における電位にポアソン方程式とクーロンの法則を適用すると、

(10)

が成立する。 の領域で、ある条件下で、. 右辺はをに変換する積分演算子として見ることができるので、この解をグリーン関数は

(11)

で、解は書き直される。

(12)

(Arfken 2012)…と書き直すことができる。

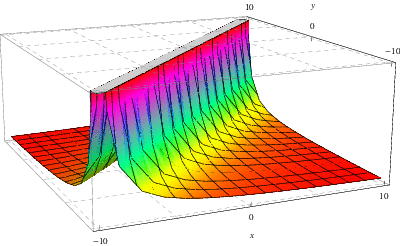
上図は、ここで上述した–方程式の解に付随するグリーン関数を示しています。 と , それぞれ を -, それぞれ -, 軸上にプロットしたものである。

様々な微分方程式に対応するグリーン関数のある程度包括的なリストは Kevin Cole (Cole 2000) によってオンラインで維持されています。

グリーン関数について書かれた多数の文献のために、いくつかの異なる表記や定義が現れるかもしれません。そのいくつかは上記のものとは局所的に異なりますが、一般的には結果の重要な特性には影響しません。 例えば、上の例で示したように、変数 と をベクトル と で表し、1より大きい に対して の要素であることを強調したい著者もいる (Arfken 1985)。 また、が

(13)

が、この純粋に物理的な考察は根本の数学に影響しないため、この観点は一般に見落とされがちである。 グリーン関数の表記は他にもいくつか知られており、の代わりに小文字のを使用したり（Stakgold 1979）、コンマの代わりに縦線を入れたりしている例もあります。 (Duffy 2001)。

他の例では、文献は、それらが提示されているコンテキストと密接に接続されている定義を提示します。 例えば、特殊な領域上に存在する、非常に特殊な微分演算子 と関連する、あるいは正確な境界条件を満たすなど、ある種の条件を満たすグリーン関数を定義している著者もいます。 このような最も一般的な例は、例えば, Omega×Omega” class=”alignright”> の点 、 の境界 にあるすべての点 に対して と定義する (Speck 2011)． この特定の定義は、一般化されたポアソン方程式の解に対応する積分カーネルを提示し、したがって、より一般的な設定に適応されたときに明らかな制限に直面することになる。 一方、このような例にも利点がないわけではない。 例えば、上記の一般化ポアソンの例では、そのようなグリーン関数はそれぞれ

(14)

ここで と 正規ラプラシアンは (Hartman 2013) です。 このような状況では、は基礎となる微分方程式の基本解、はその正規解として知られ、そのためとはそれぞれの基本部と正規部ということもある。

一般的なグリーン関数のいくつかの基本的な性質は、その定義から直ちに（あるいはほとんどそのように）導かれ、すべての特定のインスタンスに引き継がれる。 例えば、演算子 のカーネルが自明でない場合、1つの演算子に関連するグリーン関数が複数存在する可能性があるため、「あの」グリーン関数と呼ぶときには注意が必要である。 グリーン関数はその2つの引数において、

(15)

ここで、は方程式

(16)

ここで、はの随伴値である。 この事実の直接的な帰結の一つは、自己共役演算子について、は対称的である：

(17)

この恒等式はしばしば相互原理と呼ばれ、物理用語としては、での単位ソースによるでの応答は、での単位力によるでの応答と同じということを述べています (Stakgold 1979)。

あらゆるグリーン関数の本質的な特性は、ある種のソース項に対する任意の微分方程式の解の応答を、ある数の境界条件の存在下で記述する方法を提供することです（Arfken et al.2012）。 グリーン関数は偏微分方程式の理論において、常微分方程式の解におけるフーリエ級数とほぼ同様の役割を果たすと考える著者もいる（Mikula and Kos 2006）。

より抽象的なシナリオでは、グリーン関数の概念に文脈依存した類似概念として多くのものが存在する。 例えば、関数解析では、関数ではなく汎関数に対して抽象的に積分したときに多くの類似した特性を持つ、いわゆる一般化グリーン関数を考えることがしばしば有用である。 実際、このような一般化は、理論的なPDE解析の全く類似した一分野を生み出し、それ自体が多くの研究の焦点となっている

。