ギブスサンプリング

Like like other MCMC methods, ギブスサンプラーは、値が目標分布に収束するマルコフ連鎖を構築します。 ギブスサンプリングは実際、提案が常に受け入れられるメトロポリス・ヘイスティングスアルゴリズムの特定のケースである。

詳しく説明すると、多変量確率分布をサンプリングしたいとする。

注：多変量確率分布は複数の変数の関数（例. 2次元正規分布）です。

後者を直接サンプルする方法は分かりません。 しかし、数学的な都合か、あるいは単なる運で、我々はたまたま条件付き確率を知っている。

ここでギブスサンプリングの登場である。 5089>

まず、確率変数X & Yの初期値を選び、Y=Y⁰が与えられたときのXの条件付き確率分布（p(X|Y⁰)とする）からサンプリングします。 次のステップでは，先ほど計算したX¹を条件とする新たなYの値を標本化する． この手順をさらにn – 1回繰り返し、もう一方の確率変数の現在値を与えて、Xの条件付き確率分布とYの条件付き確率分布から新しいサンプルを交互に引きます。

例で見てみましょう。 次のような事後確率分布と条件付き確率分布があったとします。

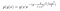
ここで g(y) にはxを含まない項が含まれる。 g(x)はyに依存しないものを含む。

C（正規化定数）の値はわからない。 しかし、条件付き確率分布は分かっている。

注：条件付き確率は実際には正規分布であり、次のように書き換えることができます。

以上の式をもとに、ギブスサンプリングの実装に進みます。 まず、以下のライブラリをインポートします。

import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
sns.set()

事後分布の関数を定義します（C=1とします）。

f = lambda x, y: np.exp(-(x*x*y*y+x*x+y*y-8*x-8*y)/2.)

そして、確率分布をプロットします。

xx = np.linspace(-1, 8, 100)
yy = np.linspace(-1, 8, 100)
xg,yg = np.meshgrid(xx, yy)
z = f(xg.ravel(), yg.ravel())
z2 = z.reshape(xg.shape)
plt.contourf(xg, yg, z2, cmap='BrBG')

さて、ギブスサンプリングを使って確率分布を推定してみます。 前回述べたように、条件付き確率は正規分布です。

以下のブロックでは、muとsigmaの関数を定義し、確率変数X & Yを初期化し、N（反復回数）を設定します。

N = 50000
x = np.zeros(N+1)
y = np.zeros(N+1)
x = 1.
y = 6.
sig = lambda z, i: np.sqrt(1./(1.+z*z))
mu = lambda z, i: 4./(1.+z*z)

ギブスサンプリングのアルゴリズムでステップ実行します。

plt.hist(x, bins=50);
plt.hist(y, bins=50);

plt.contourf(xg, yg, z2, alpha=0.8, cmap='BrBG')
plt.plot(x,y, '.', alpha=0.1)
plt.plot(x,y, c='r', alpha=0.3, lw=1)

見ての通りです。 ギブスサンプリングのアルゴリズムで得られた確率分布は、目標分布によく近似しています。

結論

ギブスサンプリングはモンテカルロ・マルコフチェーン法で、複雑な結合分布を推定するために、各変数の分布から、他の変数の現在値を条件に、繰り返しインスタンスを描画する。 Metropolis-Hastingsアルゴリズムとは対照的に、常に提案を受け入れる。 したがって、ギブスサンプリングははるかに効率的であることができる

。