ガリレオ変換-工学部物理教室
ガリレオ変換は、位置座標、速度、加速度、時間など、いくつかの物理量をある慣性フレームから別のフレームに変換するために使われます。
以上の事実を説明するために、図に示すような二つの参照枠SとS’を考えてみよう。枠sは静止しており、枠s’はX方向に速度vで動いている。 一人は慣性枠x,y,zに対して実験を行っており、もう一人はプライム座標系x’,y’,z’にいる。 プライム座標系は慣性座標系
に対して相対運動しており、点Pで起こる事象を2人の観測者、1人はフレームの原点Oに、もう1人はフレームS’の原点O’にいる観測者によって観測することができるものとする。 t=0において、フレームSとS’の原点OとO’は一致する。
慣性フレームに対する質量の位置をr、プライム座標に対する位置をr’とする。 二つの系の原点はRだけずれている。
……(1.1)
微分をとる
……(1.2)
そして
……….(1.3）
もし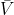
が一定、言い換えればプライム座標の相対運動が均一であれば、
or
従って、慣性フレーム参照の粒子での加速度は、たとえそれらが互いに等速度で相対運動しても同じである。
or
ここでは慣性フレームで観測される物理的相互作用による力、
はプリム座標で測定される同じ力である。 この力は両方の座標系で同じである。 したがって、慣性系に対して一様に運動する系の運動方程式は、慣性系のものと同一である。 慣性系に対して一様に並進するすべての系は同一である。 あるいは運動の第二法則はガリレオ変換のもとで不変である
もちろん上記の議論は、原始座標系の相対運動が光の速度に全く匹敵しない場合にのみ有効である。 もし、この系が光の速度に匹敵する速度で運動するならば、いくつかの複雑な問題が生じるだろう。
もし座標系の原点がt=0, で一致するように選ぶと、
と
これらはGalilean変換と呼ばれるもので、この変換を用いると、
が得られる。
Oから観測したPの座標を(x, y, z, t)、O’から観測した座標を(x’, y’, z’, t’)とする。 フレームSとS’におけるPの座標の関係は
x’ = x – vt、
y’ = y、
z’ = z
である。
Leave a Reply