Una leggera introduzione al problema degli scafi convessi
Gli scafi convessi tendono ad essere utili in molti campi diversi, a volte in modo abbastanza inaspettato. In questo articolo, spiegherò l’idea di base degli scafi convessi 2d e come usare la scansione graham per trovarli. Quindi, se conoscete già la scansione di Graham, allora questo articolo non fa per voi, ma in caso contrario, questo dovrebbe familiarizzarvi con alcuni dei concetti rilevanti.
Il guscio convesso di un insieme di punti è definito come il più piccolo poligono convesso, che racchiude tutti i punti dell’insieme. Convesso significa che il poligono non ha angoli piegati verso l’interno.

I bordi rossi sul poligono di destra racchiudono l’angolo in cui la forma è concava, l’opposto di convessa.
Un modo utile per pensare allo scafo convesso è l’analogia dell’elastico. Supponiamo che i punti dell’insieme siano chiodi che spuntano da una superficie piatta. Immaginate ora cosa accadrebbe se prendeste un elastico e lo allungaste intorno ai chiodi. Cercando di contrarsi alla sua lunghezza originale, l’elastico racchiuderebbe i chiodi, toccando quelli che sporgono più lontano dal centro.
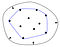
Per rappresentare la carena convessa risultante nel codice, di solito memorizziamo la lista dei punti che reggono questo elastico, cioè la lista dei punti sulla carena convessa.
Nota che abbiamo ancora bisogno di definire cosa dovrebbe accadere se tre punti giacciono sulla stessa linea. Se si immagina che l’elastico abbia un punto in cui tocca uno dei chiodi, ma non si piega affatto, ciò significa che il chiodo si trova su una linea retta tra altri due chiodi. A seconda del problema, potremmo considerare questo chiodo lungo la linea retta come parte dell’uscita, poiché tocca l’elastico. D’altra parte, potremmo anche dire che questo chiodo non dovrebbe far parte dell’output, perché la forma dell’elastico non cambia quando lo rimuoviamo. Questa decisione dipende dal problema su cui state lavorando, e soprattutto se avete un input in cui nessun punto è collineare (questo è spesso il caso nei compiti facili per le competizioni di programmazione) allora potete anche ignorare completamente questo problema.
Trovare lo scafo convesso
Guardando un insieme di punti, l’intuizione umana ci permette di capire rapidamente quali punti hanno la probabilità di toccare lo scafo convesso, e quali saranno più vicini al centro e quindi lontani dallo scafo convesso. Ma tradurre questa intuizione in codice richiede un po’ di lavoro.
Per trovare la carena convessa di un insieme di punti, possiamo usare un algoritmo chiamato Graham Scan, che è considerato uno dei primi algoritmi di geometria computazionale. Usando questo algoritmo, possiamo trovare il sottoinsieme di punti che giacciono sullo scafo convesso, insieme all’ordine in cui questi punti si incontrano quando si gira intorno allo scafo convesso.
L’algoritmo inizia con la ricerca di un punto, che sappiamo giace sicuramente sullo scafo convesso. Il punto con la coordinata y più bassa, per esempio, può essere considerato una scelta sicura. Se esistono più punti alla stessa coordinata y, prendiamo quello che ha la coordinata x più grande (questo funziona anche con altri punti d’angolo, ad esempio prima la x più bassa poi la y più bassa).


Ora, l’idea dell’algoritmo è di camminare intorno a questo array ordinato, determinando per ogni punto, se si trova o meno sullo scafo convesso. Questo significa che per ogni tripla di punti che incontriamo, decidiamo se formano un angolo convesso o concavo. Se l’angolo è concavo, allora sappiamo che il punto centrale di questa tripletta non può trovarsi sullo scafo convesso.
(Si noti che i termini angolo concavo e convesso devono essere usati in relazione all’intero poligono, solo un angolo da solo non può essere convesso o concavo, poiché non ci sarebbe una direzione di riferimento.)
Memorizziamo i punti che giacciono sullo scafo convesso su una pila, in questo modo possiamo aggiungere punti se li raggiungiamo nel nostro percorso intorno ai punti ordinati, e rimuoverli se scopriamo che formano un angolo concavo.
(In senso stretto, dobbiamo accedere ai primi due punti della pila, quindi usiamo invece un std::vector, ma pensiamolo come una specie di pila, perché siamo sempre preoccupati solo della coppia di elementi in alto.)
Correndo la matrice ordinata di punti, aggiungiamo il punto alla pila, e se poi scopriamo che il punto non appartiene allo scafo convesso, lo rimuoviamo.
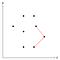
Possiamo misurare se l’angolo corrente si piega verso l’interno o verso l’esterno calcolando il prodotto incrociato e controllando se è positivo o negativo. La figura qui sopra mostra una terzina di punti in cui l’angolo che formano è convesso, quindi quello centrale di questi tre punti rimane per ora sulla pila.
Passando al punto successivo, continuiamo a fare la stessa cosa: controllare se l’angolo è convesso e se non lo è, rimuovere il punto. Poi continuiamo aggiungendo il punto successivo e ripetiamo.
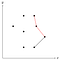
Questo angolo segnato in rosso è concavo, quindi eliminiamo il punto centrale dalla pila perché non può far parte dello scafo convesso.
Come facciamo a sapere che questo ci darà la risposta corretta?
Scrivere una dimostrazione rigorosa è fuori dallo scopo di questo articolo, ma posso scrivere le idee di base. Vi incoraggio, comunque, ad andare avanti e cercare di colmare le lacune!
Siccome abbiamo calcolato il prodotto incrociato in ogni angolo, sappiamo per certo che stiamo ottenendo un poligono convesso. Ora dobbiamo solo dimostrare che questo poligono convesso racchiude davvero tutti i punti.
(In realtà, avremmo anche bisogno di dimostrare che questo è il più piccolo poligono convesso possibile che soddisfa queste condizioni, ma questo segue abbastanza facilmente dal fatto che i punti angolari del nostro poligono convesso sono un sottoinsieme dell’insieme originale di punti.)
Supponiamo che esista un punto P fuori dal poligono che abbiamo appena trovato.
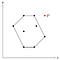
Siccome ogni punto è stato aggiunto alla pila una volta, sappiamo che P è stato rimosso dalla pila ad un certo punto. Questo significa che P, insieme ai suoi punti vicini, chiamiamoli O e Q, ha formato un angolo concavo.
Siccome O e Q stanno dentro il poligono (o sul suo bordo), anche P dovrebbe stare dentro il bordo, perché il poligono è convesso e l’angolo che O e Q formano con P è concavo rispetto al poligono.
Quindi abbiamo trovato una contraddizione, che significa che un tale punto P non può esistere.
Implementazione
L’implementazione qui fornita ha una funzione convex_hull, che prende un std::vector che contiene i punti come std::pairs di ints e restituisce un altro std::vector che contiene i punti che stanno sul guscio convesso.
Analisi del tempo di esecuzione e della memoria
È sempre utile pensare agli algoritmi di complessità in termini di notazione Big-O, che non spiegherò qui, perché Michael Olorunnisola ha già fatto un lavoro molto migliore di me per spiegarlo:
Eseguire i punti richiede inizialmente tempo O(n log n), ma dopo, ogni passo può essere calcolato in tempo costante. Ogni punto viene aggiunto e rimosso dallo stack al massimo una volta, questo significa che il runtime nel caso peggiore sta in O(n log n).
L’uso della memoria, che sta in O(n) al momento, potrebbe essere ottimizzato eliminando la necessità dello stack ed eseguendo le operazioni direttamente sull’array di input. Potremmo spostare i punti che si trovano sullo scafo convesso all’inizio dell’array di input e sistemarli nel giusto ordine, e gli altri punti verrebbero spostati nel resto dell’array. La funzione potrebbe quindi restituire solo una singola variabile intera che denota la quantità di punti nell’array che giacciono sullo scafo convesso. Questo, naturalmente, ha il rovescio della medaglia, che la funzione diventa molto più complicata, quindi ve lo sconsiglio, a meno che non stiate codificando per sistemi embedded o abbiate problemi di memoria altrettanto restrittivi. Per la maggior parte delle situazioni, il compromesso probabilità di bug/risparmio di memoria non vale la pena.
Altri algoritmi
Un’alternativa al Graham Scan è l’algoritmo di Chan, che si basa effettivamente sulla stessa idea ma è più facile da implementare. Ha senso però capire prima come funziona il Graham Scan.
Se vi sentite davvero fantasiosi e volete affrontare il problema in tre dimensioni, date un’occhiata all’algoritmo di Preparata e Hong introdotto nel loro articolo del 1977 “Convex Hulls of Finite Sets of Points in Two and Three Dimensions”.
Leave a Reply