Una breve introduzione alla privacy differenziale

Georgiano

Follow

31 agosto, 2018 – 10 min read

Aaruran Elamurugaiyan

La privacy può essere quantificata. Meglio ancora, possiamo classificare le strategie che preservano la privacy e dire quale è più efficace. Meglio ancora, possiamo progettare strategie che sono robuste anche contro gli hacker che hanno informazioni ausiliarie. E come se non bastasse, possiamo fare tutte queste cose contemporaneamente. Queste soluzioni, e altre ancora, risiedono in una teoria probabilistica chiamata privacy differenziale.

Ecco il contesto. Stiamo curando (o gestendo) un database sensibile e vorremmo rilasciare alcune statistiche di questi dati al pubblico. Tuttavia, dobbiamo assicurarci che sia impossibile per un avversario di reingegnerizzare i dati sensibili da ciò che abbiamo rilasciato. Un avversario in questo caso è una parte con l’intenzione di rivelare, o di apprendere, almeno alcuni dei nostri dati sensibili. La privacy differenziale può risolvere i problemi che sorgono quando questi tre ingredienti – dati sensibili, curatori che devono rilasciare statistiche, e avversari che vogliono recuperare i dati sensibili – sono presenti (vedi Figura 1). Questo reverse-engineering è un tipo di violazione della privacy.

Ma quanto è difficile violare la privacy? Non basterebbe rendere anonimi i dati? Se si hanno informazioni ausiliarie da altre fonti di dati, l’anonimizzazione non è sufficiente. Per esempio, nel 2007, Netflix ha rilasciato un set di dati delle loro valutazioni degli utenti come parte di una competizione per vedere se qualcuno può superare il loro algoritmo di filtraggio collaborativo. Il dataset non conteneva informazioni di identificazione personale, ma i ricercatori sono stati comunque in grado di violare la privacy; hanno recuperato il 99% di tutte le informazioni personali che sono state rimosse dal dataset. In questo caso, i ricercatori hanno violato la privacy utilizzando informazioni ausiliarie da IMDB.

Come ci si può difendere da un avversario che ha un aiuto sconosciuto, e possibilmente illimitato, dal mondo esterno? La privacy differenziale offre una soluzione. Gli algoritmi a privacy differenziale sono resistenti agli attacchi adattativi che utilizzano informazioni ausiliarie. Questi algoritmi si basano sull’incorporazione di rumore casuale nel mix in modo che tutto ciò che un avversario riceve diventa rumoroso e impreciso, e quindi è molto più difficile violare la privacy (se è fattibile).

Conteggio rumoroso

Guardiamo un semplice esempio di iniezione di rumore. Supponiamo di gestire un database di rating di credito (riassunto dalla tabella 1).

Per questo esempio, supponiamo che l’avversario voglia conoscere il numero di persone che hanno un cattivo rating (che è 3). I dati sono sensibili, quindi non possiamo rivelare la verità di base. Invece useremo un algoritmo che restituisce la verità di base, N = 3, più un po’ di rumore casuale. Questa idea di base (aggiungere rumore casuale alla verità di base) è la chiave della privacy differenziale. Diciamo che scegliamo un numero casuale L da una distribuzione Laplace centrata su zero con deviazione standard di 2. Restituiamo N+L. Spiegheremo la scelta della deviazione standard tra qualche paragrafo. (Se non avete sentito parlare della distribuzione di Laplace, guardate la figura 2). Chiameremo questo algoritmo “conteggio rumoroso”.

Se dobbiamo riportare una risposta insensata e rumorosa, qual è lo scopo di questo algoritmo? La risposta è che ci permette di trovare un equilibrio tra utilità e privacy. Vogliamo che il pubblico in generale ottenga una certa utilità dal nostro database, senza esporre alcun dato sensibile a un possibile avversario.

Cosa riceverebbe effettivamente l’avversario? Le risposte sono riportate nella Tabella 2.

La prima risposta che l’avversario riceve è vicina, ma non uguale alla verità di base. In questo senso, l’avversario è ingannato, l’utilità è fornita e la privacy è protetta. Ma dopo molteplici tentativi, sarà in grado di stimare la verità di base. Questa “stima da interrogazioni ripetute” è uno dei limiti fondamentali della privacy differenziale. Se l’avversario può fare un numero sufficiente di interrogazioni a un database differentemente privato, può ancora stimare i dati sensibili. In altre parole, con sempre più query, la privacy viene violata. La tabella 2 dimostra empiricamente questa violazione della privacy. Tuttavia, come si può vedere, l’intervallo di confidenza del 90% da queste 5 query è abbastanza ampio; la stima non è ancora molto accurata.

Quanto può essere accurata questa stima? Date un’occhiata alla Figura 3 dove abbiamo eseguito una simulazione diverse volte e tracciato i risultati.

Ogni linea verticale illustra la larghezza di un intervallo di confidenza del 95%, e i punti indicano la media dei dati campionati dall’avversario. Si noti che questi grafici hanno un asse orizzontale logaritmico, e che il rumore è tratto da variabili casuali di Laplace indipendenti e identicamente distribuite. Nel complesso, la media è più rumorosa con un minor numero di interrogazioni (poiché le dimensioni del campione sono piccole). Come previsto, gli intervalli di confidenza diventano più stretti man mano che l’avversario fa più interrogazioni (poiché la dimensione del campione aumenta e il rumore ha una media pari a zero). Solo dall’ispezione del grafico, possiamo vedere che ci vogliono circa 50 interrogazioni per fare una stima decente.

Flettiamo su questo esempio. Innanzitutto, aggiungendo del rumore casuale, abbiamo reso più difficile per un avversario violare la privacy. In secondo luogo, la strategia di occultamento che abbiamo impiegato era semplice da implementare e comprendere. Sfortunatamente, con sempre più query, l’avversario è stato in grado di approssimare il vero conteggio.

Se aumentiamo la varianza del rumore aggiunto, possiamo difendere meglio i nostri dati, ma non possiamo semplicemente aggiungere qualsiasi rumore di Laplace a una funzione che vogliamo nascondere. La ragione è che la quantità di rumore che dobbiamo aggiungere dipende dalla sensibilità della funzione, e ogni funzione ha la sua sensibilità. In particolare, la funzione di conteggio ha una sensibilità di 1. Diamo un’occhiata a cosa significa sensibilità in questo contesto.

La sensibilità e il meccanismo di Laplace

Per una funzione:

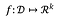
la sensibilità di f è:

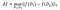
sui set di dati D₁, D₂ che differiscono al massimo su un elemento .

La definizione di cui sopra è abbastanza matematica, ma non è così male come sembra. In parole povere, la sensibilità di una funzione è la più grande differenza possibile che una riga può avere sul risultato di quella funzione, per qualsiasi dataset. Per esempio, nel nostro set di dati giocattolo, il conteggio del numero di righe ha una sensibilità di 1, perché l’aggiunta o la rimozione di una singola riga da qualsiasi set di dati cambierà il conteggio al massimo di 1.

Come altro esempio, supponiamo di pensare a “conteggio arrotondato a un multiplo di 5”. Questa funzione ha una sensibilità di 5, e possiamo dimostrarlo abbastanza facilmente. Se abbiamo due insiemi di dati di dimensione 10 e 11, differiscono in una riga, ma i “conteggi arrotondati a un multiplo di 5” sono rispettivamente 10 e 15. Infatti, cinque è la più grande differenza possibile che questa funzione di esempio può produrre. Pertanto, la sua sensibilità è 5.

Calcolare la sensibilità per una funzione arbitraria è difficile. Una notevole quantità di sforzi di ricerca viene spesa per stimare le sensibilità, migliorare le stime della sensibilità e aggirare il calcolo della sensibilità. La nostra strategia di conteggio rumoroso utilizza un algoritmo chiamato meccanismo di Laplace, che a sua volta si basa sulla sensibilità della funzione che oscura. Nell’algoritmo 1, abbiamo un’implementazione ingenua dello pseudocodice del meccanismo di Laplace .

Algoritmo 1

Input: Funzione F, Input X, Livello di privacy ϵ
Output: Una risposta rumorosa
Computa F (X)
Computa la sensibilità di F: S
Disegna il rumore L da una distribuzione Laplace con varianza:

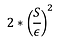
Risulta F(X) + L

Più grande è la sensibilità S, più rumorosa sarà la risposta. Il conteggio ha solo una sensibilità di 1, quindi non abbiamo bisogno di aggiungere molto rumore per preservare la privacy.

Nota che il meccanismo di Laplace nell’algoritmo 1 consuma un parametro epsilon. Ci riferiremo a questa quantità come alla perdita di privacy del meccanismo e fa parte della definizione più centrale nel campo della privacy differenziale: privacy epsilon-differenziale. Per illustrare, se ricordiamo il nostro esempio precedente e usiamo un po’ di algebra, possiamo vedere che il nostro meccanismo di conteggio rumoroso ha una privacy epsilon-differenziale, con un epsilon di 0,707. Regolando epsilon, controlliamo la rumorosità del nostro conteggio rumoroso. Scegliere un epsilon più piccolo produce risultati più rumorosi e migliori garanzie di privacy. Come riferimento, Apple usa un epsilon di 2 nella correzione automatica differenzialmente privata della sua tastiera.

La quantità epsilon è il modo in cui la privacy differenziale può fornire confronti rigorosi tra diverse strategie. La definizione formale della privacy epsilon-differenziale è un po’ più coinvolta matematicamente, quindi l’ho intenzionalmente omessa da questo post del blog. Potete leggerne di più nell’indagine di Dwork sulla privacy differenziale.

Come ricorderete, l’esempio di conteggio rumoroso aveva un epsilon di 0,707, che è abbastanza piccolo. Ma abbiamo ancora violato la privacy dopo 50 query. Perché? Perché con l’aumento delle query, il budget di privacy cresce, e quindi la garanzia di privacy è peggiore.

Il budget di privacy

In generale, le perdite di privacy si accumulano. Quando due risposte vengono restituite ad un avversario, la perdita totale di privacy è due volte più grande, e la garanzia di privacy è la metà più forte. Questa proprietà cumulativa è una conseguenza del teorema di composizione. In sostanza, con ogni nuova query, vengono rilasciate informazioni aggiuntive sui dati sensibili. Quindi, il teorema di composizione ha una visione pessimistica e assume lo scenario peggiore: la stessa quantità di perdita avviene con ogni nuova risposta. Per forti garanzie di privacy, vogliamo che la perdita di privacy sia piccola. Così nel nostro esempio in cui abbiamo una perdita di privacy di trentacinque (dopo 50 richieste al nostro meccanismo di conteggio rumoroso di Laplace), la corrispondente garanzia di privacy è fragile.

Come funziona la privacy differenziale se la perdita di privacy cresce così rapidamente? Per assicurare una garanzia di privacy significativa, i curatori dei dati possono imporre una perdita massima di privacy. Se il numero di richieste supera la soglia, allora la garanzia di privacy diventa troppo debole e il curatore smette di rispondere alle richieste. La massima perdita di privacy è chiamata privacy budget. Possiamo pensare ad ogni richiesta come ad una “spesa” per la privacy che comporta una perdita incrementale di privacy. La strategia di utilizzare budget, spese e perdite è opportunamente conosciuta come privacy accounting.

Privacy accounting è una strategia efficace per calcolare la perdita di privacy dopo query multiple, ma può ancora incorporare il teorema di composizione. Come notato in precedenza, il teorema di composizione presuppone lo scenario peggiore. In altre parole, esistono alternative migliori.

Deep Learning

Deep learning è un sottocampo del machine learning, che riguarda l’addestramento di reti neurali profonde (DNN) per stimare funzioni sconosciute. (Ad alto livello, una DNN è una sequenza di trasformazioni affini e non lineari che mappano uno spazio n-dimensionale in uno spazio m-dimensionale). Le sue applicazioni sono molto diffuse, e non c’è bisogno di ripeterle qui. Esploreremo privatamente come addestrare una rete neurale profonda.

Le reti neurali profonde sono tipicamente addestrate usando una variante della discesa del gradiente stocastico (SGD). Abadi et al. hanno inventato una versione che preserva la privacy di questo popolare algoritmo, comunemente chiamato “SGD privato” (o PSGD). La figura 4 illustra la potenza della loro nuova tecnica. Abadi et al. hanno inventato un nuovo approccio: il contabile a momenti. L’idea di base dietro il contabile dei momenti è quella di accumulare la spesa per la privacy inquadrando la perdita di privacy come una variabile casuale, e utilizzando le sue funzioni generatrici di momenti per comprendere meglio la distribuzione di quella variabile (da qui il nome) . I dettagli tecnici completi sono al di fuori dello scopo di un post introduttivo del blog, ma vi invitiamo a leggere l’articolo originale per saperne di più.

Pensieri finali

Abbiamo esaminato la teoria della privacy differenziale e visto come può essere usata per quantificare la privacy. Gli esempi in questo post mostrano come le idee fondamentali possono essere applicate e la connessione tra applicazione e teoria. È importante ricordare che le garanzie di privacy si deteriorano con l’uso ripetuto, quindi vale la pena pensare a come mitigare questo fenomeno, sia con il privacy budgeting che con altre strategie. Potete indagare sul deterioramento cliccando su questa frase e ripetendo i nostri esperimenti. Ci sono ancora molte domande senza risposta qui e una ricchezza di letteratura da esplorare – vedi i riferimenti qui sotto. Vi incoraggiamo a leggere ulteriormente.

Cynthia Dwork. Privacy differenziale: Una rassegna di risultati. International Conference on Theory and Applications of Models of Computation, 2008.

Wikipedia Contributors. Distribuzione di Laplace, luglio 2018.

Aaruran Elamurugaiyan. Plot che dimostrano l’errore standard delle risposte differentemente private sul numero di query., agosto 2018.

Benjamin I. P. Rubinstein e Francesco Alda. Privacy differenziale casuale senza dolore con il campionamento della sensibilità. In 34th International Conference on Machine Learning (ICML’2017) , 2017.

Cynthia Dwork e Aaron Roth. Le basi algoritmiche della privacy differenziale . Ora Publ., 2014.

Martin Abadi, Andy Chu, Ian Goodfellow, H. Brendan Mcmahan, Ilya Mironov, Kunal Talwar e Li Zhang. Apprendimento profondo con privacy differenziale. Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security – CCS16 , 2016.

Frank D. McSherry. Query integrate alla privacy: Una piattaforma estensibile per l’analisi dei dati che rispetta la privacy. In Proceedings of the 2009 ACM SIGMOD International Conference on Management of Data , SIGMOD ’09, pagine 19-30, New York, NY, USA, 2009. ACM.

Collaboratori di Wikipedia. Apprendimento profondo, agosto 2018.