Test Friedman in SPSS Statistics
SPSS Statistics
SPSS Statistics Output per il Test Friedman
SPSS Statistics genererà due o tre tabelle, a seconda che tu abbia scelto di far generare i descrittivi e/o i quartili oltre a eseguire il test Friedman.
Tabella delle statistiche descrittive
La tabella delle statistiche descrittive sarà prodotta se hai selezionato l’opzione quartili:
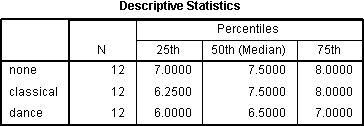
Pubblicato con il permesso scritto di SPSS Statistics, IBM Corporation.
Questa è una tabella molto utile perché può essere usata per presentare statistiche descrittive nella tua sezione dei risultati per ciascuno dei punti di tempo o condizioni (a seconda del disegno dello studio) per la tua variabile dipendente. Questa utilità sarà presentata nella sezione “Riportare l’output” più avanti.
Tabella dei ranghi
La tabella dei ranghi mostra il rango medio per ciascuno dei gruppi correlati, come mostrato di seguito:

Pubblicato con il permesso scritto di SPSS Statistics, IBM Corporation.
Il test di Friedman confronta i ranghi medi tra i gruppi correlati e indica come i gruppi differiscono, ed è incluso per questo motivo. Tuttavia, non è molto probabile che riportiate effettivamente questi valori nella vostra sezione dei risultati, ma molto probabilmente riporterete il valore mediano per ogni gruppo correlato.
Tabella delle statistiche del test
La tabella delle statistiche del test vi informa del risultato effettivo del test di Friedman, e se c’era una differenza complessiva statisticamente significativa tra le classifiche medie dei vostri gruppi correlati. Per l’esempio usato in questa guida, la tabella appare come segue:

Pubblicato con il permesso scritto di SPSS Statistics, IBM Corporation.
La tabella sopra fornisce il valore statistico del test (χ2) (“Chi-square”), i gradi di libertà (“df”) e il livello di significatività (“Asymp. Sig.”), che è tutto ciò di cui abbiamo bisogno per riportare il risultato del test Friedman. Dal nostro esempio, possiamo vedere che c’è una differenza complessiva statisticamente significativa tra i ranghi medi dei gruppi correlati. È importante notare che il test di Friedman è un test omnibus, come la sua alternativa parametrica; cioè, vi dice se ci sono differenze complessive, ma non individua quali gruppi in particolare differiscono tra loro. Per fare questo è necessario eseguire test post hoc, che saranno discussi dopo la prossima sezione.
StatisticheSPSS
Riportare il risultato del test di Friedman (senza test post hoc)
Puoi riportare il risultato del test di Friedman come segue:
- Generale
C’era una differenza statisticamente significativa nello sforzo percepito a seconda del tipo di musica ascoltata durante la corsa, χ2(2) = 7.600, p = 0,022.
Potresti anche includere i valori mediani per ciascuno dei gruppi correlati. Tuttavia, a questo punto, sapete solo che ci sono differenze da qualche parte tra i gruppi correlati, ma non sapete esattamente dove si trovano queste differenze. Ricorda però che se il risultato del tuo test di Friedman non è statisticamente significativo, non dovresti eseguire test post hoc.
Test post hoc
Per esaminare dove si verificano effettivamente le differenze, è necessario eseguire test Wilcoxon signed-rank separati sulle diverse combinazioni di gruppi correlati. Quindi, in questo esempio, dovreste confrontare le seguenti combinazioni:
- Nessuno a Classico.
- Nessuno a Danza.
- Classico a Danza.
È necessario utilizzare una correzione di Bonferroni sui risultati ottenuti dai test di Wilcoxon perché state facendo confronti multipli, il che rende più probabile dichiarare un risultato significativo quando non dovreste (un errore di tipo I). Fortunatamente, l’aggiustamento Bonferroni è molto facile da calcolare: basta prendere il livello di significatività che stavate usando inizialmente (in questo caso, 0.05) e dividerlo per il numero di test che state eseguendo. Quindi, in questo esempio, abbiamo un nuovo livello di significatività di 0,05/3 = 0,017. Questo significa che se il valore p è maggiore di 0,017, non abbiamo un risultato statisticamente significativo.
Eseguendo questi test (vedi come con la nostra guida al test Wilcoxon signed-rank) sui risultati di questo esempio, si ottiene il seguente risultato:

Pubblicato con il permesso scritto di SPSS Statistics, IBM Corporation.
Questa tabella mostra l’output del test Wilcoxon signed-rank su ciascuna delle nostre combinazioni. È importante notare che i valori di significatività non sono stati aggiustati in SPSS Statistics per compensare i confronti multipli – è necessario confrontare manualmente i valori di significatività prodotti da SPSS Statistics con il livello di significatività aggiustato da Bonferroni che avete calcolato. Possiamo vedere che al livello di significatività p < 0,017, solo lo sforzo percepito tra nessuna musica e la danza (dance-none, p = 0,008) era statisticamente diverso.
StatisticheSPSS
Relazione dei risultati del test di Friedman (con test post hoc)
Puoi riportare i risultati del test di Friedman con test post hoc come segue:
- Generale
C’era una differenza statisticamente significativa nello sforzo percepito a seconda di quale tipo di musica veniva ascoltata durante la corsa, χ2(2) = 7.600, p = 0.022. L’analisi post hoc con i test Wilcoxon signed-rank è stata condotta con una correzione di Bonferroni applicata, ottenendo un livello di significatività fissato a p < 0,017. I livelli mediani (IQR) di sforzo percepito per la prova di corsa senza musica, classica e con musica da ballo erano rispettivamente 7,5 (da 7 a 8), 7,5 (da 6,25 a 8) e 6,5 (da 6 a 7). Non ci sono state differenze significative tra le prove di corsa senza musica e con musica classica (Z = -0,061, p = 0,952) o tra le prove di corsa con musica classica e con musica da ballo (Z = -1,811, p = 0,070), nonostante una riduzione complessiva dello sforzo percepito nelle prove di corsa con danza rispetto alla classica. Tuttavia, c’era una riduzione statisticamente significativa dello sforzo percepito nella prova di musica da ballo rispetto a nessuna prova di musica (Z = -2.636, p = 0.008).
Leave a Reply