Risonanza di Helmholtz
- Analisi della risonanza di Helmholtz
- Risonanza, impedenza, dipendenza dalla fase e dalla frequenza
- Complicazioni sulla lunghezza
- Risonanze di Helmholtz e chitarre
Analisi della risonanza di Helmholtz
Ora diventiamo quantitativi: Prima di tutto, assumiamo che la lunghezza d’onda del suono prodotto sia molto più lunga delle dimensioni del risonatore. Per le bottiglie nell’animazione all’inizio di questa pagina, le lunghezze d’onda sono rispettivamente 180 e 74 cm, quindi questa approssimazione è abbastanza buona, ma vale la pena controllare ogni volta che si inizia a descrivere qualcosa come un oscillatore di Helmholtz. La conseguenza di questa approssimazione è che possiamo trascurare le variazioni di pressione all’interno del volume del contenitore: l’oscillazione di pressione avrà la stessa fase ovunque all’interno del contenitore.
Lasciamo che l’aria nel collo abbia una lunghezza effettiva L e una sezione trasversale S. La sua massa è quindi SL volte la densità dell’aria ρ. (Alcune complicazioni sulla lunghezza effettiva sono discusse alla fine di questa pagina). Se questo ‘tappo’ d’aria scende una piccola distanza x nella bottiglia, comprime l’aria nel contenitore in modo che l’aria che prima occupava il volume V ora ha volume V – Sx. Di conseguenza, la pressione di quell’aria sale dalla pressione atmosferica PA a un valore più alto PA + p.
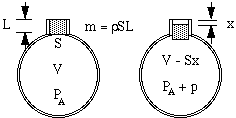
Ora si potrebbe pensare che l’aumento di pressione sarebbe semplicemente proporzionale alla diminuzione del volume. Sarebbe così se la compressione avvenisse così lentamente che la temperatura non cambiasse. Nelle vibrazioni che danno origine al suono, tuttavia, i cambiamenti sono veloci e quindi la temperatura aumenta alla compressione, dando un cambiamento più grande nella pressione. Tecnicamente sono adiabatiche, il che significa che il calore non ha tempo per muoversi, e l’equazione risultante coinvolge una costante γ, il rapporto dei calori specifici, che è circa 1,4 per l’aria. (Come risultato, il cambiamento di pressione p prodotto da un piccolo cambiamento di volume ΔV è solo
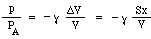
Ora la massa m è spostata dalla differenza di pressione tra la parte superiore e inferiore del collo, cioè una forza netta pS, quindi scriviamo la legge di Newton per l’accelerazione a:
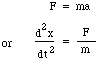
sostituendo F e m si ottiene: 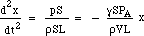
Quindi la forza di ripristino è proporzionale allo spostamento. Questa è la condizione per il moto armonico semplice, e ha una frequenza che è 1/2π volte la radice quadrata della costante di proporzionalità, quindi
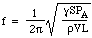
Ora la velocità c del suono in aria è determinata dalla densità, dalla pressione e dal rapporto dei calori specifici, quindi possiamo scrivere:
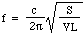
Mettiamo qualche numero: per una bottiglia da 1 litro, con S = 3 centimetri quadrati e L = 5 centimetri, la frequenza è 130 Hz, che è circa il Do sotto il Do centrale (vedi note). Quindi la lunghezza d’onda è 2,6 metri, che è molto più grande della bottiglia. Questo giustifica, post hoc, l’ipotesi fatta all’inizio della derivazione.
Resonanza, impedenza, dipendenza dalla fase e dalla frequenza
Questa sezione può essere letta da sola, ma se vuoi un background più dettagliato, vedi Oscillazioni, Oscillazioni forzate e Conformità acustica, inerzia e impedenza.
Torniamo alla rappresentazione meccanica e guardiamo il risonatore di Helmholtz dall’esterno, come mostrato nel primo schema: stiamo spingendo con una forza oscillatoria F, con frequenza f , la massa m (l’aria nel collo del risonatore), che è appoggiata sulla molla (l’aria racchiusa) con costante elastica k, la cui altra estremità è fissa (l’aria nel risonatore non può uscire). Non realisticamente, trascureremo la gravità e l’attrito (per ora).
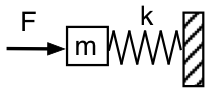
La forza richiesta per accelerare la massa è proporzionale all’accelerazione e quindi proporzionale a f2. A frequenza sufficientemente bassa, la forza richiesta per accelerare la massa è trascurabile, quindi F deve solo comprimere ed estendere la molla. Quindi, in quel limite, la forza applicata F = +kx. (La forza della molla è -kx.) L’impedenza meccanica del sistema a questa bassa frequenza è conforme o a molla. Acusticamente, sembra una cedevolezza acustica: spingiamo la massa d’aria nel collo e comprimiamo l’aria nel risonatore. La forza applicata F a destra è in fase con x misurata a destra, quindi è 90° dietro la velocità e la pressione applicata è 90° dietro il flusso acustico nel risonatore.
Ricordate che f2 dipende dall’accelerazione. Quindi, a frequenza sufficientemente alta, la forza della molla è trascurabile rispetto a quella che accelera la massa. Quindi F è in fase con l’accelerazione, il che la pone 90° davanti alla velocità. Acusticamente, la pressione applicata è 90° avanti rispetto al flusso acustico nel risonatore. È un’inerzia meccanica o acustica.
Alla frequenza di risonanza (sempre parlando dello schizzo sopra), l’ampiezza può essere grande per una forza molto piccola. Così alla risonanza, l’impedenza è molto bassa, se vista dalla forza applicata alla massa dall’esterno (lo schema sopra). Alla risonanza, c’è il massimo flusso in entrata e in uscita dal risonatore.
Ora consideriamo cosa succede se guardiamo la pressione all’interno del risonatore (lontano dal collo). Qui stiamo guardando la forza sulla molla, quindi il nostro analogo meccanico assomiglia a questo schema.
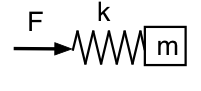
Questa volta, bassa frequenza significa che la forza può essere piccola per una data ampiezza: la molla e la massa si muovono insieme come una massa, e il sistema questa volta sembra inerte a bassa frequenza. Ad alta frequenza, la massa difficilmente si muove, e il sistema è simile a una molla o cedevole. Quindi le relazioni di fase sono opposte a quelle che avevamo prima: a bassa f, p conduce U di 90°; ad alta f, p ritarda U di 90°.
Complicazioni che coinvolgono la lunghezza effettiva
Il primo diagramma in questa pagina disegna il “tappo” d’aria come se fosse un cilindro che termina ordinatamente alle due estremità del collo della bottiglia. Questo è troppo semplificato. In pratica, un volume extra sia all’interno che all’esterno si muove con l’aria nel collo – come suggerito nell’animazione sopra. La lunghezza extra che dovrebbe essere aggiunta alla lunghezza geometrica del collo è tipicamente (e molto approssimativamente) di 0,6 volte il raggio all’estremità esterna, e un raggio all’estremità interna).
|
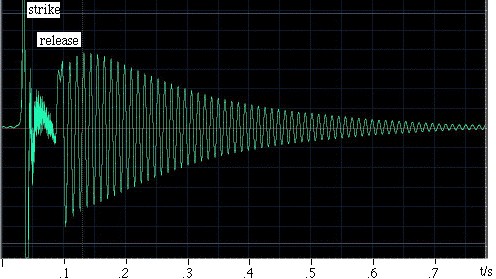
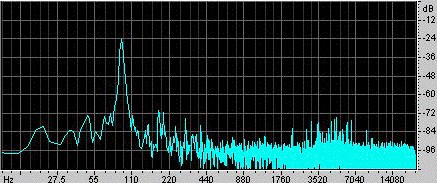
Un esempio. Ra Inta ha fatto questo esempio. Ha preso un risonatore sferico di Helmholtz con un volume di 0,00292 m3 e un collo cilindrico di lunghezza 0,080 m e sezione trasversale 0,00083 m2. Per eccitarlo, lo colpisce con il palmo della mano e poi lo rilascia. Un microfono all’interno del risonatore registra il suono, che è mostrato nell’oscillogramma a sinistra. Si può vedere che la mano sigilla il risonatore per poco meno di 0,1 s, e che durante questo tempo le oscillazioni sono più deboli e di frequenza relativamente alta. Una volta che la mano viene rilasciata, si stabilisce un’oscillazione, che gradualmente muore via via che perde energia attraverso la resistenza viscosa e turbolenta, e anche attraverso la radiazione sonora. Un esame ravvicinato mostra che la frequenza aumenta leggermente quando la mano si allontana dall’estremità aperta, perché questa mano limita l’angolo solido disponibile per la radiazione e quindi aumenta l’effetto finale (o correzione finale). La lunghezza del collo è aumentata di un effetto finale baffled e uno unbaffled, dandogli una lunghezza effettiva di 0,105 m. Con una velocità del suono di 343 m/s, l’espressione sopra dà una frequenza di risonanza di 90 Hz. |
|
Risonanze di Helmholtz e chitarre
* Ho detto sopra che l’aria nel corpo di una chitarra si comporta quasi come un oscillatore di Helmholtz. Questo caso è complicato perché il corpo può gonfiarsi un po’ quando la pressione dell’aria sale all’interno – e anche perché l’aria ‘nella’ buca della chitarra ha una geometria meno facilmente visualizzabile di quella nel collo di una bottiglia. Infatti, nel caso del corpo della chitarra, la lunghezza della spina d’aria è approssimativamente uguale ai due “effetti finali” all’estremità di un “tubo” che è spesso solo un paio di mm. Gli effetti finali, tuttavia, sono legati e di dimensioni simili al raggio del foro, quindi la massa d’aria è sostanziale. La lunghezza dell’effetto finale di un tubo cilindrico che si apre su un deflettore infinito e piano è 0,85 volte il raggio del tubo. Sebbene la tavola armonica di una chitarra non sia infinita, ci si aspetterebbe un effetto finale simile, e quindi la lunghezza effettiva della “spina” d’aria sarebbe circa 1,7 volte il raggio del foro. (Alcuni costruttori aumentano questo valore fissando un breve tubo sotto la buca, con raggio uguale).
Un paio di persone hanno scritto chiedendo quanto grande dovrebbe essere la buca per un dato strumento. Bene, possiamo usare l’equazione di cui sopra per iniziare a rispondere a questa domanda. Tuttavia, il rigonfiamento del corpo è importante. Questo rende la “molla” dell’aria piuttosto morbida, e quindi abbassa la frequenza. La risonanza puramente Helmholtz può essere studiata mantenendo il volume del corpo costante. Quando si misura questo, una pratica comune è quella di seppellire la chitarra nella sabbia, per impedire il gonfiore o la “respirazione” del corpo. Tuttavia, le chitarre di solito non vengono suonate in questa situazione. Quindi il calcolo di Helmholtz darà una sovrastima della frequenza di risonanza per un corpo reale e flessibile.
Assumiamo una buca sonora circolare con raggio r, quindi S = πr2, e L = 1,7r come spiegato sopra. Quando sostituiamo nell’equazione per la frequenza di Helmholtz, usando c = 340 m/s, otteniamo:
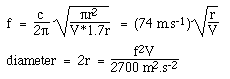
Si noti che stiamo usando unità SI standard: abbiamo usato la velocità del suono in metri e secondi, quindi il volume deve essere in metri cubi e la frequenza in Hertz, per dare una risposta in metri.
È più complicato quando i fori del suono non sono circolari, perché l’effetto finale non è uguale a quello di un cerchio con la stessa area. Il dottorando e liutaio John McLennan sta scrivendo un resoconto di alcune misurazioni su questo, che pubblicheremo presto qui.
Sugli strumenti della famiglia delle chitarre e dei violini, la risonanza di Helmholtz (più il corpo) è spesso vicino o un po’ sotto la frequenza della seconda corda più bassa, intorno al Re su un violino o al Sol-A su una chitarra. Si può ridurre o spostare la frequenza di Helmholtz sostanzialmente coprendo tutto o parte del foro con un pezzo di cartone rigido di forma adeguata. Se poi suonate una nota vicino alla risonanza e poi fate scorrere il cartoncino in modo che copra e riveli alternativamente il foro, sentirete chiaramente l’effetto della risonanza.
L’effetto 0,85r è ragionevole? Ra Inta, che ha fatto un dottorato di ricerca sull’acustica della chitarra nel nostro laboratorio, suggerisce una dimostrazione interessante:
Smorzate le corde della vostra chitarra in modo che non vibrino (per esempio un fazzoletto tra le corde e la tastiera). Tenete il palmo di una mano sopra la buca, e vicino ad essa. Con un dito dell’altra mano, dai un colpo secco alla tavola armonica vicino alla buca e alla prima corda. Sentirai un impulso d’aria sul palmo della tua mano. Il colpo del dito spinge la tavola armonica verso l’interno e spreme un po’ d’aria fuori dal corpo. Ora allontanate gradualmente la mano dalla buca e continuate a picchiettare con il dito. Quando smetti di sentire il movimento dell’aria? Questo vi darà una stima approssimativa della lunghezza dell'”effetto finale” nel caso della buca.
Tuning the Helmholtz resonance
Tra le pubblicazioni di John McLennan, uno studente di dottorato in questo laboratorio, c’è un articolo in cui varia la risonanza di Helmholtz variando la velocità del suono.
- McLennan, J.E. (2003) “Studi A0 e A1 sul violino usando CO2, He, e miscele aria/elio”. Acustica, 89, 176-180.
Alcune immagini di risonatori storici di Helmholtz fornite da Thomas B. Greenslade, Kenyon College, Ohio.
Leave a Reply