Articles /

Processo di Gram-Schmidt

di Marco Taboga, PhD

Il processo (o procedura) di Gram-Schmidt è una sequenza di operazioni che permettono di trasformare un insieme di vettori linearmente indipendenti in un insieme di vettori ortonormali che coprono lo stesso spazio dell’insieme originale.

Tabella del contenuto

Preliminari

Rivediamo alcune nozioni che sono essenziali per comprendere il processo di Gram-Schmidt.

Ricordiamo che due vettori $r$ e $s$ si dicono ortogonali se e solo se il loro prodotto interno è uguale a zero, cioè

Dato un prodotto interno, possiamo definire la norma (lunghezza) di un vettore $s$ come segue:

Un insieme di vettori è detto ortonormale se e solo se i suoi elementi hanno norma unitaria e sono ortogonali tra loro. In altre parole, un insieme di K vettori è ortonormale se e solo se

Abbiamo dimostrato che i vettori di un insieme ortonormale sono linearmente indipendenti.

Quando una base per uno spazio vettoriale è anche un insieme ortonormale, si chiama base ortonormale.

Proiezioni su insiemi ortonormali

Nel processo di Gram-Schmidt, usiamo ripetutamente la prossima proposizione, che mostra che ogni vettore può essere decomposto in due parti: 1) la sua proiezione su un insieme ortonormale e 2) un residuo che è ortogonale all’insieme ortonormale dato.

Proposizione Sia $S$ uno spazio vettoriale dotato di un prodotto interno . Sia un insieme ortonormale. Per qualsiasi $sin S$, abbiamodove $arepsilon _{S}$ è ortogonale a $u_{k}$ per qualsiasi $k=1,ldots ,K.$

Prova

DefinizioneQuindi, per ogni $j=1,ldots ,K$, abbiamo chedove: nei passi $rame{A}$ e $rame{B}$ abbiamo usato il fatto che il prodotto interno è lineare nel suo primo argomento; nel passo $rame{C}$ abbiamo usato il fatto che se $keq j$ poiché abbiamo a che fare con un insieme ortonormale; nel passo $rame{D}$ abbiamo usato il fatto che la norma di $u_{j}$ è uguale a 1. Pertanto, $arepsilon _{S}$, come definito sopra, è ortogonale a tutti gli elementi dell’insieme ortonormale, il che dimostra la proposizione.

Il termineè chiamato la proiezione lineare di $s$ sull’insieme ortonormale , mentre il termine $arepsilon _{S}$ è chiamato il residuo della proiezione lineare.

Normalizzazione

Un altro fatto forse ovvio che useremo ripetutamente nel processo di Gram-Schmidt è che, se prendiamo un qualsiasi vettore non nullo e lo dividiamo per la sua norma, allora il risultato della divisione è un nuovo vettore che ha norma unitaria.

In altre parole, se allora, per la proprietà di definitezza della norma, abbiamo che

Di conseguenza, possiamo definiree, per la positività e l’omogeneità assoluta della norma, abbiamo

Panoramica della procedura

Ora che sappiamo come normalizzare un vettore e come decomporlo in una proiezione su un insieme ortonormale e un residuo, siamo pronti per spiegare la procedura di Gram-Schmidt.

Daremo una panoramica del procedimento, dopo di che lo esprimeremo formalmente come una proposizione e discuteremo tutti i dettagli tecnici nella dimostrazione della proposizione.

Ecco la panoramica.

Ci viene dato un insieme di vettori linearmente indipendenti .

Per iniziare il processo, normalizziamo il primo vettore, cioè definiamo

Nel secondo passo, proiettiamo $s_{2}$ su $u_{1}$:dove $arepsilon _{2}$ è il residuo della proiezione.

Poi, normalizziamo il residuo:

Proveremo più tardi che (in modo che la normalizzazione possa essere eseguita) perché i vettori di partenza sono linearmente indipendenti.

I due vettori $u_{1}$ e $u_{2}$ così ottenuti sono ortonormali.

Nel terzo passo, proiettiamo $s_{3}$ su $u_{1}$ e $u_{2}$:e calcoliamo il residuo della proiezione $arepsilon _{3}$.

Poi lo normalizziamo:

Procediamo in questo modo fino ad ottenere l’ultimo residuo normalizzato $u_{K}$.

Alla fine del processo, i vettori formano un insieme ortonormale perché:

  1. sono il risultato di una normalizzazione, e di conseguenza hanno norma unitaria;

  2. ogni $u_{k}$ è ottenuto da un residuo che ha la proprietà di essere ortogonale a .

Per completare questa panoramica, ricordiamo che lo span lineare di è l’insieme di tutti i vettori che possono essere scritti come combinazioni lineari di ; è indicato con ed è uno spazio lineare.

Poiché i vettori sono combinazioni linearmente indipendenti di , ogni vettore che può essere scritto come combinazione lineare di può essere scritto anche come combinazione lineare di . Pertanto, gli span dei due insiemi di vettori coincidono:

Affermazione formale

Formalizziamo qui il processo di Gram-Schmidt come una proposizione, la cui dimostrazione contiene tutti i dettagli tecnici della procedura.

Proposizione Sia $S$ uno spazio vettoriale dotato di un prodotto interno . Che siano vettori linearmente indipendenti. Allora, esiste un insieme di vettori ortonormali tale cheper qualsiasi $kleq K$.

Prova

La prova è per induzione: prima proviamo che la proposizione è vera per $k=1$, e poi proviamo che è vera per un generico k se vale per $k-1$. Quando $k=1$, il vettoreha norma unitaria e costituisce da solo un insieme ortonormale: non ci sono altri vettori, quindi la condizione di ortogonalità è banalmente soddisfatta. L’insiemeè l’insieme di tutti i multipli scalari di $s_{1}$, che sono anche multipli scalari di $u_{1}$ (e viceversa). Quindi, Ora, supponiamo che la proposizione sia vera per $k-1$. Allora, possiamo proiettare $s_{k}$ su :dove il residuo $arepsilon _{k}$ è ortogonale a . Supponiamo che $arepsilon _{k}=0$. Allora,Siccome, per ipotesi, per qualsiasi $jleq k-1$, abbiamo che per qualsiasi $jleq k-1$, dove $lpha _{jl}$ sono scalari. Quindi,In altre parole, l’assunzione che $arepsilon _{k}=0$ porta alla conclusione che $s_{k}$ è una combinazione lineare di . Ma questo è impossibile perché una delle ipotesi della proposizione è che siano linearmente indipendenti. Di conseguenza, deve essere che . Possiamo quindi normalizzare il residuo e definire il vettoreche ha norma unitaria. Sappiamo già che $arepsilon _{k}$ è ortogonale a . Questo implica che anche $u_{k}$ è ortogonale a . Quindi, è un insieme ortonormale. Ora, prendiamo un qualsiasi vettore $sin S$ che può essere scritto comedove sono scalari. Poiché, per ipotesi, abbiamo che l’equazione (2) può anche essere scritta come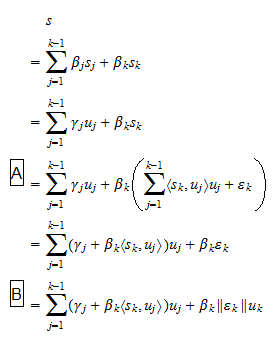dove sono scalari, e: nel passo $rame{A}$ abbiamo usato l’equazione (1); nel passo $rame{B}$ abbiamo usato la definizione di $u_{k}$. Così, abbiamo dimostrato che ogni vettore che può essere scritto come una combinazione lineare di può anche essere scritto come una combinazione lineare di . L’ipotesi (3) permette di provare il contrario in modo del tutto analogo: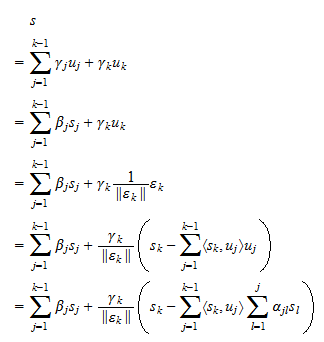In altre parole, ogni combinazione lineare di è anche una combinazione lineare di . Questo dimostra che e conclude la dimostrazione.

Ogni spazio a prodotto interno ha una base ortonormale

La seguente proposizione presenta un’importante conseguenza del processo di Gram-Schmidt.

Proposizione Sia $S$ uno spazio vettoriale dotato di un prodotto interno . Se $S$ ha dimensione finita , allora esiste una base ortonormale per $S$.

Prova

Siccome $S$ è a dimensione finita, esiste almeno una base per $S$, costituita da K vettori . Possiamo applicare la procedura di Gram-Schmidt alla base e ottenere un insieme ortonormale . Poiché è una base, essa si estende su $S$. Pertanto, 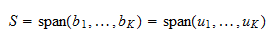Quindi, è una base ortonormale di $S$.

Esercizi risolti

Di seguito puoi trovare alcuni esercizi con soluzioni spiegate.

Esercizio 1

Consideriamo lo spazio $S$ di tutti i $3imes 1$ vettori aventi entrate reali e il prodotto internodove $r,sin S$ e $s^{op }$ è la trasposizione di $s$. Definire il vettore

Normalizzare $s$.

Soluzione

La norma di $s$ èQuindi, la normalizzazione di $s$ è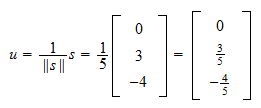

Esercizio 2

Consideriamo lo spazio $S$ di tutti i $2imes 1$ vettori con entrate reali e il prodotto internodove $r,sin S$ . Consideriamo i due vettori linearmente indipendenti

Trasformarli in un insieme ortonormale utilizzando il processo di Gram-Schmidt.

Soluzione

La norma di $s_{1}$ è Quindi, il primo vettore ortonormale èIl prodotto interno di $s_{2}$ e $u_{1}$ è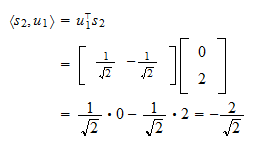La proiezione di $s_{2}$ su $u_{1}$ è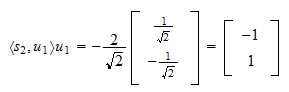Il residuo della proiezione è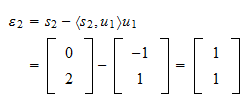La norma del residuo èe il residuo normalizzato èQuindi, l’insieme ortonormale che stavamo cercando è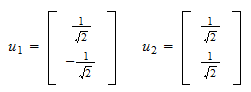

Come citare

Cita come:

Taboga, Marco (2017). “Processo di Gram-Schmidt”, Lezioni di algebra matriciale. https://www.statlect.com/matrix-algebra/Gram-Schmidt-process.

Leave a Reply